人教版七年级下册 9.1.2 不等式的性质 课件(共40张PPT)
文档属性
| 名称 | 人教版七年级下册 9.1.2 不等式的性质 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 17:14:48 | ||
图片预览







文档简介
(共40张PPT)
9.1.2 不等式的性质
人教版七年级《数学》下册
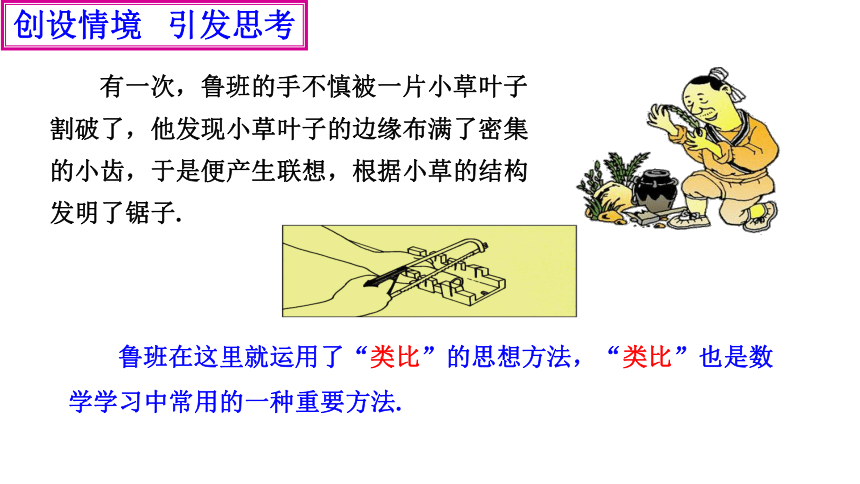
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
创设情境 引发思考
1.请直接说出不等式的解集:
(1) x+3>6 (2)2x<8
思考:(1)你还能直接说出下面不等式的解集吗?
思考:(2)你还会解下面的一元一次方程吗?
创设情境 引发思考
解一元一次方程:
解:去分母,得 2(5x+1)-24=3(x-5)
去括号,得 10x+2-24=3x-15
移项,得10x-3x=-15+24-2
合并,得7x=7
系数化为1,得x=1
依据
等式性质2
等式性质1
等式性质2
分配律(去括号法则)
分配律逆运算(合并同类项法则)
思考回顾 唤醒记忆
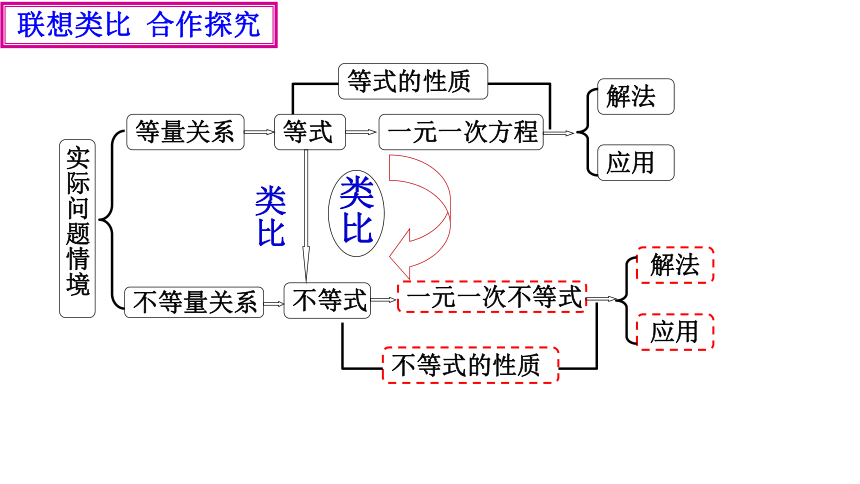
等量关系
等式
解法
实际问题情境
不等式
一元一次不等式
一元一次方程
不等量关系
应用
等式的性质
不等式的性质
解法
应用
类比
类比
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
和等式的性质1类比,你能提出一个怎样的问题?
等式的性质1:
等式两边加(或减去)同一个数 (或式子),结果仍相等.
如果a=b,那么 a±c=b ± c
联想类比 合作探究
和等式的性质2类比,你能提出一个怎样的问题?
等式性质2:
等式两边乘同一个数 ,或除以同一个不为0的数,结果仍相等.
如果a=b, 那么ac=bc;
如果a=b(c≠0),那么 .
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
要求:自己想出一些数,在“□”内按要求填上数字,在“ ”上填
上“>”“<”或“=”号,仔细观察,发现规律.
不等式 两边加上同一个数 两边减去同一个数
5>3 5+□ 3+□ 5-□ 3-□
5+□ 3+□ 5-□ 3-□
5+□ 3+□ 5-□ 3-□
-1<3 -1+□ 3+□ -1-□ 3-□
-1+□ 3+□ -1-□ 3-□
-1+□ 3+□ -1-□ 3-□
自主设计 结论 4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
>
>
>
>
>
>
<
<
<
<
<
<
-2>-5
-2+3>-5+3
-2-4>-5-4
实验探究
不等式 两边加上同一个数 两边减去同一个数
6>2 6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
-2<3 -2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
自主设计 结论 2
2
4
4
0
-4
>
<
0
-4
2
2
4
4
0
0
-4
-4
2
2
4
4
0(无意义)
-4
0
-4
2
2
4
4
0(无意义)
-4
0
-4
>
=
<
<
=
>
>
<
>
<
<
>
-4>-6
-2×2>-6×2
-2÷2>-6÷2
-4>-6
-2×(-2) <-6×(-2)
-2÷(-2)<-6÷(-2)
实验探究
即:如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b,那么a+c<b+c,a-c<b-c.
你能举几个生活中具体的实例说明不等式的性质1吗?
类比归纳 形成概念
不等式的性质1:
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
把a>b表示在数轴上,不妨设c>0
b
b+c
a
a+c
b
b-c
a
a-c
∴a+c>b+c.
∴a-c>b-c.
同理可得当c<0时, a+c>b+c,a-c>b-c.
不等式的性质1
如果a>b,那么a±c>b±c.
类比归纳 形成概念
思考:对于不等式a>b,当c=0时,ac___bc.
不等式的性质2:
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,且c>0,那么ac>bc或 .
=
不等式的性质3:
不等式的两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc或 .
类比归纳 形成概念
不等式的性质 等式的性质
性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变; 性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变; 性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变. 性质1 等式两边加(或减)同一个数(或式子),结果仍相等.
性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
不等式的性质与等式的性质有什么相同点和不同点?
类比概念 感悟新知
(1) 3a____3b;
(2) a-8____b-8;
(3) -2a____-2b;
(4)-3.5a+1 -3.5b+1;
>
<
>
<
1.设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质.
不等式性质3
不等式性质3、1
不等式性质2
不等式性质1
初步应用 感受新知
(1)
(2)
(3)
(4)
>
<
<
>
变式:若 a>b ,c<0,用“<”或“>”填空,并说明依据不等式的哪条性质.
不等式性质2、1
不等式性质2
不等式性质3
不等式性质3、1
初步应用 感受新知
例1 利用不等式的性质解下列不等式.
(1)x-7>26 (2)3x<2x+1
(3)- x > 50 (4)-4x > 3
3
2
学以致用 强化新知
解未知数为x的不等式
化为x>a或x<a的形式
目标
方法:不等式基本性质1~3
思路:
(1) x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x>a或x<a的形式.
这个不等式的解集在数轴上的表示如图,
0
33
解:根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7>26+7,
x>33.
(2) 3x<2x+1
3x-2x<2x+1-2x
x<1
解:根据 ,不等式两边都 ,不等号的方向 ,得
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
0
1
不等式的性质1
减去2x
不变
x>75
这个不等式的解集在数轴的表示如图
0
75
解:根据 ,不等式的两边都 , 不等号的方向不变,得
(3)
不等式的性质2
3
2
乘 -
(4)-4x>3
解:根据 ,不等式两边都除以 ,不等号的方向 ,得
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向.
-
4
3
0
不等式的性质3
-4
改变
下面是某同学根据不等式的性质做的一道题:
在不等式-4x+5>9的两边都减去5,得
-4x>4
在不等式-4x>4的两边都除以-4,得
x>-1
请问他做对了吗?如果不对,请改正.
不对
x<-1
学以致用 强化新知
1.某长方体形状容器长5 cm,宽3 cm,高10 cm. 容器内原有水的高度为3 cm. 现准备继续向它注水,用V(单位:cm3 )表示新注入水的体积,写出V的取值范围.
分析:本题的不等关系是什么?
原有水的体积+新注入的水的体积<长方形的体积.
学以致用 强化新知
1.某长方体形状容器长5 cm,宽3 cm,高10 cm. 容器内原有水的高度为3 cm. 现准备继续向它注水,用V(单位:cm3 )表示新注入水的体积,写出V的取值范围.
V+3×5×3 ≤3×5×10,V ≤105.
有由于新注入水的体积V不能为负数,
因此,V的取值范围是 : V ≥0并且V ≤105.
在数轴上表示V的取值范围
0
105
学以致用 强化新知
解:3x≥1, 解集是x≥
x+3≥6, 解集是x≥3
y-1≤0,解集是y ≤1
0
3
0
1
0
-8
0
y≤-2,解集是y≤-8
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集.
学以致用 强化新知
3. 试比较2a与a的大小.
解法1:∵2>1,a<0,
∴2a<a(不等式的性质3)
解法2: 在数轴上分别表示2a和a的点(a<0),如图. 2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
当a<0时 ,
分类讨论
学以致用 强化新知
解法3:
∵a<0,
∴ a+a<0+a,
即2a <a.
解法4:
∵2a-a=a ,而a<0
∴2a-a<0. ∴2a<a
思考:当a>0时呢?当a=0时呢?
(不等式的性质2)
(不等式基本性质2)
作差法
分类讨论
3. 试比较2a与a的大小.
学以致用 强化新知
回顾这节课的学习过程,请同学们谈谈收获?
知识内容
利用不等式的性质解不等式
思想方法
化归
数形结合
类比方程的学习
知识梳理 自我构建
追问 你认为接下来要研究哪些内容?应该如何展开?
研究思路
分类讨论
不等式的应用
类比
你对方程、不等式的知识体系是否有更加深刻的认识了呢?
整体构建 完善体系
一元一次不等式
一元一次不等式组
应用
概念
不等式的解(集)
解不等式
方程
不等式
概念
方程的解
解方程
应用
类比
类比
类比
……
一元一次方程
二元一次方程(组)
类比
等式的性质
不等式的性质
回顾这节课的学习过程,请同学们谈谈收获?
1.已知a>b,用“<”或“>”号填空:
① a+2 b+2; ② a-3 b-3;
③ -4a -4b; ④ .
2.(1)若x+1>0,两边同加上-1,得_________,
依据_______________.
(2)若2 x<-6,两边同除以2,得________,
依据_______________.
(3)若-2x≤6,两边同除以-2,得_______,
依据 .
课堂检测
>
>
>
<
x>-1
x<-3
x>-3
不等式性质3
不等式性质2
不等式性质1
3. 若m>n,则下列各式中不一定的是( )
A. m-2>n-2 B. 2m>2n
C. -2m>-2n D.
C
课堂检测
4.利用不等式的性质解下列不等式.
(1)x+5>-1 (2)4x<3x-5
(3)- x<- (4)-8x>10
7
1
7
6
(1)x >-6 (2)x <-5
(3) x<6 (4)x<-1.25
课堂检测
5.(1)若由x>y,得ax>ay,则a ___0;
(2)若由x>y,得ax<ay,则a ___0.
>
<
课堂检测
6.小希就读的学校上午第一节课上课时间是8 点开始.小希家距学校有2 千米,而她的步行速度为每小时10 千米. 那么,小希上午几点从家里出发才能保证不迟到?
解:设小希上午x 点从家里出发才能不迟到,根据题意得
答:小希上午7:48前时从家里出发才能不迟到.
≤8
解得x≤
课堂检测
9.1.2 不等式的性质
人教版七年级《数学》下册
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
创设情境 引发思考
1.请直接说出不等式的解集:
(1) x+3>6 (2)2x<8
思考:(1)你还能直接说出下面不等式的解集吗?
思考:(2)你还会解下面的一元一次方程吗?
创设情境 引发思考
解一元一次方程:
解:去分母,得 2(5x+1)-24=3(x-5)
去括号,得 10x+2-24=3x-15
移项,得10x-3x=-15+24-2
合并,得7x=7
系数化为1,得x=1
依据
等式性质2
等式性质1
等式性质2
分配律(去括号法则)
分配律逆运算(合并同类项法则)
思考回顾 唤醒记忆
等量关系
等式
解法
实际问题情境
不等式
一元一次不等式
一元一次方程
不等量关系
应用
等式的性质
不等式的性质
解法
应用
类比
类比
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
和等式的性质1类比,你能提出一个怎样的问题?
等式的性质1:
等式两边加(或减去)同一个数 (或式子),结果仍相等.
如果a=b,那么 a±c=b ± c
联想类比 合作探究
和等式的性质2类比,你能提出一个怎样的问题?
等式性质2:
等式两边乘同一个数 ,或除以同一个不为0的数,结果仍相等.
如果a=b, 那么ac=bc;
如果a=b(c≠0),那么 .
联想类比 合作探究
联想类比 合作探究
联想类比 合作探究
要求:自己想出一些数,在“□”内按要求填上数字,在“ ”上填
上“>”“<”或“=”号,仔细观察,发现规律.
不等式 两边加上同一个数 两边减去同一个数
5>3 5+□ 3+□ 5-□ 3-□
5+□ 3+□ 5-□ 3-□
5+□ 3+□ 5-□ 3-□
-1<3 -1+□ 3+□ -1-□ 3-□
-1+□ 3+□ -1-□ 3-□
-1+□ 3+□ -1-□ 3-□
自主设计 结论 4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
4
4
0
0
-2
-2
>
>
>
>
>
>
<
<
<
<
<
<
-2>-5
-2+3>-5+3
-2-4>-5-4
实验探究
不等式 两边加上同一个数 两边减去同一个数
6>2 6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
6×□ 2×□ 6÷□ 2÷□
-2<3 -2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
-2×□ 3×□ -2÷□ 3÷□
自主设计 结论 2
2
4
4
0
-4
>
<
0
-4
2
2
4
4
0
0
-4
-4
2
2
4
4
0(无意义)
-4
0
-4
2
2
4
4
0(无意义)
-4
0
-4
>
=
<
<
=
>
>
<
>
<
<
>
-4>-6
-2×2>-6×2
-2÷2>-6÷2
-4>-6
-2×(-2) <-6×(-2)
-2÷(-2)<-6÷(-2)
实验探究
即:如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b,那么a+c<b+c,a-c<b-c.
你能举几个生活中具体的实例说明不等式的性质1吗?
类比归纳 形成概念
不等式的性质1:
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
把a>b表示在数轴上,不妨设c>0
b
b+c
a
a+c
b
b-c
a
a-c
∴a+c>b+c.
∴a-c>b-c.
同理可得当c<0时, a+c>b+c,a-c>b-c.
不等式的性质1
如果a>b,那么a±c>b±c.
类比归纳 形成概念
思考:对于不等式a>b,当c=0时,ac___bc.
不等式的性质2:
不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,且c>0,那么ac>bc或 .
=
不等式的性质3:
不等式的两边乘(或除以)同一个负数,不等号的方向改变.
如果a>b,且c<0,那么ac<bc或 .
类比归纳 形成概念
不等式的性质 等式的性质
性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变; 性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变; 性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变. 性质1 等式两边加(或减)同一个数(或式子),结果仍相等.
性质2 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
不等式的性质与等式的性质有什么相同点和不同点?
类比概念 感悟新知
(1) 3a____3b;
(2) a-8____b-8;
(3) -2a____-2b;
(4)-3.5a+1 -3.5b+1;
>
<
>
<
1.设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质.
不等式性质3
不等式性质3、1
不等式性质2
不等式性质1
初步应用 感受新知
(1)
(2)
(3)
(4)
>
<
<
>
变式:若 a>b ,c<0,用“<”或“>”填空,并说明依据不等式的哪条性质.
不等式性质2、1
不等式性质2
不等式性质3
不等式性质3、1
初步应用 感受新知
例1 利用不等式的性质解下列不等式.
(1)x-7>26 (2)3x<2x+1
(3)- x > 50 (4)-4x > 3
3
2
学以致用 强化新知
解未知数为x的不等式
化为x>a或x<a的形式
目标
方法:不等式基本性质1~3
思路:
(1) x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x>a或x<a的形式.
这个不等式的解集在数轴上的表示如图,
0
33
解:根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7>26+7,
x>33.
(2) 3x<2x+1
3x-2x<2x+1-2x
x<1
解:根据 ,不等式两边都 ,不等号的方向 ,得
这个不等式的解在数轴上的表示如图
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
0
1
不等式的性质1
减去2x
不变
x>75
这个不等式的解集在数轴的表示如图
0
75
解:根据 ,不等式的两边都 , 不等号的方向不变,得
(3)
不等式的性质2
3
2
乘 -
(4)-4x>3
解:根据 ,不等式两边都除以 ,不等号的方向 ,得
这个不等式的解集在数轴上的表示如图
注意:(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向.
-
4
3
0
不等式的性质3
-4
改变
下面是某同学根据不等式的性质做的一道题:
在不等式-4x+5>9的两边都减去5,得
-4x>4
在不等式-4x>4的两边都除以-4,得
x>-1
请问他做对了吗?如果不对,请改正.
不对
x<-1
学以致用 强化新知
1.某长方体形状容器长5 cm,宽3 cm,高10 cm. 容器内原有水的高度为3 cm. 现准备继续向它注水,用V(单位:cm3 )表示新注入水的体积,写出V的取值范围.
分析:本题的不等关系是什么?
原有水的体积+新注入的水的体积<长方形的体积.
学以致用 强化新知
1.某长方体形状容器长5 cm,宽3 cm,高10 cm. 容器内原有水的高度为3 cm. 现准备继续向它注水,用V(单位:cm3 )表示新注入水的体积,写出V的取值范围.
V+3×5×3 ≤3×5×10,V ≤105.
有由于新注入水的体积V不能为负数,
因此,V的取值范围是 : V ≥0并且V ≤105.
在数轴上表示V的取值范围
0
105
学以致用 强化新知
解:3x≥1, 解集是x≥
x+3≥6, 解集是x≥3
y-1≤0,解集是y ≤1
0
3
0
1
0
-8
0
y≤-2,解集是y≤-8
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
2. 用不等式表示下列语句并写出解集,并在数轴上表示解集.
学以致用 强化新知
3. 试比较2a与a的大小.
解法1:∵2>1,a<0,
∴2a<a(不等式的性质3)
解法2: 在数轴上分别表示2a和a的点(a<0),如图. 2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
当a<0时 ,
分类讨论
学以致用 强化新知
解法3:
∵a<0,
∴ a+a<0+a,
即2a <a.
解法4:
∵2a-a=a ,而a<0
∴2a-a<0. ∴2a<a
思考:当a>0时呢?当a=0时呢?
(不等式的性质2)
(不等式基本性质2)
作差法
分类讨论
3. 试比较2a与a的大小.
学以致用 强化新知
回顾这节课的学习过程,请同学们谈谈收获?
知识内容
利用不等式的性质解不等式
思想方法
化归
数形结合
类比方程的学习
知识梳理 自我构建
追问 你认为接下来要研究哪些内容?应该如何展开?
研究思路
分类讨论
不等式的应用
类比
你对方程、不等式的知识体系是否有更加深刻的认识了呢?
整体构建 完善体系
一元一次不等式
一元一次不等式组
应用
概念
不等式的解(集)
解不等式
方程
不等式
概念
方程的解
解方程
应用
类比
类比
类比
……
一元一次方程
二元一次方程(组)
类比
等式的性质
不等式的性质
回顾这节课的学习过程,请同学们谈谈收获?
1.已知a>b,用“<”或“>”号填空:
① a+2 b+2; ② a-3 b-3;
③ -4a -4b; ④ .
2.(1)若x+1>0,两边同加上-1,得_________,
依据_______________.
(2)若2 x<-6,两边同除以2,得________,
依据_______________.
(3)若-2x≤6,两边同除以-2,得_______,
依据 .
课堂检测
>
>
>
<
x>-1
x<-3
x>-3
不等式性质3
不等式性质2
不等式性质1
3. 若m>n,则下列各式中不一定的是( )
A. m-2>n-2 B. 2m>2n
C. -2m>-2n D.
C
课堂检测
4.利用不等式的性质解下列不等式.
(1)x+5>-1 (2)4x<3x-5
(3)- x<- (4)-8x>10
7
1
7
6
(1)x >-6 (2)x <-5
(3) x<6 (4)x<-1.25
课堂检测
5.(1)若由x>y,得ax>ay,则a ___0;
(2)若由x>y,得ax<ay,则a ___0.
>
<
课堂检测
6.小希就读的学校上午第一节课上课时间是8 点开始.小希家距学校有2 千米,而她的步行速度为每小时10 千米. 那么,小希上午几点从家里出发才能保证不迟到?
解:设小希上午x 点从家里出发才能不迟到,根据题意得
答:小希上午7:48前时从家里出发才能不迟到.
≤8
解得x≤
课堂检测
