2022--2023学年青岛版七年级数学下册期末巩固训练试题(含答案)
文档属性
| 名称 | 2022--2023学年青岛版七年级数学下册期末巩固训练试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 23:16:48 | ||
图片预览


文档简介
2022--2023学年青岛版七年级数学下册期末巩固训练试题
一、单选题
1.下列各式中,计算结果为 的是( )
A. B. C. D.
2.若 ,则化简 的结果为( )
A.3 B.-3 C. D.
3.一个三角形的两边长分别是3和7,则第三边长可能是( )
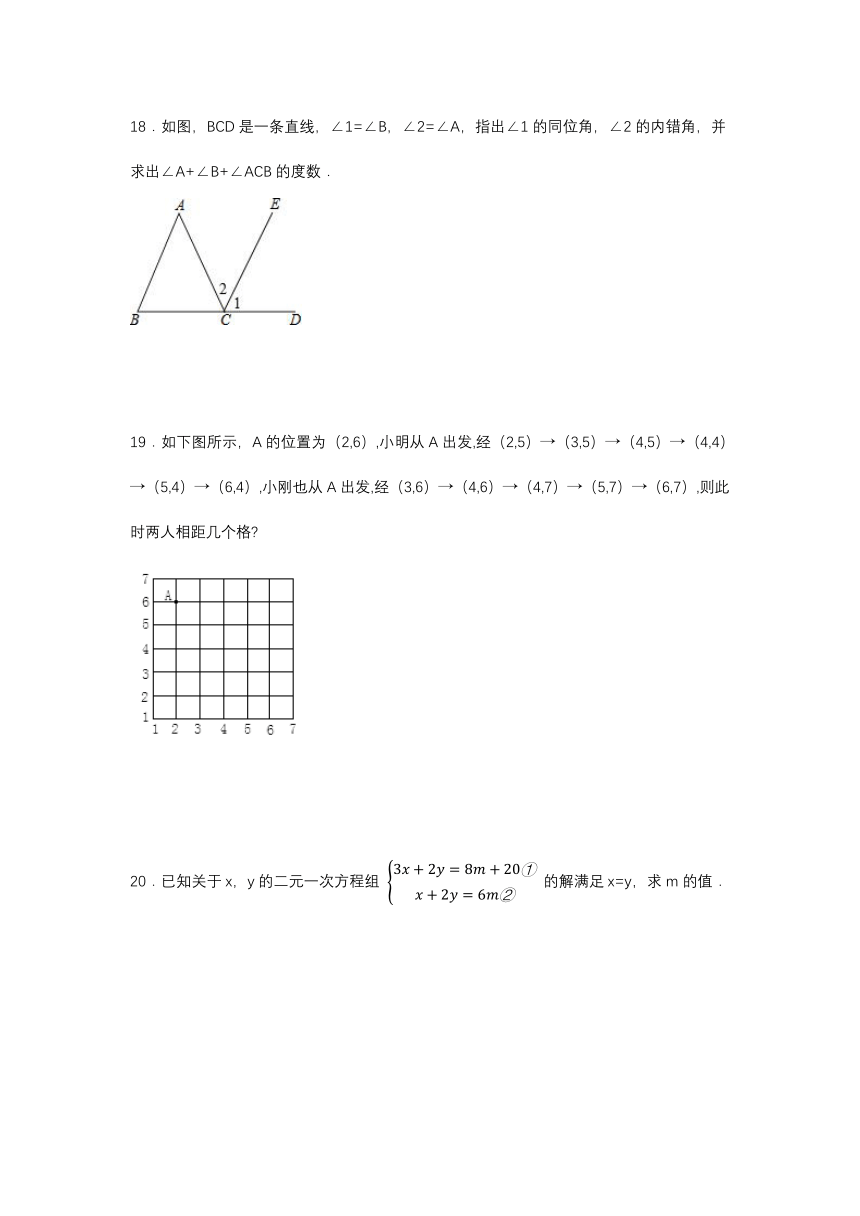
A.2 B.3 C.9 D.10
4.某工程队计划把河水引到水池A中,他们先过A点作,垂足为B,CD为河岸,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
A.两点之间的所有连线中,线段最短
B.过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
5.若方程组 的解是 ,则方程组 的解是( )
A. B.
C. D.
6.如图,点 在 的延长线上,下列条件中能判断 的是( )
A. B.
C. D.
7.如图,用尺规作出了,关于作图痕迹,下列说法错误的是( )
A.弧是以点O为圆心,任意长为半径的弧
B.弧是以点C为圆心,为半径的弧
C.弧是以点E为圆心,为半径的弧
D.弧是以点E为圆心,为半径的弧
8.如果三角形的一个外角与它不相邻的两个内角的和为 ,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
9.《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B.
C. D.
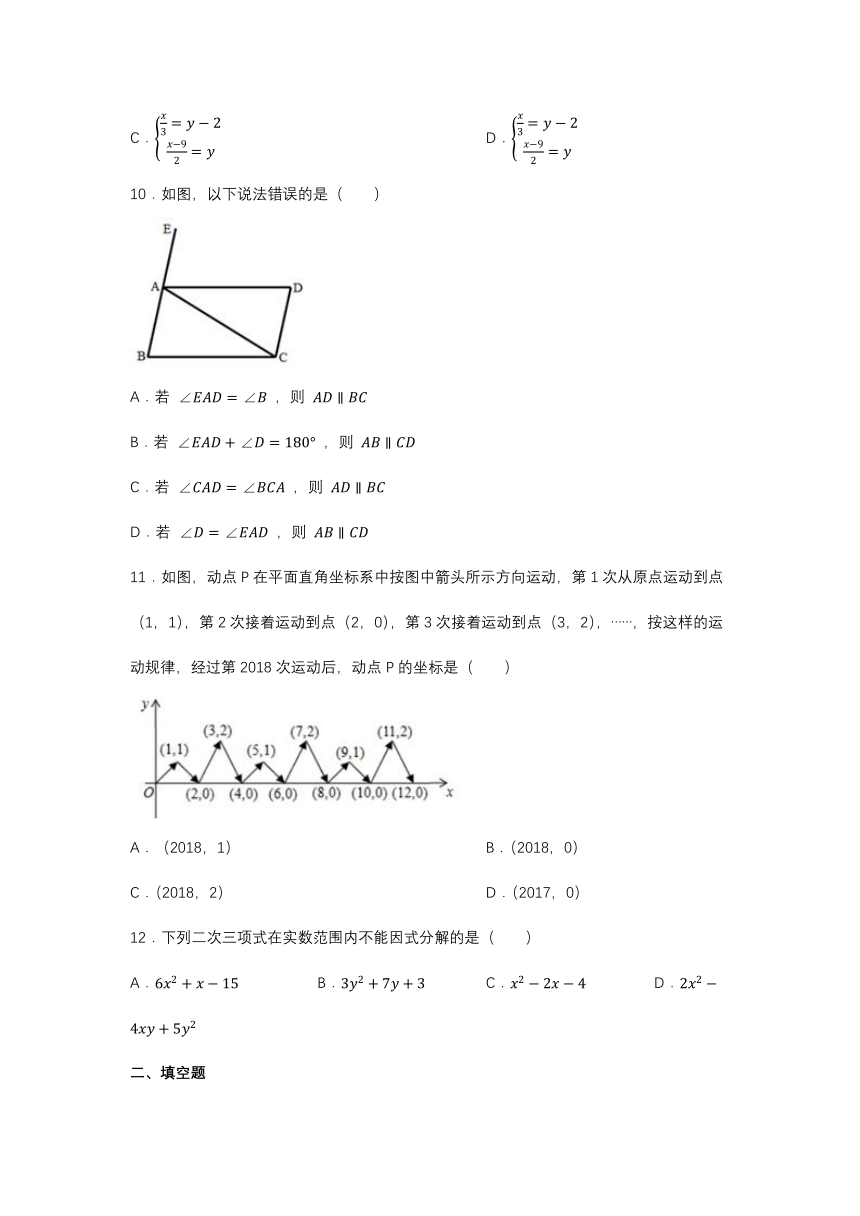
10.如图,以下说法错误的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
11.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2018次运动后,动点P的坐标是( )
(2018,1) B.(2018,0)
C.(2018,2) D.(2017,0)
12.下列二次三项式在实数范围内不能因式分解的是( )
A. B. C. D.
二、填空题
13.在平面直角坐标系中,若点A的坐标为(8,4),则点A到y轴的距离为 .
14.如图, 中, 是 上一点, 是 上一点, , , ,则 .
15.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= .
16.如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为 .
三、解答题
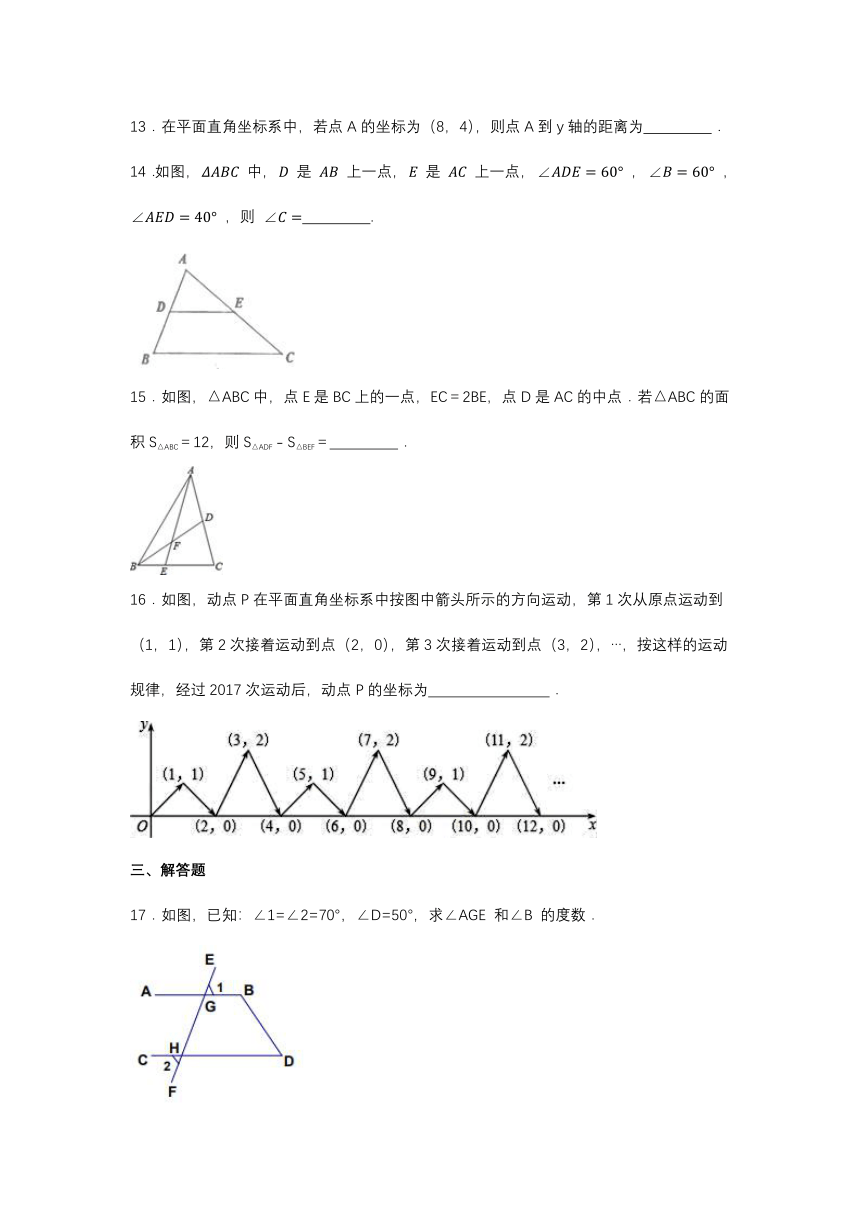
17.如图,已知:∠1=∠2=70°,∠D=50°,求∠AGE 和∠B 的度数.
18.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
19.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
20.已知关于x,y的二元一次方程组 的解满足x=y,求m的值.
21.如图,AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE
22.如图,AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠1+∠2=180°.∠CGD与∠BAC相等吗?为什么?
23.如图,在四边形ABCD中,AB∥CD,点P为BC上一点(点P与B,C不重合),设∠CDP=∠α,∠CPD=∠β,你能不能说明,不论点P在BC上怎样运动,总有∠α+∠β=∠B.
24.k为正整数,已知关于x,y的二元一次方程组 有整数解,求2k+x+y的平方根。
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】B
12.【答案】D
13.【答案】8
14.【答案】40
15.【答案】2
16.【答案】(2017,1)
17.【答案】解:∵∠1=∠2=70°,
∴∠AGE=180°-∠1=110°,∠AGF=∠1=70°
∴∠2=∠AGF
∴AB∥CD
∴∠B+∠D=180°
∵∠D=50°
∴∠B=180°-∠D=130°
18.【答案】解:得∠1的同位角是∠B,∠2的内错角∠A,
∵ ∠1=∠B,∠2=∠A ,
∴ ∠A+∠B+∠ACB=∠ACB+∠1+∠2=180° 。
19.【答案】解:如下图所示,可知小明与小刚相距3个格.
20.【答案】解:∵关于x,y的二元一次方程组 的解满足x=y,
∴ ,
故 2m,
解得:m=10.
21.【答案】解:∵AB∥CD(已知)
∴∠4=∠EAB(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠EAB(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAE=∠CAD(角的和差)
∴∠3=∠CAD.
∴AD∥BE (内错角相等,两直线平行).
22.【答案】解:∠CGD=∠BAC,
理由是:∵AD是△ABC的高,EF⊥BC,
∴∠ADB=∠EFB=90°,
∴AD∥EF,
∴∠2+∠BAD=180°,
∵∠1+∠2=180°,
∴∠1=∠BAD,
∴DG∥AB,
∴∠CGD=∠BAC
23.【答案】解:过点P作PE∥CD交AD于E,则∠DPE=∠α.
∵AB∥CD,∴PE∥AB.
∴∠CPE=∠B,即∠DPE+∠β=∠α+∠β=∠B.故不论点P在BC上怎样运动,总有∠α+∠β=∠B
24.【答案】解:①+② 得 (3+ ) =10 =
∵ 为正整数,∴3+ =±1,±2,±5,±10
∴ 为7或2
当 =2时, = =2 = =3
当 =7时, =1 = (舍)
∴± =±3
一、单选题
1.下列各式中,计算结果为 的是( )
A. B. C. D.
2.若 ,则化简 的结果为( )
A.3 B.-3 C. D.
3.一个三角形的两边长分别是3和7,则第三边长可能是( )
A.2 B.3 C.9 D.10
4.某工程队计划把河水引到水池A中,他们先过A点作,垂足为B,CD为河岸,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
A.两点之间的所有连线中,线段最短
B.过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
5.若方程组 的解是 ,则方程组 的解是( )
A. B.
C. D.
6.如图,点 在 的延长线上,下列条件中能判断 的是( )
A. B.
C. D.
7.如图,用尺规作出了,关于作图痕迹,下列说法错误的是( )
A.弧是以点O为圆心,任意长为半径的弧
B.弧是以点C为圆心,为半径的弧
C.弧是以点E为圆心,为半径的弧
D.弧是以点E为圆心,为半径的弧
8.如果三角形的一个外角与它不相邻的两个内角的和为 ,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
9.《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B.
C. D.
10.如图,以下说法错误的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
11.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),……,按这样的运动规律,经过第2018次运动后,动点P的坐标是( )
(2018,1) B.(2018,0)
C.(2018,2) D.(2017,0)
12.下列二次三项式在实数范围内不能因式分解的是( )
A. B. C. D.
二、填空题
13.在平面直角坐标系中,若点A的坐标为(8,4),则点A到y轴的距离为 .
14.如图, 中, 是 上一点, 是 上一点, , , ,则 .
15.如图,△ABC中,点E是BC上的一点,EC=2BE,点D是AC的中点.若△ABC的面积S△ABC=12,则S△ADF﹣S△BEF= .
16.如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为 .
三、解答题
17.如图,已知:∠1=∠2=70°,∠D=50°,求∠AGE 和∠B 的度数.
18.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
19.如下图所示,A的位置为(2,6),小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格
20.已知关于x,y的二元一次方程组 的解满足x=y,求m的值.
21.如图,AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE
22.如图,AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠1+∠2=180°.∠CGD与∠BAC相等吗?为什么?
23.如图,在四边形ABCD中,AB∥CD,点P为BC上一点(点P与B,C不重合),设∠CDP=∠α,∠CPD=∠β,你能不能说明,不论点P在BC上怎样运动,总有∠α+∠β=∠B.
24.k为正整数,已知关于x,y的二元一次方程组 有整数解,求2k+x+y的平方根。
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】B
12.【答案】D
13.【答案】8
14.【答案】40
15.【答案】2
16.【答案】(2017,1)
17.【答案】解:∵∠1=∠2=70°,
∴∠AGE=180°-∠1=110°,∠AGF=∠1=70°
∴∠2=∠AGF
∴AB∥CD
∴∠B+∠D=180°
∵∠D=50°
∴∠B=180°-∠D=130°
18.【答案】解:得∠1的同位角是∠B,∠2的内错角∠A,
∵ ∠1=∠B,∠2=∠A ,
∴ ∠A+∠B+∠ACB=∠ACB+∠1+∠2=180° 。
19.【答案】解:如下图所示,可知小明与小刚相距3个格.
20.【答案】解:∵关于x,y的二元一次方程组 的解满足x=y,
∴ ,
故 2m,
解得:m=10.
21.【答案】解:∵AB∥CD(已知)
∴∠4=∠EAB(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠EAB(等量代换)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAE=∠CAD(角的和差)
∴∠3=∠CAD.
∴AD∥BE (内错角相等,两直线平行).
22.【答案】解:∠CGD=∠BAC,
理由是:∵AD是△ABC的高,EF⊥BC,
∴∠ADB=∠EFB=90°,
∴AD∥EF,
∴∠2+∠BAD=180°,
∵∠1+∠2=180°,
∴∠1=∠BAD,
∴DG∥AB,
∴∠CGD=∠BAC
23.【答案】解:过点P作PE∥CD交AD于E,则∠DPE=∠α.
∵AB∥CD,∴PE∥AB.
∴∠CPE=∠B,即∠DPE+∠β=∠α+∠β=∠B.故不论点P在BC上怎样运动,总有∠α+∠β=∠B
24.【答案】解:①+② 得 (3+ ) =10 =
∵ 为正整数,∴3+ =±1,±2,±5,±10
∴ 为7或2
当 =2时, = =2 = =3
当 =7时, =1 = (舍)
∴± =±3
同课章节目录
