八年级数学上册试题 6.3从统计图分析数据的集中趋势-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 6.3从统计图分析数据的集中趋势-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 09:04:13 | ||
图片预览



文档简介
6.3从统计图分析数据的集中趋势
一、选择题
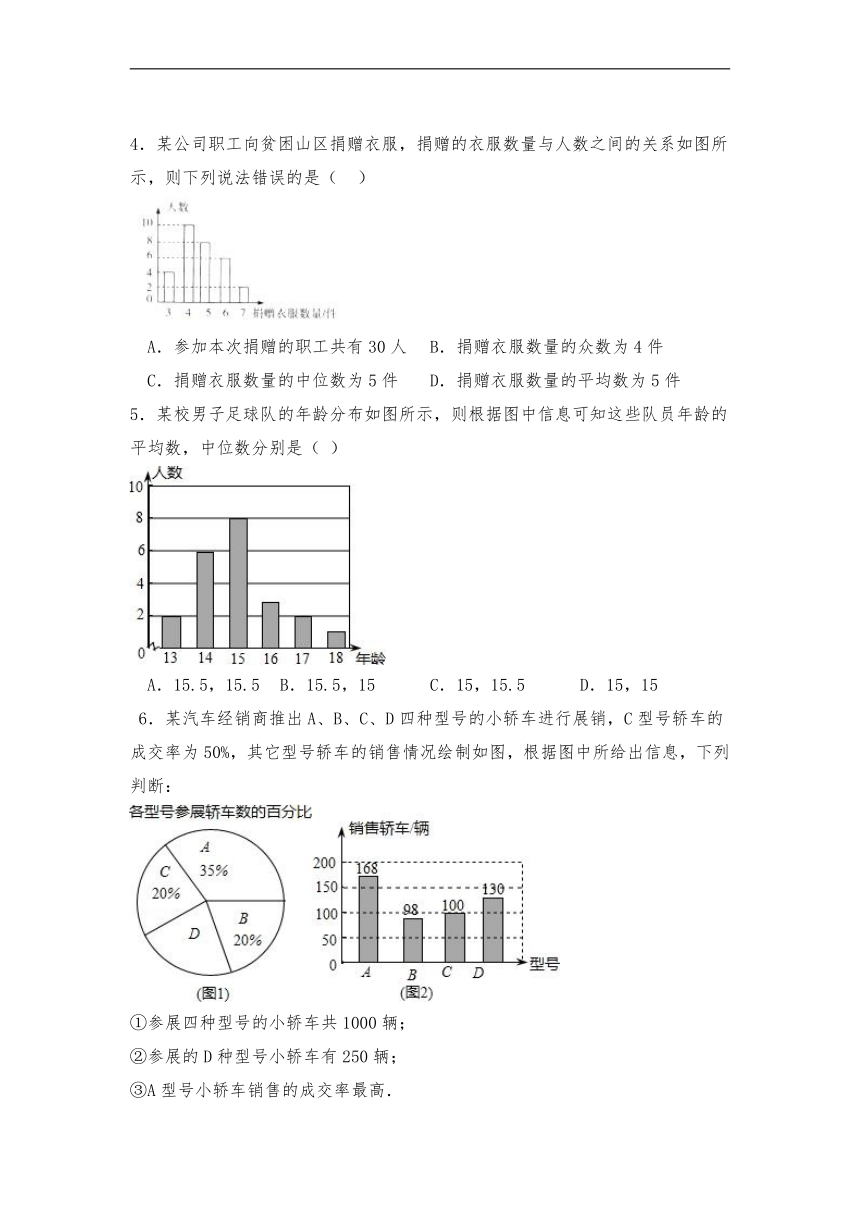
1. 某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A. 4 B. 3 C. 2 D. 1
2. 如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A. 16,10.5 B. 8,9 C. 16,8.5 D. 8,8.5
3. 如图是我市6月份某7天的最高气温折线统计图,则这些最高气温的众数与中位数分别是()
A. 26,30°C B. 28°C,27°C
C. 28°C,28°C D. 27°C,28°C
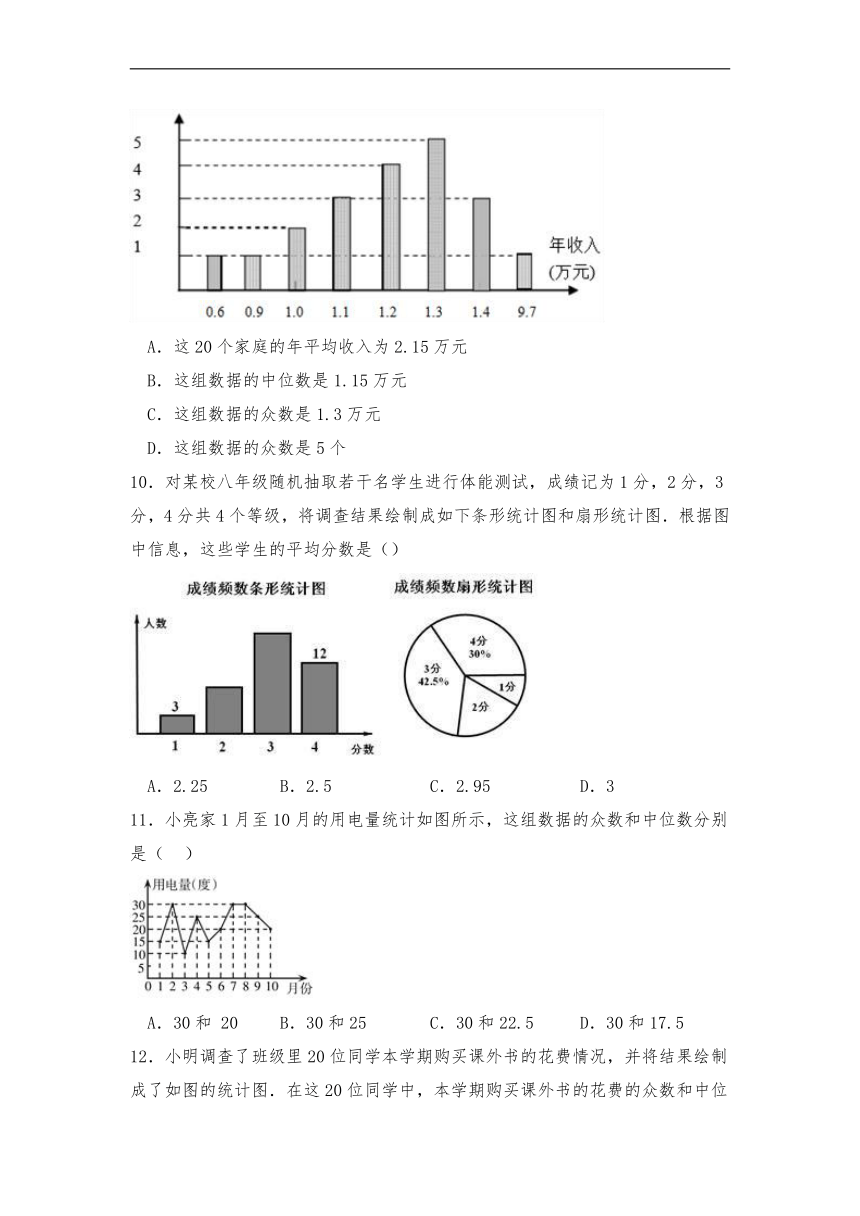
4.某公司职工向贫困山区捐赠衣服,捐赠的衣服数量与人数之间的关系如图所示,则下列说法错误的是( )
A.参加本次捐赠的职工共有30人 B.捐赠衣服数量的众数为4件
C.捐赠衣服数量的中位数为5件 D.捐赠衣服数量的平均数为5件
5.某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
A.15.5,15.5 B.15.5,15 C.15,15.5 D.15,15
6.某汽车经销商推出A、B、C、D四种型号的小轿车进行展销,C型号轿车的成交率为50%,其它型号轿车的销售情况绘制如图,根据图中所给出信息,下列判断:
①参展四种型号的小轿车共1000辆;
②参展的D种型号小轿车有250辆;
③A型号小轿车销售的成交率最高.
其中正确的判断有( )
A.0个 B.1个 C.2个 D.3个
7.某班班长统计去年1 8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50
B.众数是42
C.中位数是58
D.每月阅读数量超过40的有4个月
8.甲、乙两名队员参加射击训练,并将他们的射击成绩分别制作成如图所示的两个统计图:
下列说法中错误的是( )
A.甲队员射击成绩的中位数为7环 B.乙队员射击成绩的众数为8环
C.甲队员射击成绩的平均数为7环 D.乙队员射击成绩的平均数为7.5环
9.下面的统计图是随机抽查了某个地区的20个家庭的收入情况绘制而成,下列说法正确的是( )
这20个家庭的年平均收入为2.15万元
B.这组数据的中位数是1.15万元
C.这组数据的众数是1.3万元
D.这组数据的众数是5个
10.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是()
A.2.25 B.2.5 C.2.95 D.3
11.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
12.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )
A.50,50 B.50,30 C.80,50 D.30,50
二、填空题
1. 七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是______.
2. 在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款_________元
3. 春节期间,重庆某著名旅游景点成为热门景点,大量游客慕名前往,市旅游局统计了春节期间5天的游客数量,绘制了如图所示的折线统计图,则这五天游客数量的中位数为__.
4.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图所示的是不同捐款的人数比例,那么这个班的学生平均每人捐款_________元,中位数是_________元,众数是_________元.
5.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是___,众数是___,中位数是___.
6.在某次公益活动中,小明对本班同学的捐款情况进行统计,绘制成了如图所示的不完整的统计图,其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是_________.
7.射击比赛中,某队员10次射击成绩如图所示,则他的平均成绩是____________环.
8.如图是我国年国内生产总值增长速度统计图,则这5年增长速度的众数是_____.
三、解答题
1.如图所示的是某城市三月份1至10日最低气温的变化图象.这10天最低气温的众数是多少?中位数是多少?平均数是多少?
2.下图是某俱乐部篮球队队员年龄结构直方图,根据图中信息解答下列
问题:
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
3.小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图.
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
4.市某实验中学举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分.
方案1:所有评委所给分的平均数.
方案2:在所有评委所给分中去掉一个最高分和一个最低分,然后再计算其余评委所给分的平均数.
方案3:所有评委所给分的中位数.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计试验,如图所示的是这个同学的得分统计图.
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
5.2021年,全世界自然灾害形势严峻,洪水、地震等不仅给人们的财产带来巨大损失,更是威胁着人们的生命安全.保护生态环境即是保护民生,功在当代,利在千秋;做好综合环境治理,协调人与自然的关系,以求人和自然和谐相处迫在眉急.近日,某校组织了一场关于防自然灾害的知识讲座,并在讲座后进行了满分为100分的“防自然灾害知识测评”,为了了解学生的测评情况,该校在七、八年级中分别抽取了50名学生的分数进行整理分析,已知分数x均为整数,且分为A,B,C,D,E五个等级,分别是A:;:;:;:;:.并给出了部分信息:
【一】八年级D等级的学生人数占八年级抽取人数的20% ;
七年级C等级中最低的10个分数分别为:70,70,72,73,73,73,74,74,75,75;
【二】两个年级学生防自然灾害知识测评分数统计图:
【三】两个年级学生防自然灾害知识测评分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
七年级 76 a 72
八年级 76 75 73
(1)填空:a = ,m = ,补全条形统计图;
(2)根据以上数据,你认为在此次测评中,哪一个年级的学生对防自然灾害知识掌握较好?请说明理由(说明一条即可).
(3)若分数不低于90分表示该生对防自然灾害知识测评等级为优秀,且该校七年级有1000人,八年级有1200人,请估计该校七、八年级所有学生中,对防自然灾害知识测评等级为优秀的学生共有多少人?
6.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图.
(1)在这20位同学中,本学期购买课外书的花费的众数是多少?
(2)用两种方法计算这20位同学计划购买课外书的平均花费是多少?
7.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
8.某校八(1)班有40名学生,他们2021年纸质书阅读情况如图所示.
(1)求这40名学生纸质书阅读量的平均数、中位数和众数.
(2)班级拟进行“个人阅读达标奖”评比,为了提高学生的阅读积极性且使超过50%的同学能达标.如果你是决策者,从平均数、中位数和众数的角度进行分析,你将如何确定这个“达标标准”?
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.C.D.D.C.C.D.C.C.C.A.
二、填空题
1.3球.
2.16.
3.23.4.
4. 16 , 5 , 5 .
5.6.8,6.5,6.5.
6.20.
7.9
8.6.9%.
三、解答题
1.解:从图中可以看出,这10天的最低气温分别是℃,℃,0℃,℃,1℃,2℃,0℃,℃,2℃,2℃.其中2℃出现了3次,出现次数最多,所以这10天最低气温的众数是2℃;
把最低气温从低到高排列,第五个数据是0℃,第六个数据也是0℃,因此,该组数据的中位数是0℃;
这10个数据的平均数.所以这10天最低气温的众数是2℃,中位数和平均数都是0℃,
2.(1)平均数:=21,故平均数是21(岁);
(2)由条形统计图中出现频数最大条形最高的数据是在第三组,21岁中,故众数是21(岁);因图中是按从小到大的顺序排列的,一共十个人,中位数为第五位和第六位的平均数,第五个和第六个都是21岁,故中位数也是21(岁).
3.①这个班共有学生:5+8+12+6+8+8+3=50(名),本学期阅读量5本的有8人,
故答案为50;8;
②根据折线图可知,全班50名同学按阅读本数从小到大排列,第25名学生读了3本,第26名学生读了4本,故中位数是3.5(本),众数是3(本),
故答案为3.5;3;
③(50×40%×1+50×20%×2+50×10%×3)=1.1(本)
答:全班本学期比上学期每名同学的平均阅读量增加了1.1本.
4.解:(1)方案1的得分为(分);
方案2的得分为(分);
方案3:处于中间位置的数是8分和8分,中位数是8分,所以得分为8分;
方案4的得分为8分或8.4分.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.
5.(1)
解:根据题意,由七年级学生防自然灾害知识测评分统计图可知,
,
∴m=32,
七年级学生中,测评成绩A级有人,B级有人,C级有人,D级有人,E级有人,
测评成绩按从小到大排列,其中第25、26位为C级中74、74两个成绩,
可知七年级测评成绩中位数为,
故答案为:74,32;
八年级D等级的学生人数为:50×20%=10人,E等级的学生人数为:50﹣10﹣12﹣16﹣10=2人,
故补全条形统计图如图:
(2)
解:八年级的学生对防自然灾害知识掌握较好.理由如下:
虽然七、八年级测评成绩的平均数相同,但是八年级测评成绩的中位数和众数较高,因此八年级的测评成绩较好;
(3)
解:(人)
答:估计该校七、八年级所有学生中,对防自然灾害知识测评等级为优秀的学生共有400人.
6.(1)由扇形统计图可知,50元所占百分比最大,故众数为50元.
(2)方法一:这20位同学计划购买课外书的平均花费是:
(100×2+80×5+50×8+30×4+20×1)÷20=57(元).
方法二:这20位同学计划购买课外书的平均花费是:
100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
7.解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
8.(1)
解:平均数:,
中位数,
众数是5;
(2)
当标准为平均数6.5本,达到标准的学生有19人未超过50%;
当标准为中位数6本,达到标准的学生有26人超过50%,有利于提高学生的积极性;
当标准为众数5本,40名学生都达到标准,但不利于提高学生的积极性;
因此应该选择中位数作为标准.
一、选择题
1. 某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学均时间是( )
A. 4 B. 3 C. 2 D. 1
2. 如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A. 16,10.5 B. 8,9 C. 16,8.5 D. 8,8.5
3. 如图是我市6月份某7天的最高气温折线统计图,则这些最高气温的众数与中位数分别是()
A. 26,30°C B. 28°C,27°C
C. 28°C,28°C D. 27°C,28°C
4.某公司职工向贫困山区捐赠衣服,捐赠的衣服数量与人数之间的关系如图所示,则下列说法错误的是( )
A.参加本次捐赠的职工共有30人 B.捐赠衣服数量的众数为4件
C.捐赠衣服数量的中位数为5件 D.捐赠衣服数量的平均数为5件
5.某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
A.15.5,15.5 B.15.5,15 C.15,15.5 D.15,15
6.某汽车经销商推出A、B、C、D四种型号的小轿车进行展销,C型号轿车的成交率为50%,其它型号轿车的销售情况绘制如图,根据图中所给出信息,下列判断:
①参展四种型号的小轿车共1000辆;
②参展的D种型号小轿车有250辆;
③A型号小轿车销售的成交率最高.
其中正确的判断有( )
A.0个 B.1个 C.2个 D.3个
7.某班班长统计去年1 8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50
B.众数是42
C.中位数是58
D.每月阅读数量超过40的有4个月
8.甲、乙两名队员参加射击训练,并将他们的射击成绩分别制作成如图所示的两个统计图:
下列说法中错误的是( )
A.甲队员射击成绩的中位数为7环 B.乙队员射击成绩的众数为8环
C.甲队员射击成绩的平均数为7环 D.乙队员射击成绩的平均数为7.5环
9.下面的统计图是随机抽查了某个地区的20个家庭的收入情况绘制而成,下列说法正确的是( )
这20个家庭的年平均收入为2.15万元
B.这组数据的中位数是1.15万元
C.这组数据的众数是1.3万元
D.这组数据的众数是5个
10.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是()
A.2.25 B.2.5 C.2.95 D.3
11.小亮家1月至10月的用电量统计如图所示,这组数据的众数和中位数分别是( )
A.30和 20 B.30和25 C.30和22.5 D.30和17.5
12.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )
A.50,50 B.50,30 C.80,50 D.30,50
二、填空题
1. 七(1)班举行投篮比赛,每人投5球.如图是全班学生投进球数的扇形统计图,则投进球数的众数是______.
2. 在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图反映了不同捐款的人数比例,那么这个班的学生平均每人捐款_________元
3. 春节期间,重庆某著名旅游景点成为热门景点,大量游客慕名前往,市旅游局统计了春节期间5天的游客数量,绘制了如图所示的折线统计图,则这五天游客数量的中位数为__.
4.在一次爱心捐款中,某班有40名学生拿出自己的零花钱,有捐5元、10元、20元、50元的.如图所示的是不同捐款的人数比例,那么这个班的学生平均每人捐款_________元,中位数是_________元,众数是_________元.
5.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是___,众数是___,中位数是___.
6.在某次公益活动中,小明对本班同学的捐款情况进行统计,绘制成了如图所示的不完整的统计图,其中捐100元的人数占全班总人数的25%,则本次捐款的中位数是_________.
7.射击比赛中,某队员10次射击成绩如图所示,则他的平均成绩是____________环.
8.如图是我国年国内生产总值增长速度统计图,则这5年增长速度的众数是_____.
三、解答题
1.如图所示的是某城市三月份1至10日最低气温的变化图象.这10天最低气温的众数是多少?中位数是多少?平均数是多少?
2.下图是某俱乐部篮球队队员年龄结构直方图,根据图中信息解答下列
问题:
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
3.小明调查了全班本学期阅读课外书的情况,并根据统计数据,绘制如下的频率分布折线图和扇形统计图.
根据以上信息,回答下列问题:
①这个班共有__________ 名学生,本学期阅读量5本的有________ 人
②这个班本学期阅读量的中位数是_______ 本,众数是 ______ 本;
③求全班本学期比上学期每名同学的平均阅读量增加了多少本?
4.市某实验中学举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分.
方案1:所有评委所给分的平均数.
方案2:在所有评委所给分中去掉一个最高分和一个最低分,然后再计算其余评委所给分的平均数.
方案3:所有评委所给分的中位数.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计试验,如图所示的是这个同学的得分统计图.
(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
5.2021年,全世界自然灾害形势严峻,洪水、地震等不仅给人们的财产带来巨大损失,更是威胁着人们的生命安全.保护生态环境即是保护民生,功在当代,利在千秋;做好综合环境治理,协调人与自然的关系,以求人和自然和谐相处迫在眉急.近日,某校组织了一场关于防自然灾害的知识讲座,并在讲座后进行了满分为100分的“防自然灾害知识测评”,为了了解学生的测评情况,该校在七、八年级中分别抽取了50名学生的分数进行整理分析,已知分数x均为整数,且分为A,B,C,D,E五个等级,分别是A:;:;:;:;:.并给出了部分信息:
【一】八年级D等级的学生人数占八年级抽取人数的20% ;
七年级C等级中最低的10个分数分别为:70,70,72,73,73,73,74,74,75,75;
【二】两个年级学生防自然灾害知识测评分数统计图:
【三】两个年级学生防自然灾害知识测评分数样本数据的平均数、中位数、众数如下:
平均数 中位数 众数
七年级 76 a 72
八年级 76 75 73
(1)填空:a = ,m = ,补全条形统计图;
(2)根据以上数据,你认为在此次测评中,哪一个年级的学生对防自然灾害知识掌握较好?请说明理由(说明一条即可).
(3)若分数不低于90分表示该生对防自然灾害知识测评等级为优秀,且该校七年级有1000人,八年级有1200人,请估计该校七、八年级所有学生中,对防自然灾害知识测评等级为优秀的学生共有多少人?
6.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图.
(1)在这20位同学中,本学期购买课外书的花费的众数是多少?
(2)用两种方法计算这20位同学计划购买课外书的平均花费是多少?
7.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
8.某校八(1)班有40名学生,他们2021年纸质书阅读情况如图所示.
(1)求这40名学生纸质书阅读量的平均数、中位数和众数.
(2)班级拟进行“个人阅读达标奖”评比,为了提高学生的阅读积极性且使超过50%的同学能达标.如果你是决策者,从平均数、中位数和众数的角度进行分析,你将如何确定这个“达标标准”?
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.C.D.D.C.C.D.C.C.C.A.
二、填空题
1.3球.
2.16.
3.23.4.
4. 16 , 5 , 5 .
5.6.8,6.5,6.5.
6.20.
7.9
8.6.9%.
三、解答题
1.解:从图中可以看出,这10天的最低气温分别是℃,℃,0℃,℃,1℃,2℃,0℃,℃,2℃,2℃.其中2℃出现了3次,出现次数最多,所以这10天最低气温的众数是2℃;
把最低气温从低到高排列,第五个数据是0℃,第六个数据也是0℃,因此,该组数据的中位数是0℃;
这10个数据的平均数.所以这10天最低气温的众数是2℃,中位数和平均数都是0℃,
2.(1)平均数:=21,故平均数是21(岁);
(2)由条形统计图中出现频数最大条形最高的数据是在第三组,21岁中,故众数是21(岁);因图中是按从小到大的顺序排列的,一共十个人,中位数为第五位和第六位的平均数,第五个和第六个都是21岁,故中位数也是21(岁).
3.①这个班共有学生:5+8+12+6+8+8+3=50(名),本学期阅读量5本的有8人,
故答案为50;8;
②根据折线图可知,全班50名同学按阅读本数从小到大排列,第25名学生读了3本,第26名学生读了4本,故中位数是3.5(本),众数是3(本),
故答案为3.5;3;
③(50×40%×1+50×20%×2+50×10%×3)=1.1(本)
答:全班本学期比上学期每名同学的平均阅读量增加了1.1本.
4.解:(1)方案1的得分为(分);
方案2的得分为(分);
方案3:处于中间位置的数是8分和8分,中位数是8分,所以得分为8分;
方案4的得分为8分或8.4分.
(2)因为方案1中的平均数受极端数值的影响,不适合作为这个同学演讲的最后得分,
所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.
5.(1)
解:根据题意,由七年级学生防自然灾害知识测评分统计图可知,
,
∴m=32,
七年级学生中,测评成绩A级有人,B级有人,C级有人,D级有人,E级有人,
测评成绩按从小到大排列,其中第25、26位为C级中74、74两个成绩,
可知七年级测评成绩中位数为,
故答案为:74,32;
八年级D等级的学生人数为:50×20%=10人,E等级的学生人数为:50﹣10﹣12﹣16﹣10=2人,
故补全条形统计图如图:
(2)
解:八年级的学生对防自然灾害知识掌握较好.理由如下:
虽然七、八年级测评成绩的平均数相同,但是八年级测评成绩的中位数和众数较高,因此八年级的测评成绩较好;
(3)
解:(人)
答:估计该校七、八年级所有学生中,对防自然灾害知识测评等级为优秀的学生共有400人.
6.(1)由扇形统计图可知,50元所占百分比最大,故众数为50元.
(2)方法一:这20位同学计划购买课外书的平均花费是:
(100×2+80×5+50×8+30×4+20×1)÷20=57(元).
方法二:这20位同学计划购买课外书的平均花费是:
100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
7.解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
8.(1)
解:平均数:,
中位数,
众数是5;
(2)
当标准为平均数6.5本,达到标准的学生有19人未超过50%;
当标准为中位数6本,达到标准的学生有26人超过50%,有利于提高学生的积极性;
当标准为众数5本,40名学生都达到标准,但不利于提高学生的积极性;
因此应该选择中位数作为标准.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
