北师大版八年级数学上册试题 7.4平行线的性质(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 7.4平行线的性质(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 510.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 13:07:09 | ||
图片预览




文档简介
7.4平行线的性质
一、选择题
1.如图,已知AB∥CD,FG平分∠EFD交AB于点G,若∠AEF=70°,则∠EFG的度数为( )
A.30° B.35° C.40° D.45°
2.如图,直线,将一个含角的三角尺按如图所示的位置放置,若,则的度数为( )
A. B. C. D.
3.如图,平分,BE⊥AC,,图中与∠C互余的角有( )
A.1个 B.2个
C.3个 D.4个
4.在钝角△ABC中,延长BA到D,AE是∠DAC的平分线,AE//BC,则与∠B相等的角有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在中,,,,则( )
A. B. C. D.
6.如图,平行线被直线所截,交点为,且,若,则的度数为( )
A.30° B.40° C.50° D.60°
7.如图,直线m∥n,被直线a所截,若∠1=3∠2.则∠1的大小为( )
A.120° B.150° C.140° D.135°
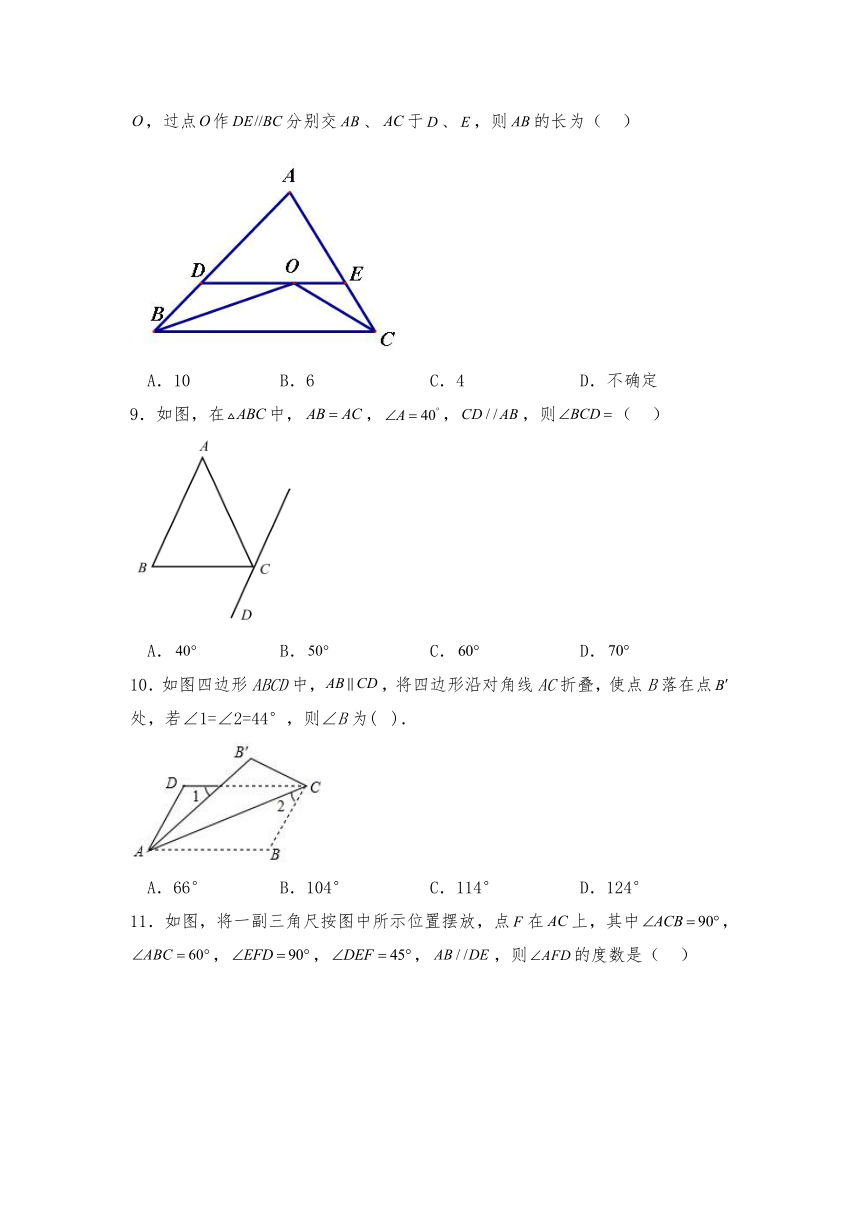
8.如图,在中,,的周长10,和的平分线交于点,过点作分别交、于、,则的长为( )
A.10 B.6 C.4 D.不确定
9.如图,在中,,,,则( )
A. B. C. D.
10.如图四边形ABCD中,,将四边形沿对角线AC折叠,使点B落在点处,若∠1=∠2=44°,则∠B为( ).
A.66° B.104° C.114° D.124°
11.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
二、填空题
1.将△ABC沿着DE翻折,使点A落到点A′处,A′D、A′E分别与BC交于M、N两点,且DEBC.已知∠A′NM=27°,则∠NEC=_____.
2.如图,AB∥CD,若∠1=60°,则∠2=_____°.
3.将直尺和直角三角板按如图所示方式摆放,已知,则的大小是_____________.
4.如图,,且CF平分∠AFE,若,则∠A的度数是__.
5.在五边形中,,,,则的度数是______.
6.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=∠EFD=90°,∠ABC=60°,∠DEF=45°,AB∥DE,则∠AFD的大小为___________度.
7.如图所示,的两条角平分线相交于点,过点作EFBC,交于点,交于点,若的周长为,则______cm.
8.如图,一块余料,,现进行如下操作:以点为圆心,适当长为半径作圆弧,分别交,于点,;再分别以点,为圆心,大于的长为半径作圆弧,两弧在内部相交于点,画射线,交于点.连结、.若,则的度数为_____度.
9.如图,已知//,,,则______度.
10.如图,ABCD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是_____.
三、解答题
1.如图,B是线段AC的中点,,求证:.
2.如图,中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且.
(1)求证:≌;
(2)若,,试求DE的长.
3.如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
4.如图,, .
(1)试说明;
(2)若,且,求的度数.
5.如图,AB,CD相交于点O,AC∥DB,OA=OB,E、F分别是OC,OD中点.
(1)求证:OD=OC.
(2) 求证:四边形AFBE平行四边形.
6.完成下面的证明如图.
已知:AD∥EF,∠1=∠2,求证:AD平分∠BAC.
证明:∵AD∥EF ( ),
∴∠2= ( ),
∠1= ( ).
∵∠1=∠2(已知),
∴∠BAD=∠CAD( ).
即AD平分∠BAC.
7.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.C.C.C.D.C.D.B.D.C.A.
二、填空题
1.126°.
2.60.
3.35°
4..
5..
6.15.
7..
8.28.
9.60°
10.5.
三、解答题
1.证明∵B是AC中点,
∴AB=BC,
∵,
∴∠A=∠EBC,
∵,
∴∠DBA=∠C,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(ASA).
2.(1)
证明:∵BE∥CF,∴∠BED=∠CFD,
∵∠BDE=∠CDF,BD=CD,
∴△BDE≌△CDF(AAS);
(2)
解:由(1)结论可得DE=DF,
∵EF=AE-AF=15-8=7,
∴DE=;
3.证明:∵AB∥DE,
∴∠B=∠D,
∵EC⊥BD,∠A=90°,
∴∠DCE=90°=∠A,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA),
∴AC=CE.
4.(1)解:∵,∴BM∥CN,∴∠CBM=∠BCN,∵,∴∠3+∠CBM=∠4+∠BCN,即∠ABC=∠BCD,∴AB∥CD;
(2)解:∵∠ABD=∠EBF,,∴∠ABD=110°,∴∠BAD+∠BDA=70°,∵,∴∠BAD=35°,∵AB∥CD,∴∠ADC=∠BAD=35°.
5.证明:(1)∵AC∥DB,
∴∠CAO=∠DBO,
∵∠AOC=∠BOD,OA=OB,
∴△AOC≌△BOD,
∴OC=OD;
(2)∵E是OC中点,F是OD中点,
∴OE=OC,OF=OD,
∵OC=OD,
∴OE=OF,
又∵OA=OB,
∴四边形AFBE是平行四边形.
6.解:∵AD∥EF(已知),
∴∠2=∠CAD(两直线平行,同位角相等),
∠1=∠BAD(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠CAD=∠BAD(等量代换),
即AD平分∠BAC(角平分线的定义).
7.∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
一、选择题
1.如图,已知AB∥CD,FG平分∠EFD交AB于点G,若∠AEF=70°,则∠EFG的度数为( )
A.30° B.35° C.40° D.45°
2.如图,直线,将一个含角的三角尺按如图所示的位置放置,若,则的度数为( )
A. B. C. D.
3.如图,平分,BE⊥AC,,图中与∠C互余的角有( )
A.1个 B.2个
C.3个 D.4个
4.在钝角△ABC中,延长BA到D,AE是∠DAC的平分线,AE//BC,则与∠B相等的角有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在中,,,,则( )
A. B. C. D.
6.如图,平行线被直线所截,交点为,且,若,则的度数为( )
A.30° B.40° C.50° D.60°
7.如图,直线m∥n,被直线a所截,若∠1=3∠2.则∠1的大小为( )
A.120° B.150° C.140° D.135°
8.如图,在中,,的周长10,和的平分线交于点,过点作分别交、于、,则的长为( )
A.10 B.6 C.4 D.不确定
9.如图,在中,,,,则( )
A. B. C. D.
10.如图四边形ABCD中,,将四边形沿对角线AC折叠,使点B落在点处,若∠1=∠2=44°,则∠B为( ).
A.66° B.104° C.114° D.124°
11.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
二、填空题
1.将△ABC沿着DE翻折,使点A落到点A′处,A′D、A′E分别与BC交于M、N两点,且DEBC.已知∠A′NM=27°,则∠NEC=_____.
2.如图,AB∥CD,若∠1=60°,则∠2=_____°.
3.将直尺和直角三角板按如图所示方式摆放,已知,则的大小是_____________.
4.如图,,且CF平分∠AFE,若,则∠A的度数是__.
5.在五边形中,,,,则的度数是______.
6.如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=∠EFD=90°,∠ABC=60°,∠DEF=45°,AB∥DE,则∠AFD的大小为___________度.
7.如图所示,的两条角平分线相交于点,过点作EFBC,交于点,交于点,若的周长为,则______cm.
8.如图,一块余料,,现进行如下操作:以点为圆心,适当长为半径作圆弧,分别交,于点,;再分别以点,为圆心,大于的长为半径作圆弧,两弧在内部相交于点,画射线,交于点.连结、.若,则的度数为_____度.
9.如图,已知//,,,则______度.
10.如图,ABCD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是_____.
三、解答题
1.如图,B是线段AC的中点,,求证:.
2.如图,中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且.
(1)求证:≌;
(2)若,,试求DE的长.
3.如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
4.如图,, .
(1)试说明;
(2)若,且,求的度数.
5.如图,AB,CD相交于点O,AC∥DB,OA=OB,E、F分别是OC,OD中点.
(1)求证:OD=OC.
(2) 求证:四边形AFBE平行四边形.
6.完成下面的证明如图.
已知:AD∥EF,∠1=∠2,求证:AD平分∠BAC.
证明:∵AD∥EF ( ),
∴∠2= ( ),
∠1= ( ).
∵∠1=∠2(已知),
∴∠BAD=∠CAD( ).
即AD平分∠BAC.
7.如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.C.C.C.D.C.D.B.D.C.A.
二、填空题
1.126°.
2.60.
3.35°
4..
5..
6.15.
7..
8.28.
9.60°
10.5.
三、解答题
1.证明∵B是AC中点,
∴AB=BC,
∵,
∴∠A=∠EBC,
∵,
∴∠DBA=∠C,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(ASA).
2.(1)
证明:∵BE∥CF,∴∠BED=∠CFD,
∵∠BDE=∠CDF,BD=CD,
∴△BDE≌△CDF(AAS);
(2)
解:由(1)结论可得DE=DF,
∵EF=AE-AF=15-8=7,
∴DE=;
3.证明:∵AB∥DE,
∴∠B=∠D,
∵EC⊥BD,∠A=90°,
∴∠DCE=90°=∠A,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA),
∴AC=CE.
4.(1)解:∵,∴BM∥CN,∴∠CBM=∠BCN,∵,∴∠3+∠CBM=∠4+∠BCN,即∠ABC=∠BCD,∴AB∥CD;
(2)解:∵∠ABD=∠EBF,,∴∠ABD=110°,∴∠BAD+∠BDA=70°,∵,∴∠BAD=35°,∵AB∥CD,∴∠ADC=∠BAD=35°.
5.证明:(1)∵AC∥DB,
∴∠CAO=∠DBO,
∵∠AOC=∠BOD,OA=OB,
∴△AOC≌△BOD,
∴OC=OD;
(2)∵E是OC中点,F是OD中点,
∴OE=OC,OF=OD,
∵OC=OD,
∴OE=OF,
又∵OA=OB,
∴四边形AFBE是平行四边形.
6.解:∵AD∥EF(已知),
∴∠2=∠CAD(两直线平行,同位角相等),
∠1=∠BAD(两直线平行,内错角相等),
∵∠1=∠2(已知),
∴∠CAD=∠BAD(等量代换),
即AD平分∠BAC(角平分线的定义).
7.∵EF∥GH,∴∠ABD+∠FAC=180°,∴∠ABD=180°﹣72°=108°,∵∠ABD=∠ACD+∠BDC,∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
