3. 切线(一[上学期]
图片预览







文档简介
课件21张PPT。 3. 切 线(一)一、情境引入 1、 下雨天,当你转动雨伞,你会发现雨伞上的水珠顺着伞面的边缘
飞出.仔细观察一下,水珠是顺着什么样的方向飞出的?
2、用机床打磨铁制零件时,铁屑是沿什么方向飞出的?
3、行驶中的火车,火车的车轮与笔直的铁轨给我们什么形象?
二、复习回顾 1.切线的识别方法:
(1)利用切线的定义,与圆只有 一个公共点的直线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
三、实践活动, 探究新知 【活动内容】
探究切线的其它识别方法
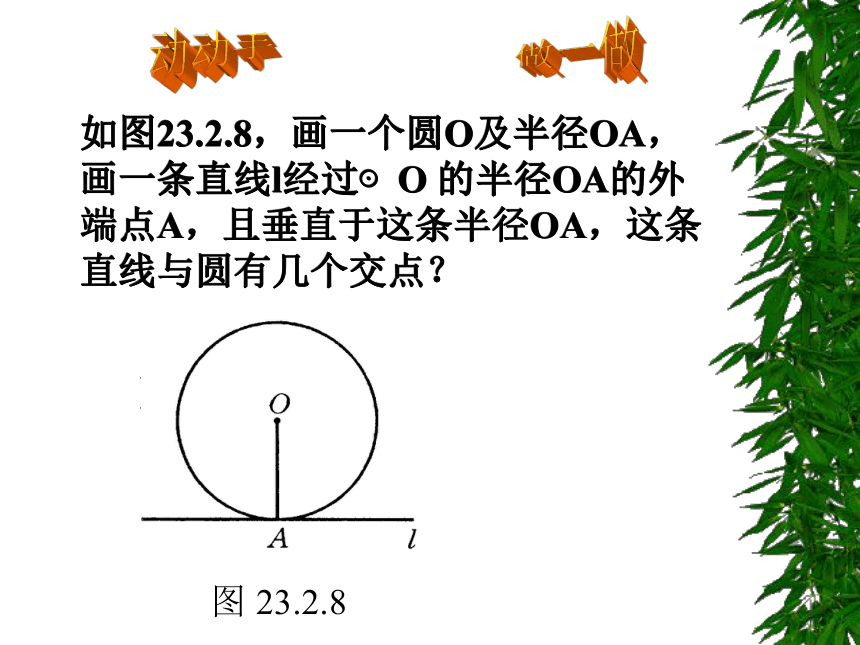
如图23.2.8,画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
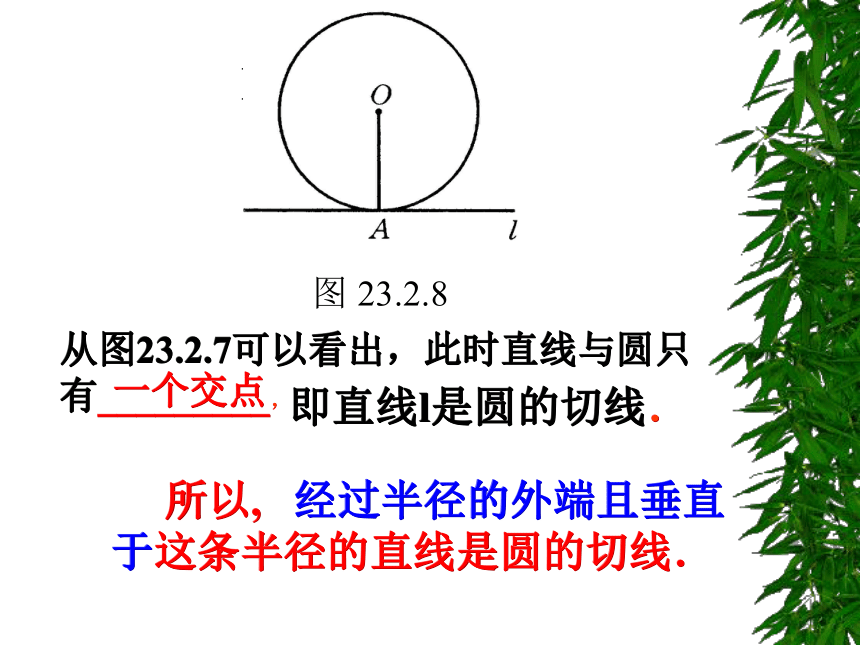
动动手做一做从图23.2.7可以看出,此时直线与圆只有_________, 即直线l是圆的切线. 所以, 经过半径的外端且垂直于这条半径的直线是圆的切线.一个交点 【重点1】切线的识别方法 (1)利用切线的定义,与圆只有 一个公共点的直线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线.
(三种)课堂练习 1 1.????? 是非题:
(1)垂直于圆的半径的直线一定是这个圆的切线. ( )
(2)过圆的半径的外端的直线一定是这个圆的切线. ( )××思 考1 如图23.2.8,如果直线l是⊙O的切线,点A为切点,那么半径OA与l一定垂直吗?
【解】一定垂直.由于l是⊙O的切线,圆心O到直线l的距离等于半径,所以OA是圆心O到直线l的距离,因此l⊥OA,这就是说,圆的切线一定垂直于经过切点的半径.
圆的切线一定垂直于经过切点的半径吗?
思 考2经过圆心且垂直于切线的直线必经过切点吗?
结论:必经过即:经过圆心且垂直于切线的直线必经过切点.
思 考3经过切点且垂直于切线的直线必经过圆心吗?
答:必经过即:经过切点且垂直于切线的直线必经过圆心.
【重点2】切线的性质 (1)圆的切线一定垂直于经过切点的半径.
(2)经过圆心且垂直于切线的直线必经过切点.
(3)经过切点且垂直于切线的直线必经过圆心.
(三条) 【附注】切线的三条性质可总结如下: 如果一条直线符合下列条件中的任意两个,那么它一定满足第三个条件. 这三个条件是: a.直线过圆心; b.直线过切点; c.直线与圆的切线垂直. 四、例题 例. 如图23.2.9,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解 直线AB是⊙O的切线.
因为AB=OA,且∠OBA=45°,所以∠AOB=45°,∠OAB=90°.根据经过半径的外端且垂直于这条半径的直线是圆的切线,可知直线AB是⊙O的切线.
课堂练习 2 .?2.?? 如图,AB是⊙O的直径,∠B=45°,AC=AB.AC是⊙O的切线吗?为什么?
课堂练习 2 .解:是.因为由∠B=45°,AC=AB,根据等腰三角形的性质,得出∠BAC=90 °,而OA是⊙O的半径,根据“经过半径的外端且垂直于这条半径的直线是圆的切线”,因此, AC是⊙O的切线3. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D. BD是⊙O的切线吗?为什么?.解:是.由∠BAD=30°, 得出∠BOD=60 °.因为在⊿ODB中,由∠B=30°,
∠BOD=60 °, 得∠BOD=90°,所以, BD是⊙O的切线4. 以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形.直角 五、课堂小结 1.切线的识别方法(三种):
(1)利用切线的定义,与圆只有 一个公共点的直 线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线. 2.切线的性质(三条):
(1) 圆的切线垂直于经过切点的半径.(2)经过圆心且垂直于切线的直线必经过切点.
(3)经过切点且垂直于切线的直线必经过圆心六、布置作业 下发试卷 再见!
飞出.仔细观察一下,水珠是顺着什么样的方向飞出的?
2、用机床打磨铁制零件时,铁屑是沿什么方向飞出的?
3、行驶中的火车,火车的车轮与笔直的铁轨给我们什么形象?
二、复习回顾 1.切线的识别方法:
(1)利用切线的定义,与圆只有 一个公共点的直线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
三、实践活动, 探究新知 【活动内容】
探究切线的其它识别方法
如图23.2.8,画一个圆O及半径OA,画一条直线l经过⊙O 的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
动动手做一做从图23.2.7可以看出,此时直线与圆只有_________, 即直线l是圆的切线. 所以, 经过半径的外端且垂直于这条半径的直线是圆的切线.一个交点 【重点1】切线的识别方法 (1)利用切线的定义,与圆只有 一个公共点的直线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线.
(三种)课堂练习 1 1.????? 是非题:
(1)垂直于圆的半径的直线一定是这个圆的切线. ( )
(2)过圆的半径的外端的直线一定是这个圆的切线. ( )××思 考1 如图23.2.8,如果直线l是⊙O的切线,点A为切点,那么半径OA与l一定垂直吗?
【解】一定垂直.由于l是⊙O的切线,圆心O到直线l的距离等于半径,所以OA是圆心O到直线l的距离,因此l⊥OA,这就是说,圆的切线一定垂直于经过切点的半径.
圆的切线一定垂直于经过切点的半径吗?
思 考2经过圆心且垂直于切线的直线必经过切点吗?
结论:必经过即:经过圆心且垂直于切线的直线必经过切点.
思 考3经过切点且垂直于切线的直线必经过圆心吗?
答:必经过即:经过切点且垂直于切线的直线必经过圆心.
【重点2】切线的性质 (1)圆的切线一定垂直于经过切点的半径.
(2)经过圆心且垂直于切线的直线必经过切点.
(3)经过切点且垂直于切线的直线必经过圆心.
(三条) 【附注】切线的三条性质可总结如下: 如果一条直线符合下列条件中的任意两个,那么它一定满足第三个条件. 这三个条件是: a.直线过圆心; b.直线过切点; c.直线与圆的切线垂直. 四、例题 例. 如图23.2.9,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解 直线AB是⊙O的切线.
因为AB=OA,且∠OBA=45°,所以∠AOB=45°,∠OAB=90°.根据经过半径的外端且垂直于这条半径的直线是圆的切线,可知直线AB是⊙O的切线.
课堂练习 2 .?2.?? 如图,AB是⊙O的直径,∠B=45°,AC=AB.AC是⊙O的切线吗?为什么?
课堂练习 2 .解:是.因为由∠B=45°,AC=AB,根据等腰三角形的性质,得出∠BAC=90 °,而OA是⊙O的半径,根据“经过半径的外端且垂直于这条半径的直线是圆的切线”,因此, AC是⊙O的切线3. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D. BD是⊙O的切线吗?为什么?.解:是.由∠BAD=30°, 得出∠BOD=60 °.因为在⊿ODB中,由∠B=30°,
∠BOD=60 °, 得∠BOD=90°,所以, BD是⊙O的切线4. 以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形.直角 五、课堂小结 1.切线的识别方法(三种):
(1)利用切线的定义,与圆只有 一个公共点的直 线, 是圆的切线;
(2)圆心到直线的距离等于半径的直线,是圆的切线;
* (3) 经过半径的外端且垂直于这条半径的直线是圆的切线. 2.切线的性质(三条):
(1) 圆的切线垂直于经过切点的半径.(2)经过圆心且垂直于切线的直线必经过切点.
(3)经过切点且垂直于切线的直线必经过圆心六、布置作业 下发试卷 再见!
