3. 切线(二)[上学期]
图片预览



文档简介
课件13张PPT。 3. 切 线(二)一、复习回顾 1.过⊙O上一点P作⊙O的切线,你能作出几条?
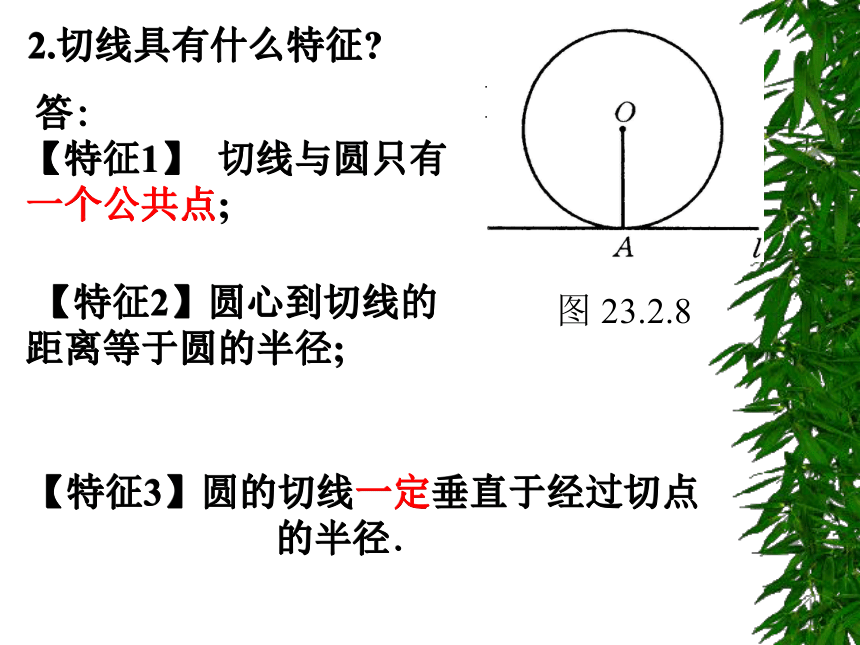
2.切线具有什么特征?
答:
【特征1】 切线与圆只有 一个公共点;
【特征2】圆心到切线的距离等于圆的半径;
【特征3】圆的切线一定垂直于经过切点的半径.
二、进入新课 试一试:过⊙O外一点P作⊙O的切线,你能作出几条?
【重点1】切线长及性质 1. 【切线长概念】我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长,如图23.2.10,线段PA、PB的长就是点P到⊙O的切线长.
2. 【切线长性质】从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角. 如图:PA、PB是⊙O的两条切线,则
(1)PA=PB;
(2)∠APO= ∠BPO.
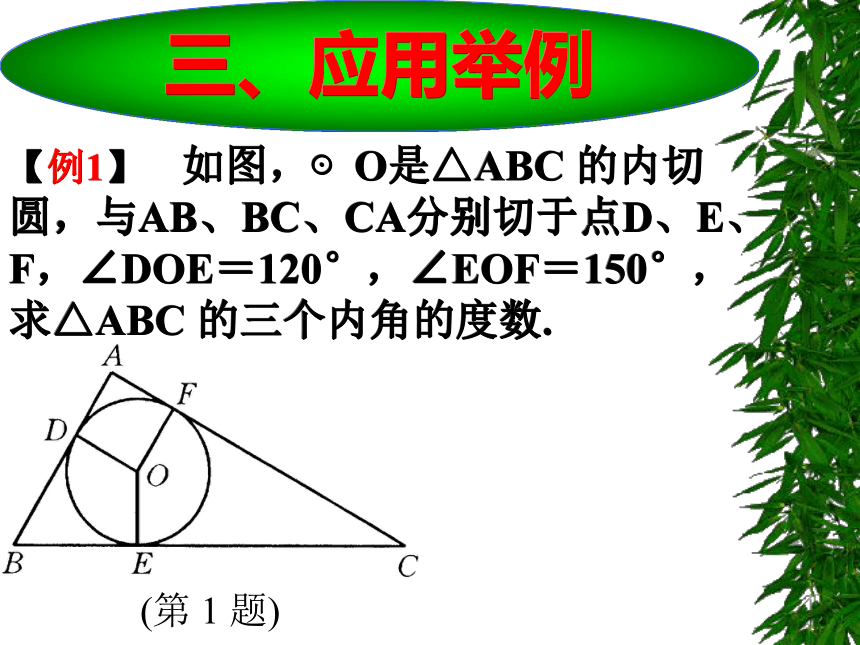
三、应用举例 【例1】 如图,⊙O是△ABC 的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC 的三个内角的度数.
∵ ∠DOE=120° , ∠EOF=150°
∴ ∠DOF= 360°- ∠DOE -∠EOF
=360°- 120°- 150°=90° 【解】∵ AB、AC分别切⊙O于点D、F
∴ ∠ADO= ∠AFO=90°
∴ ∠A=360°- ∠ADO - ∠DOF- ∠AFO
=360° -90° -90° -90°=90°
同理 ∠B=60°, ∠C=30°.【例2】 △ABC 的内切圆⊙O 与AB、BC 、 AC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,求AD、BE和CF的长.
解:设AD=x, BE=y, CF=z, 由切线长性质可知:
AD=AF,BD=BE,CE=CF
即AD=1厘米,BE =4厘米,CF =5厘米
四、探索 如图23.2.11为一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮?
【重点2】三角形的内切圆 与三角形各边都相切的圆叫做三角形的内切圆.三角形的内切圆的圆心叫做三角形的内心.这个三角形叫做圆的外切三角形.三角形的内心就是三角形三条内角平分线的交点.一个三角形的内切圆是惟一的. 【例3】设△ABC 的内切圆的半径为r,△ABC 的周长为l,求△ABC 的面积S.
五、课堂小结 1.【切线长概念】圆的切线上某一点与切点之间的线段长叫做这点到圆的切线长.
2. 【切线长性质】从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角. 3. 【三角形的内切圆】:与三角形三边都相切的圆叫三角形的内切圆,该圆的圆心叫做三角形的内心:即三角形三条内角平分线的交点. 六、布置作业 课本P60 【 练习】1,2,3题 (注:要抄题,要画图。) 再见谢谢大家
2.切线具有什么特征?
答:
【特征1】 切线与圆只有 一个公共点;
【特征2】圆心到切线的距离等于圆的半径;
【特征3】圆的切线一定垂直于经过切点的半径.
二、进入新课 试一试:过⊙O外一点P作⊙O的切线,你能作出几条?
【重点1】切线长及性质 1. 【切线长概念】我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长,如图23.2.10,线段PA、PB的长就是点P到⊙O的切线长.
2. 【切线长性质】从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角. 如图:PA、PB是⊙O的两条切线,则
(1)PA=PB;
(2)∠APO= ∠BPO.
三、应用举例 【例1】 如图,⊙O是△ABC 的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC 的三个内角的度数.
∵ ∠DOE=120° , ∠EOF=150°
∴ ∠DOF= 360°- ∠DOE -∠EOF
=360°- 120°- 150°=90° 【解】∵ AB、AC分别切⊙O于点D、F
∴ ∠ADO= ∠AFO=90°
∴ ∠A=360°- ∠ADO - ∠DOF- ∠AFO
=360° -90° -90° -90°=90°
同理 ∠B=60°, ∠C=30°.【例2】 △ABC 的内切圆⊙O 与AB、BC 、 AC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,求AD、BE和CF的长.
解:设AD=x, BE=y, CF=z, 由切线长性质可知:
AD=AF,BD=BE,CE=CF
即AD=1厘米,BE =4厘米,CF =5厘米
四、探索 如图23.2.11为一张三角形铁皮,如何在它上面截一个面积最大的圆形铁皮?
【重点2】三角形的内切圆 与三角形各边都相切的圆叫做三角形的内切圆.三角形的内切圆的圆心叫做三角形的内心.这个三角形叫做圆的外切三角形.三角形的内心就是三角形三条内角平分线的交点.一个三角形的内切圆是惟一的. 【例3】设△ABC 的内切圆的半径为r,△ABC 的周长为l,求△ABC 的面积S.
五、课堂小结 1.【切线长概念】圆的切线上某一点与切点之间的线段长叫做这点到圆的切线长.
2. 【切线长性质】从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角. 3. 【三角形的内切圆】:与三角形三边都相切的圆叫三角形的内切圆,该圆的圆心叫做三角形的内心:即三角形三条内角平分线的交点. 六、布置作业 课本P60 【 练习】1,2,3题 (注:要抄题,要画图。) 再见谢谢大家
