13.3.1等腰三角形(第2课时)判定——课件
文档属性
| 名称 | 13.3.1等腰三角形(第2课时)判定——课件 |  | |
| 格式 | zip | ||
| 文件大小 | 28.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-14 11:35:43 | ||
图片预览




文档简介
课件12张PPT。13.3.1 等腰三角形的判定1.理解并识记等腰三角形的判定方法,并会运用。
2.会等腰三角形的性质和判定的综合运用。学习目标:认真看课本P77练习下面——P78。
注意:
1.解答P77“思考”中的问题。
2.把例2补充完整,思考如何对一个命题进行证明。
3.例3中已知底边和底边上的高作等腰三角形的方法。
6分钟后,比谁能正确运用等腰三角形的判定做对检测题。
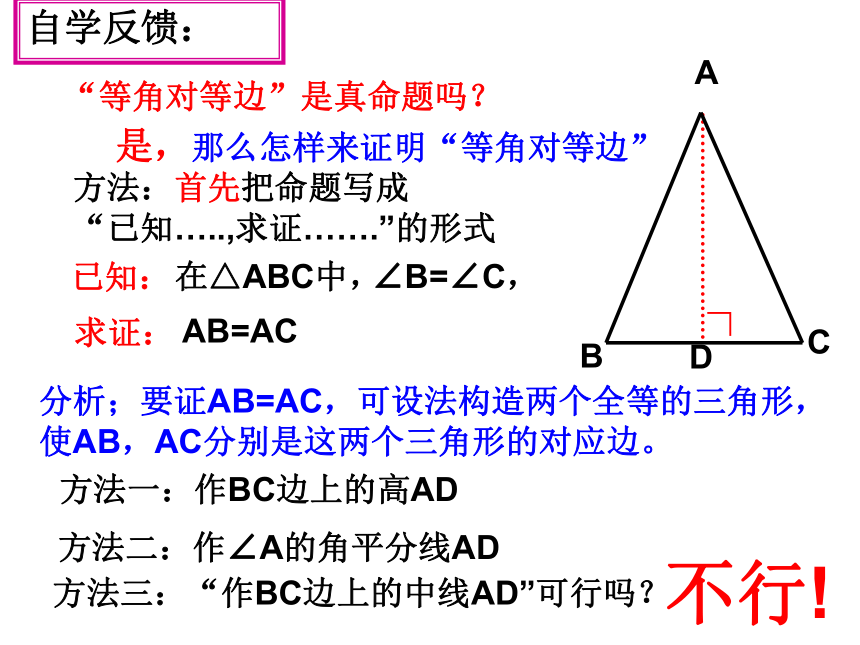
自学指导:“等角对等边”是真命题吗?已知:ABCD是,那么怎样来证明“等角对等边”方法:首先把命题写成
“已知…..,求证…….”的形式方法一:作BC边上的高AD方法二:作∠A的角平分线AD方法三:“作BC边上的中线AD”可行吗?在△ABC中,
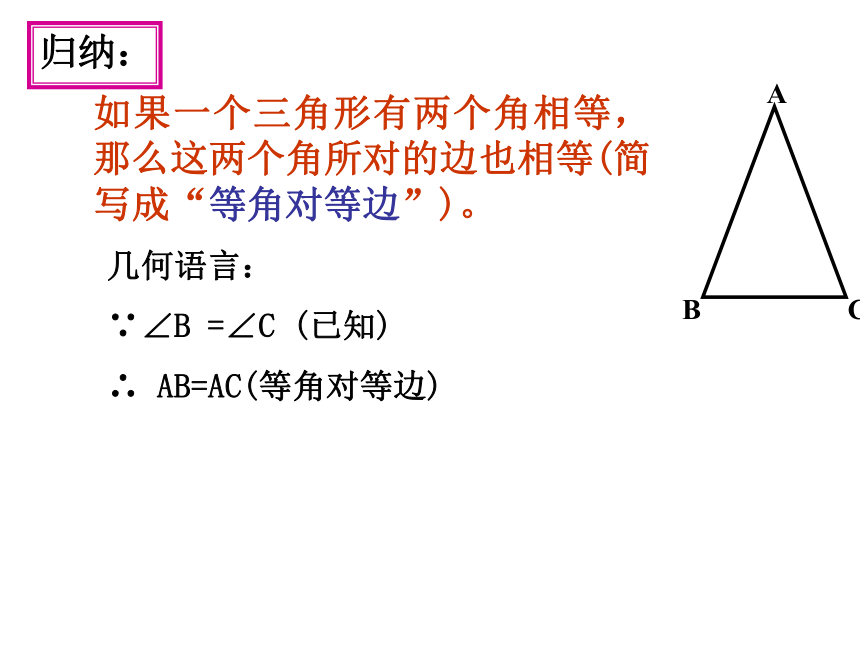
∠B=∠C,求证:AB=AC分析;要证AB=AC,可设法构造两个全等的三角形,使AB,AC分别是这两个三角形的对应边。∟不行!自学反馈:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。几何语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边) 归纳:例题2拓展一
已知:∠EAC是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC 证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵AB=AC,
∴∠B=∠C.
∴∠EAD=∠DAC.
即 AD平分∠EAC...自学反馈:证明:∵AD平分∠EAC,
∴∠EAC=2∠DAC.
∵AB=AC,
∴∠B=∠C.
又∵∠EAC是△ABC的外角,
∴∠EAC=∠B+∠C=2∠C.
∴∠DAC=∠C.
∴AD∥BC. 例题2拓展二
已知:∠EAC是△ABC的外角,
求证: AD平分∠EAC,且 AB=AC.AD∥BC.自学反馈:P79:练习1、2、4检测题:你有哪些方法可以判定一个三角形是等腰三角形?利用定义证明“中垂线性质”“等角对等边”课堂小结:有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等 运用等腰三角形的判定定理时,应注意在同一个三角形中.课堂小结:必做题:P82: 2、5
选做题:P79: 3
思考题:P82: 6当堂检测:2、已知:如图,AD ∥BC,BD平分∠ABC。求证:AB=AD证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵ BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD1、已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。等腰直角三角形有: △ABC ,△ACD ,△BCD。补充习题:
2.会等腰三角形的性质和判定的综合运用。学习目标:认真看课本P77练习下面——P78。
注意:
1.解答P77“思考”中的问题。
2.把例2补充完整,思考如何对一个命题进行证明。
3.例3中已知底边和底边上的高作等腰三角形的方法。
6分钟后,比谁能正确运用等腰三角形的判定做对检测题。
自学指导:“等角对等边”是真命题吗?已知:ABCD是,那么怎样来证明“等角对等边”方法:首先把命题写成
“已知…..,求证…….”的形式方法一:作BC边上的高AD方法二:作∠A的角平分线AD方法三:“作BC边上的中线AD”可行吗?在△ABC中,
∠B=∠C,求证:AB=AC分析;要证AB=AC,可设法构造两个全等的三角形,使AB,AC分别是这两个三角形的对应边。∟不行!自学反馈:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。几何语言:
∵∠B =∠C (已知)
∴ AB=AC(等角对等边) 归纳:例题2拓展一
已知:∠EAC是△ABC的外角,
,且 AD∥BC.
求证: AD平分∠EAC AB=AC 证明:∵AD∥BC,
∴∠EAD=∠B,
∠DAC=∠C.
∵AB=AC,
∴∠B=∠C.
∴∠EAD=∠DAC.
即 AD平分∠EAC...自学反馈:证明:∵AD平分∠EAC,
∴∠EAC=2∠DAC.
∵AB=AC,
∴∠B=∠C.
又∵∠EAC是△ABC的外角,
∴∠EAC=∠B+∠C=2∠C.
∴∠DAC=∠C.
∴AD∥BC. 例题2拓展二
已知:∠EAC是△ABC的外角,
求证: AD平分∠EAC,且 AB=AC.AD∥BC.自学反馈:P79:练习1、2、4检测题:你有哪些方法可以判定一个三角形是等腰三角形?利用定义证明“中垂线性质”“等角对等边”课堂小结:有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等 运用等腰三角形的判定定理时,应注意在同一个三角形中.课堂小结:必做题:P82: 2、5
选做题:P79: 3
思考题:P82: 6当堂检测:2、已知:如图,AD ∥BC,BD平分∠ABC。求证:AB=AD证明:∵ AD ∥BC
∴∠ADB=∠DBC
∵ BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD1、已知:如图,CD是等腰直角三角形ABC斜边上的高,找出图中有哪些等腰直角三角形。等腰直角三角形有: △ABC ,△ACD ,△BCD。补充习题:
