平行线的识别[上学期]
图片预览






文档简介
课件16张PPT。平行线的识别一、温故知新二、我们的问题三、探索新的、有效的方法四、实践园地五、看看我们这节课学了些什么一、温故知新判断下列的正误!
1、任何两条不相交的直线,叫做平行线.
2、已知直线a,则a的平行线只有1条.
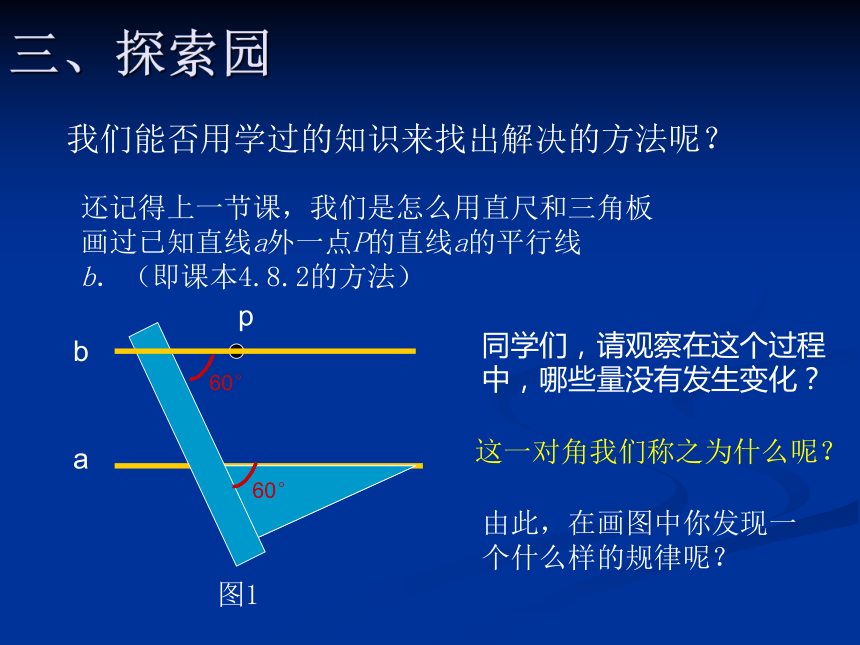
3、在同一平面内,如果直线a与直线b无交点,直线b与直线c无交点,则直线a与直线c平行. 二、我们的问题:请观察右边图中的两条直线a和直线b,它们是什么位置关系?是相交?还是平行呢,你通过什么来判断的?ab显然,我们无法通过眼睛来直接判断,因为眼睛只是一个直观上的判断,那么我们能不能找到一种可以有效识别平行线的科学的方法呢?三、探索园我们发现,两条直线被第三条直线所截,只要保持同位角不变,画出的直线就平行于已知直线。这就是说:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简单的说,就是:同位角相等,两直线平行。即在图2中直线a、b被直线c所截,如果∠1=∠2,那么a∥b 。三、探索园例1、 如图3,直线a、b被直线c所截,已知∠1=115°,
∠2=115°,直线a、b平行吗?为什么? 注:这是一种新题型,我们应该先做判别,然后再用
因为……,所以……,证明你的观点。本题中,直线a与b平行。 解: 因为 ∠1=115°,∠2=115°(已知)
所以 ∠1=∠2(等量代换)
所以a∥b(同位角相等,两直线平行)图3四、实践园练习1:如图5,如果∠B=∠1,那么根据_________________,
可得AD∥BC;
如果∠D=∠1,那么根据 ________________,
可得AB∥CD.图5同位角相等,两直线平行内错角相等,两直线平行例2、如图6,在四边形ABCD中 ,已知∠B=60°∠C=120°,
AB与CD平行吗?AD与BC平行吗?四、实践园
解:本题中,直线AB与CD平行,
但根据题目的已知条件,
无法判定 AD与BC平行。
因为∠B=60°,∠C=120°(已知)
所以∠B+∠C=180°(等式性质)
所以AB∥CD(同旁内角互补,两直线平行)图6四、实践园练习2:如图7,
(1)如果,∠BAD+∠ABC=180°,那么根据同旁内角互补,
两直线平行,可得_____∥_____;
(2)如果,∠BCD+∠ABC=180°,那么根据同旁内角互补,
两直线平行,可得____∥____.图7AD BCAB CD四、实践园如图8:
(1)由∠B=∠6,可判定 ∥ ,
理由是 。
(2)∠B+∠BAD=180°,
可判定 ∥ ,理由是 。
(3)∠B+∠BED=180°,
可判定 ∥ ,理由是 。
(4)由∠3=∠2,可判定 ∥ ,
理由是 。
(5)由∠4=∠1,可判定 ∥ ,
理由是 。
(6)由∠4=∠7,可判定 ∥ ,
理由是 。
(7)由∠C=∠2,可判定 ∥ ,理由是 。
(8)由∠C+∠CDA=180°, 可判定 ∥ ,理由是 。AB DEAD BEAB DEAD BEAB DEAE CDAE CDAD BC四、实践园练习3(游戏)(每组派一名代表上讲台来写,看谁写得又对又多)使用直尺、三角尺或量角器,在图9(下图)上找出互相平行的直线和互相垂直的直线. 完整答案:互相垂直:互相平行:分别观察以下规律:①a⊥c,a⊥b,b∥c;②m⊥l,m⊥n,l∥n③ m ⊥l, d ⊥l ,d∥m。你能总结出这个规律吗?结论:如果两条直线都和第三条直线垂直,
那么这两条直线会平行。五、我们学到了什么5、垂直于同一条直线的两条直线互相平行;6、平行于同一条直线的两条直线互相平行。识别平行线的方法:1、平行线的定义:在同一平面内不相交得两条直线。2、同位角相等,两直线平行;3、内错角相等,两直线平行;4、同旁内角互补,两直线平行;例:图11中,a ⊥ c,b ⊥c,则有a∥b例:图12中,a ∥ c,b ∥c,则有a∥b如图13,直线EF分别与直线AB、CD相交于点P和点Q,
PQ平分∠APQ,QH平分∠DQP,并且∠1=∠2,
你能判定图中哪些直线平行?请说明理由。 课后练习:课本P172,练习第4题
同步测评以及轻巧夺冠(银版)的相关练习课后作业:P176 习题4.8 第3、4题谢谢观赏!
1、任何两条不相交的直线,叫做平行线.
2、已知直线a,则a的平行线只有1条.
3、在同一平面内,如果直线a与直线b无交点,直线b与直线c无交点,则直线a与直线c平行. 二、我们的问题:请观察右边图中的两条直线a和直线b,它们是什么位置关系?是相交?还是平行呢,你通过什么来判断的?ab显然,我们无法通过眼睛来直接判断,因为眼睛只是一个直观上的判断,那么我们能不能找到一种可以有效识别平行线的科学的方法呢?三、探索园我们发现,两条直线被第三条直线所截,只要保持同位角不变,画出的直线就平行于已知直线。这就是说:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。简单的说,就是:同位角相等,两直线平行。即在图2中直线a、b被直线c所截,如果∠1=∠2,那么a∥b 。三、探索园例1、 如图3,直线a、b被直线c所截,已知∠1=115°,
∠2=115°,直线a、b平行吗?为什么? 注:这是一种新题型,我们应该先做判别,然后再用
因为……,所以……,证明你的观点。本题中,直线a与b平行。 解: 因为 ∠1=115°,∠2=115°(已知)
所以 ∠1=∠2(等量代换)
所以a∥b(同位角相等,两直线平行)图3四、实践园练习1:如图5,如果∠B=∠1,那么根据_________________,
可得AD∥BC;
如果∠D=∠1,那么根据 ________________,
可得AB∥CD.图5同位角相等,两直线平行内错角相等,两直线平行例2、如图6,在四边形ABCD中 ,已知∠B=60°∠C=120°,
AB与CD平行吗?AD与BC平行吗?四、实践园
解:本题中,直线AB与CD平行,
但根据题目的已知条件,
无法判定 AD与BC平行。
因为∠B=60°,∠C=120°(已知)
所以∠B+∠C=180°(等式性质)
所以AB∥CD(同旁内角互补,两直线平行)图6四、实践园练习2:如图7,
(1)如果,∠BAD+∠ABC=180°,那么根据同旁内角互补,
两直线平行,可得_____∥_____;
(2)如果,∠BCD+∠ABC=180°,那么根据同旁内角互补,
两直线平行,可得____∥____.图7AD BCAB CD四、实践园如图8:
(1)由∠B=∠6,可判定 ∥ ,
理由是 。
(2)∠B+∠BAD=180°,
可判定 ∥ ,理由是 。
(3)∠B+∠BED=180°,
可判定 ∥ ,理由是 。
(4)由∠3=∠2,可判定 ∥ ,
理由是 。
(5)由∠4=∠1,可判定 ∥ ,
理由是 。
(6)由∠4=∠7,可判定 ∥ ,
理由是 。
(7)由∠C=∠2,可判定 ∥ ,理由是 。
(8)由∠C+∠CDA=180°, 可判定 ∥ ,理由是 。AB DEAD BEAB DEAD BEAB DEAE CDAE CDAD BC四、实践园练习3(游戏)(每组派一名代表上讲台来写,看谁写得又对又多)使用直尺、三角尺或量角器,在图9(下图)上找出互相平行的直线和互相垂直的直线. 完整答案:互相垂直:互相平行:分别观察以下规律:①a⊥c,a⊥b,b∥c;②m⊥l,m⊥n,l∥n③ m ⊥l, d ⊥l ,d∥m。你能总结出这个规律吗?结论:如果两条直线都和第三条直线垂直,
那么这两条直线会平行。五、我们学到了什么5、垂直于同一条直线的两条直线互相平行;6、平行于同一条直线的两条直线互相平行。识别平行线的方法:1、平行线的定义:在同一平面内不相交得两条直线。2、同位角相等,两直线平行;3、内错角相等,两直线平行;4、同旁内角互补,两直线平行;例:图11中,a ⊥ c,b ⊥c,则有a∥b例:图12中,a ∥ c,b ∥c,则有a∥b如图13,直线EF分别与直线AB、CD相交于点P和点Q,
PQ平分∠APQ,QH平分∠DQP,并且∠1=∠2,
你能判定图中哪些直线平行?请说明理由。 课后练习:课本P172,练习第4题
同步测评以及轻巧夺冠(银版)的相关练习课后作业:P176 习题4.8 第3、4题谢谢观赏!
