等式的性质[上学期]

课件16张PPT。等 式 的 性 质复 习方程：含有未知数的等式。一元一次方程：方程中只含有一个未知数（元）x，未知数的指数都是1（次）.解方程：求出使方程中等号左右两边相等的未知数的值.
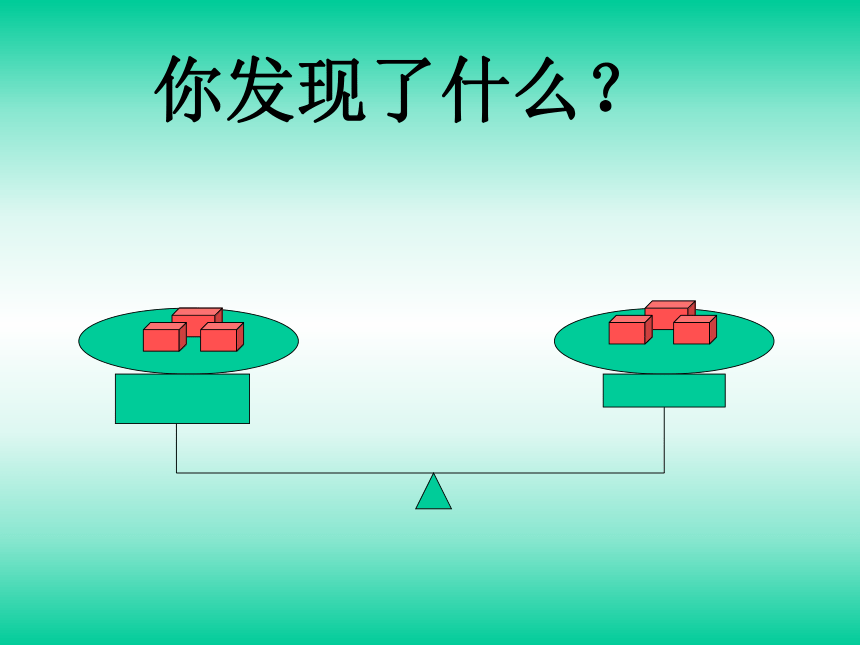
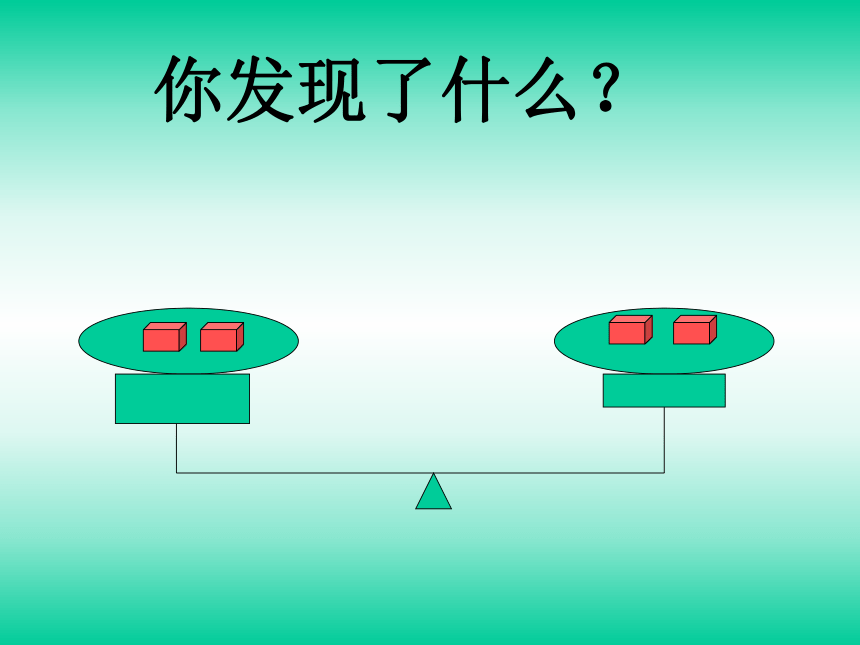
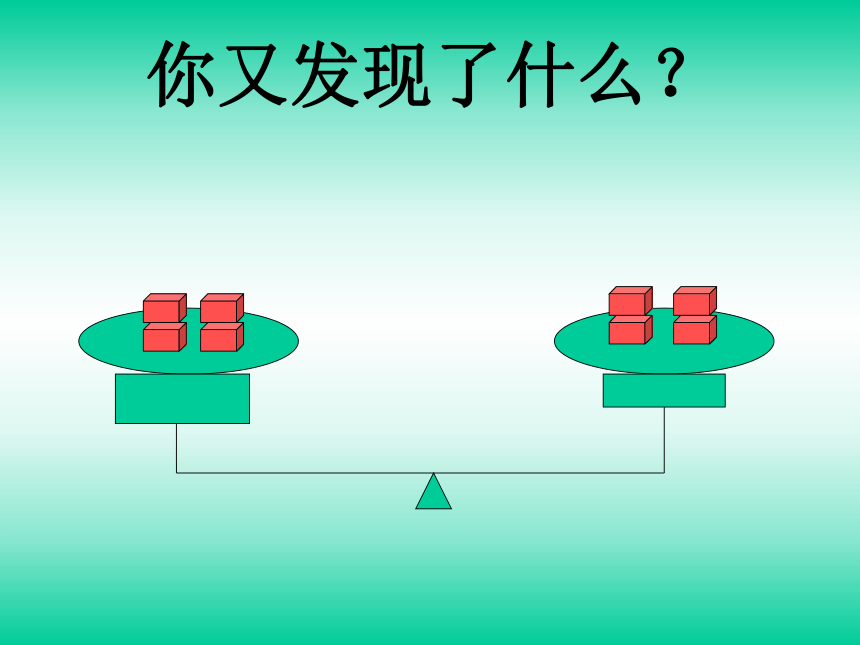
方程的解:使方程左右两边相等的未知数的值.你能猜想方程- x+ =- 的解吗?X=? 像这样用等号“=”来表示相等关系的式子叫作等式．左边右边你发现了什么？你发现了什么？你又发现了什么？你又发现了什么？等式性质1 等式两边加(或减)同一个数(或式子)，结
果仍相等。等式性质2 等式两边乘同一个数,或除以同一个不为0
的数，结果仍相等。 如果a=b，那么a±c= 。 b±c bc分析：要使方程x+7=26转化为x=a(常数)的形式，要去掉方程左边的7，因
此两边要减7。你会类似的考虑另两个方程如何转化为x=a的形式吗？（1）两边减7，得

x+7-7=26-7 于是
x=19.解：例2 利用等式的性质解下列方程：
（1）x+7=26； （2）-5x=20； （3）- x-5=4。检验:把方程的解代入原方程,看这个值能否使方程的两边相等。检验：将x=19代入方程x+7=26的左边，得
19+7=26
左边=右边，所以x=19是方程的解。于是
x= - 4 .两边同乘-3，得
x=-27检验：将x=-4代入方程-5x=20
的左边，得
-5×（-4）=20
左边=右边，所以x=-4是方程的解。解：两边加5，得

- x-5+5=4+5 化简，得
- x=9检验：将x=-27代入方程
- x-5=4的左边，得
- ×（-27）-5=4
左边=右边，所以x=-27是方程的解。
（2）-5x=20；（3）- x-5=4解：两边同除以-5，得

= （1）两边同加5，得0.3x÷ 0.3=45÷ 0.3x-5+5 =6 +5于是 x=11（2）两边同除以0.3，得于是 x=150解：★练 习★
利用等式的性质解下列方程并检验：
(1)x-5=6； （2）0.3x=45；
（3）2- x=3； （4）5x+4=0 （3）两边同减2，得5x+4- 4=0-4（4）两边同减4，得解：两边同乘以-4，得
x=-4化简，得
5x=-42- x-2=3-2化简，得
- x=1 两边同乘以5，得
x=-运用等式的性质时应注意：1、等式的左右两边参加同一种运算；2、等式的左右两边加、减、乘、除的数一定是同一个数或式子；3、不能都除以0，0不能作除数或分母；☆练 习☆用等式的性质求x（1）x-4=29；
（2） x+2=6；
（3）3x+1=4；
（4）4x-2=2.作 业：
☆(1) 课本P75 4题

☆(2) 同步练习