三角形的内切圆[上学期]
图片预览

文档简介
课件18张PPT。三角形的内切圆1、确定圆的条件是什么?1.圆心与半径2、叙述角平线的性质与判定性质:角平线上的点到这个角的两边的距离相等。
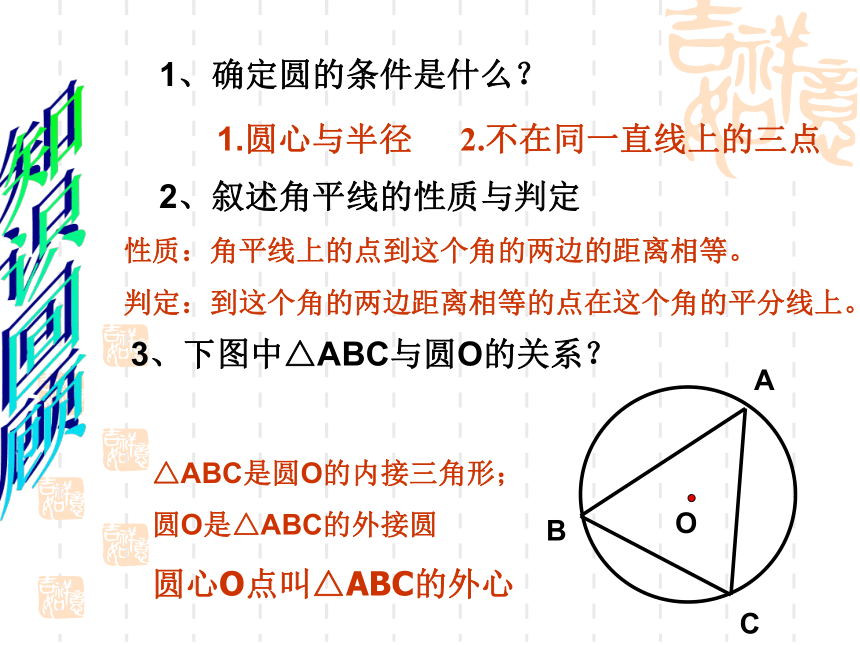
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
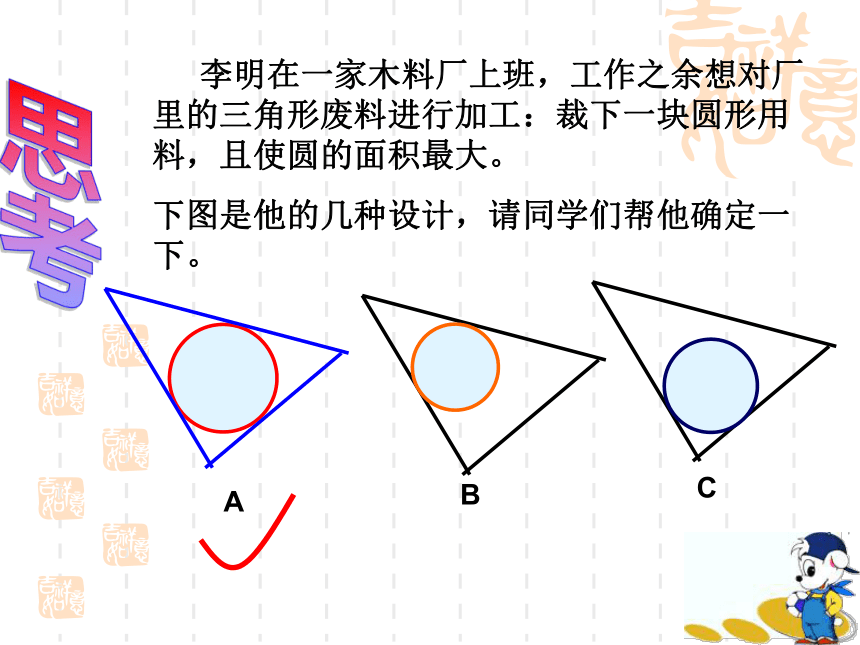
圆心O点叫△ABC的外心知识回顾2.不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
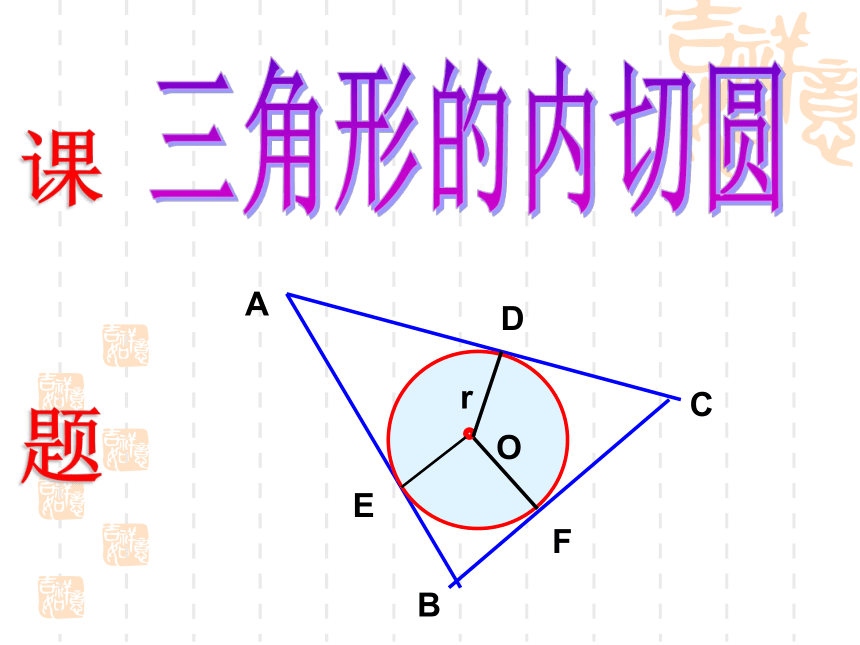
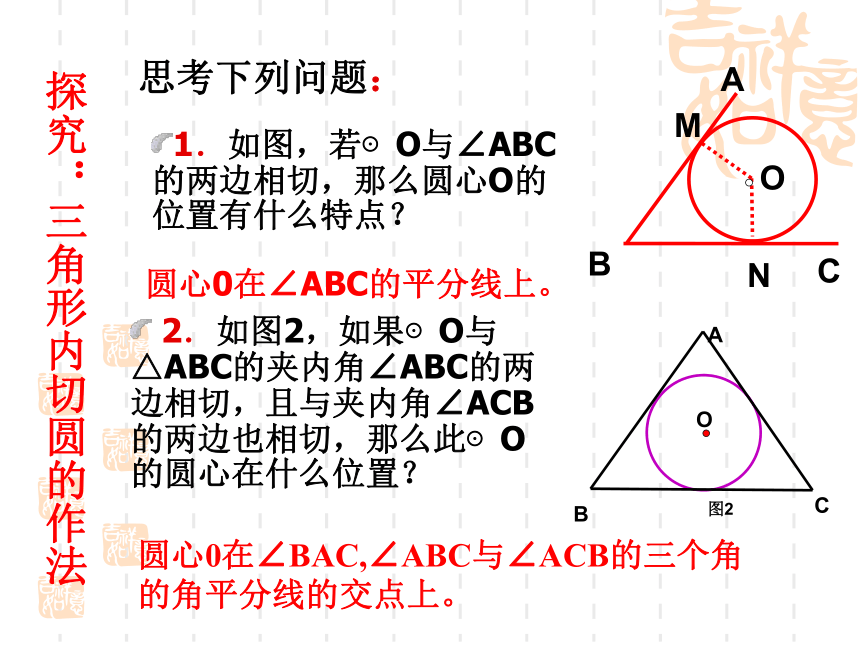
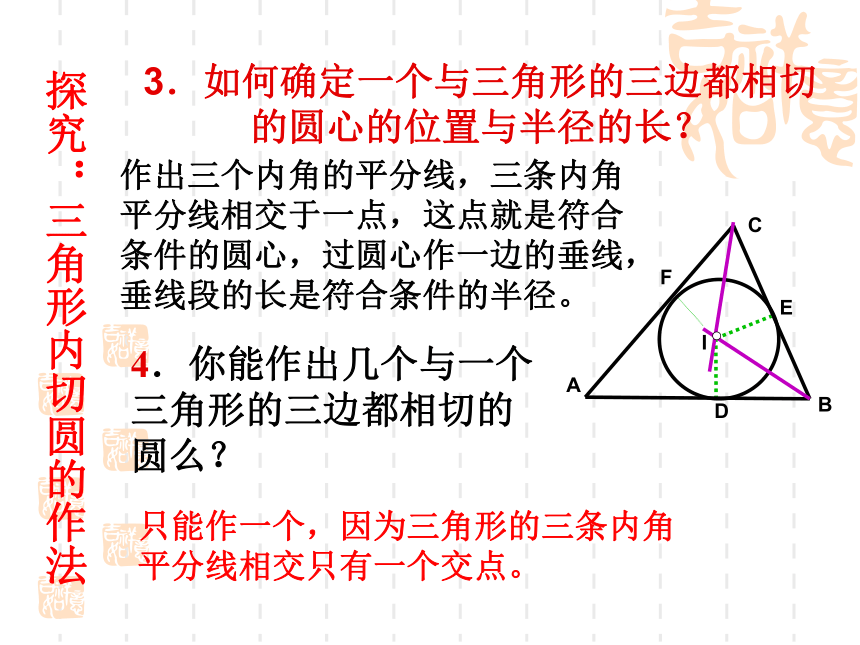
下图是他的几种设计,请同学们帮他确定一下。思考ABC三角形的内切圆Or课 题思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的夹内角∠ABC的两边相切,且与夹内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形的三边都相切的圆心的位置与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,因为三角形的三条内角
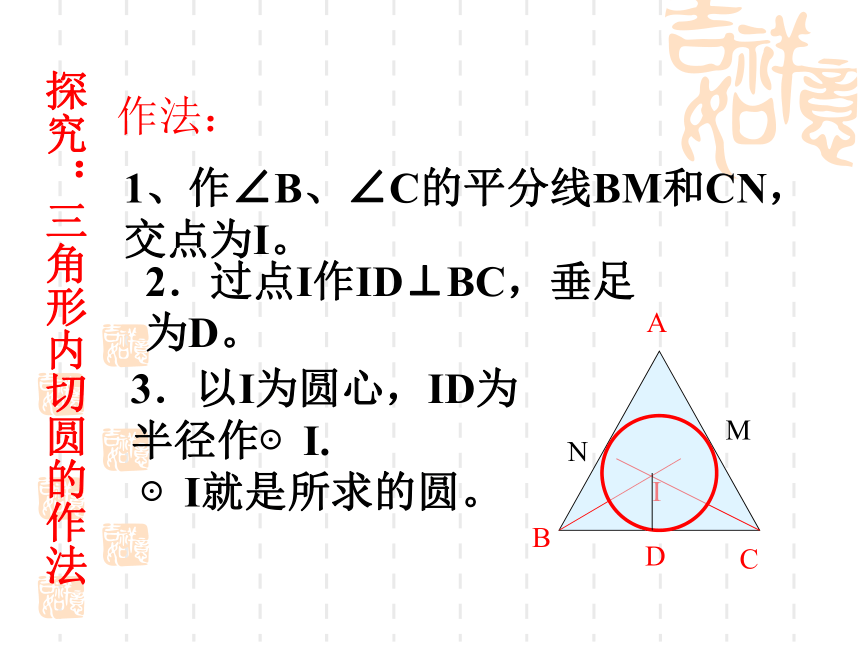
平分线相交只有一个交点。 IFCABED探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN探究:三角形内切圆的作法1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。识记2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。?
外心(三角形外接圆的圆心)
?
例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠2)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50
C三角形内心性质的应用例2、求等边三角形的内切圆半径r与
外接圆半径R的比。解:由等腰三角形底边上的中垂线与顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆设内切圆切BC于D,连接OB,OD于是就有sin∠OBD=sin30°=
知 识 的 应 用已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。引 例解:因为△ABC的内切圆分别和BC、AC、AB切于点D、E、F,由切线长定理知AE=AF,CE=CD,BD=BF∴AF+BD+CE= (AB+AC+BC)∵BD+CE=∴AF=13-9=4BD+CD=BC=9=13知 识 的 应 用r如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为:2cm练习2、圆内接平行四边形是矩形圆外切平行四边形是_______D延伸与拓展菱形1、判断:
如图:1、△ABC是圆O的外切三角形。( )
2、圆O是△ABC的外接圆。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCO检测已知:△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
ABCDE补充练习
判定:到这个角的两边距离相等的点在这个角的平分线上。3、下图中△ABC与圆O的关系?△ABC是圆O的内接三角形;
圆O是△ABC的外接圆
圆心O点叫△ABC的外心知识回顾2.不在同一直线上的三点 李明在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。思考ABC三角形的内切圆Or课 题思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的夹内角∠ABC的两边相切,且与夹内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN探究:三角形内切圆的作法3.如何确定一个与三角形的三边都相切的圆心的位置与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆么? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,因为三角形的三条内角
平分线相交只有一个交点。 IFCABED探究:三角形内切圆的作法作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN探究:三角形内切圆的作法1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。识记2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。?
外心(三角形外接圆的圆心)
?
例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠2)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50
C三角形内心性质的应用例2、求等边三角形的内切圆半径r与
外接圆半径R的比。解:由等腰三角形底边上的中垂线与顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆设内切圆切BC于D,连接OB,OD于是就有sin∠OBD=sin30°=
知 识 的 应 用已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。引 例解:因为△ABC的内切圆分别和BC、AC、AB切于点D、E、F,由切线长定理知AE=AF,CE=CD,BD=BF∴AF+BD+CE= (AB+AC+BC)∵BD+CE=∴AF=13-9=4BD+CD=BC=9=13知 识 的 应 用r如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。如图:直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径为:2cm练习2、圆内接平行四边形是矩形圆外切平行四边形是_______D延伸与拓展菱形1、判断:
如图:1、△ABC是圆O的外切三角形。( )
2、圆O是△ABC的外接圆。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCO检测已知:△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
ABCDE补充练习
