三角形的外角(一)[下学期]
文档属性
| 名称 | 三角形的外角(一)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 44.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-09 12:45:00 | ||
图片预览

文档简介
三角形的外角(一)
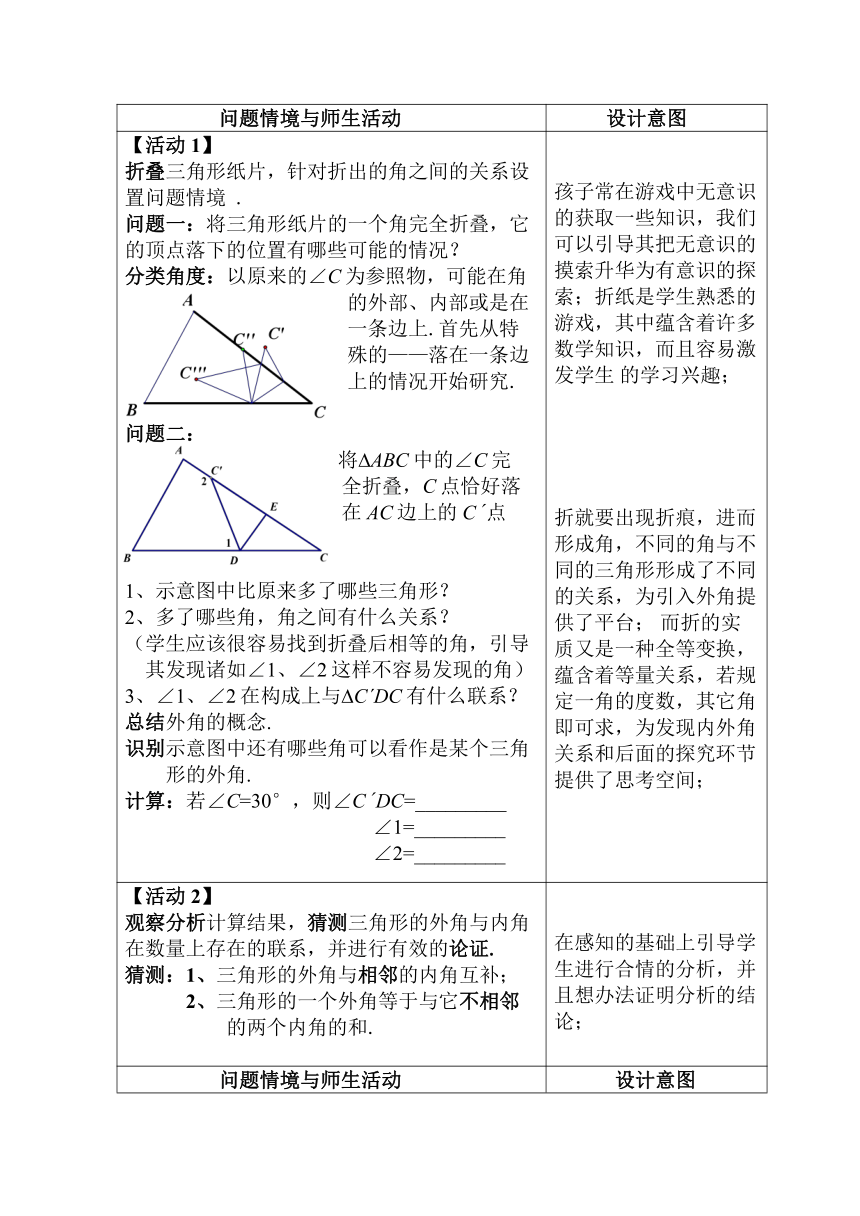
教学任务分析:
教学目标预定 知识技能 1、理解三角形外角的概念;2、在探索中掌握三角形外角与内角的关系;3、综合运用三角形内、外角知识解决特定的数学问题.
数学思考 1、在猜想、论证过程中体会知识间的区别与联系;2、抓住实质,从不同角度思考解决问题的方法;3、有效利用转化思想,将复杂图形简单化,有意识的优化解决策略.
解决问题 尝试从实际情境中抽取信息、形成数学思考,从中获得解决与角度有关的计算和角的关系问题的一点经验,并体会解决策略的多样性,增强对图形的辨析能力.
情感态度 在共同活动中培养数学兴趣和合作学习能力,在探索过程中培养创新意识,体会数学知识的内在联系,追求和谐美、简洁美.
重点 三角形内、外角关系及其应用
难点估计 复杂图形的分析与内、外角关系的灵活应用.
课前准备
教具 学具 所需预备知识
课件、三角形纸片 三角形纸片、学案 三角形内角和、平行线等.
教学流程大致安排
师生互动流程图 活动内容和目的
【活动1】在活动中理解三角形的外角 由折纸活动引出研究课题,抽象出三角形外角的概念,直观感觉内、外角的关系.
【活动2】猜测、验证三角形内、外角的关系 在直觉的基础上进行有效的数学验证,由方法的多样性培养发散性思维能力.
【活动3】 练习 加深对三角形内、外角关系的理解,能在复合图形中应用其进行简单计算.
【活动4】折纸问题再研究 探究【活动1】折纸的其它情况,学会将复杂图形转化成基本图形,解析复杂的角的关系问题,体会知识内在的发展联系.
【活动5】小结 简要回顾所学知识,体会外角的引进对于优化解题策略的贡献.
【活动6】思考 充分挖掘折纸中的隐含条件,并结合内、外角知识探索综合问题.
教学过程设计:
问题情境与师生活动 设计意图
【活动1】折叠三角形纸片,针对折出的角之间的关系设置问题情境 .问题一:将三角形纸片的一个角完全折叠,它的顶点落下的位置有哪些可能的情况? 分类角度:以原来的∠C为参照物,可能在角的外部、内部或是在一条边上.首先从特殊的——落在一条边上的情况开始研究.问题二: 将 ABC中的∠C完全折叠,C点恰好落在AC边上的C 点1、示意图中比原来多了哪些三角形?2、多了哪些角,角之间有什么关系? (学生应该很容易找到折叠后相等的角,引导其发现诸如∠1、∠2这样不容易发现的角)3、∠1、∠2在构成上与 C DC有什么联系? 总结外角的概念.识别示意图中还有哪些角可以看作是某个三角形的外角.计算:若∠C=30°,则∠C DC=_________ ∠1=_________ ∠2=_________ 孩子常在游戏中无意识的获取一些知识,我们可以引导其把无意识的摸索升华为有意识的探索;折纸是学生熟悉的游戏,其中蕴含着许多数学知识,而且容易激发学生 的学习兴趣;折就要出现折痕,进而形成角,不同的角与不同的三角形形成了不同的关系,为引入外角提供了平台; 而折的实质又是一种全等变换,蕴含着等量关系,若规定一角的度数,其它角即可求,为发现内外角关系和后面的探究环节提供了思考空间;
【活动2】观察分析计算结果,猜测三角形的外角与内角在数量上存在的联系,并进行有效的论证.猜测:1、三角形的外角与相邻的内角互补; 2、三角形的一个外角等于与它不相邻的两个内角的和. 在感知的基础上引导学生进行合情的分析,并且想办法证明分析的结论;
问题情境与师生活动 设计意图
验证:结论1由互为邻补角的概念即可知;结论2 : 已知:∠ACD为 ABC的外角 求证:∠ACD=∠A+∠B 方案一:在 ABC中∠A+∠B=180°-∠ACB又∵B、C、D共线∴∠ACD=180°-∠ACB∴∠ACD=∠A+∠B方案二:引导学生构造图形解决问题大致方法: 等. 证明方法具有多样性,培养学生发散性思维;但目的还在于让学生体会:“看清问题的实质是什么——我们学过的哪些知识能提供思路——选择哪条、怎样操作”这样一个解决问题的一般程序.我们的思路:利用平行线将某些角移动到便于我们证明的位置,从而解决问题.
【活动3】结论的简单应用说出下列图形中各角的度数: 此组题就结论进行简单训练;会在常见的复合图形中识别三角形的外角,有意识的应用其进行简单角度计算.
【活动4】思考:刚才折叠三角形时的另外两种情况:情况一:点C在参照物外部,探究示意图中∠1、∠2、∠C的关系. 关注∠1、∠2 作为外角的特殊位置(∠1+∠2=2∠C) 折纸问题是今后学习中,几何情境设置的常用素材;此活动意在提
问题情境与师生活动 设计意图
情况二:点C在参照物内部,再探究示意图中∠1、∠2与∠C的关系. 分析:从学生已有的知识和经验考虑,应该能找到诸如“∠1、∠2分别与旁边的角互补,结合折叠角的相等及三角形内角和推导”“∠1、∠2分别与旁边的角互补,结合四边形内角和推导”等方法.但由∠1、∠2的位置容易联想到它们可能是某些三角形的外角,所以引导学生添加辅助线将∠C转化到以∠1、∠2为外角的两个三角形中去,从而解决问题. (∠1+∠2 =2∠C) 升对问题的发展变化全面系统思考的分析能力,和利用转化思想灵活解决问题的能力;另外通过各种解决方法的比较突显外角知识应用所带来的便捷性.
【活动5】 小结:外角概念;三角形内、外角的关系及其在几何图形中的转化、应用. 重在体会外角知识在优化解题方法上的作用.
【活动6】再将三角形进行新的折叠: 把∠B的两边重合,留下折痕,再把∠C的两边重合,留下折痕,探究两道折痕的夹角∠1与∠A的关系.挖掘隐含条件:对折的折痕即是角平分线;利用三角形内角和将∠FBC+∠FCB表示成∠A的代数式;而∠1又是 FBC的外角. ( ) 进一步思考:其它条件不变的情况下,连结AF,并作FG⊥AB,∠1与∠2什么关系? (留为作业) 贯穿折纸的线索,充分挖掘折纸中的隐含条件,并结合内、外角知识探索综合问题,提升解决问题的能力;另外由两层问题的思考引导学生观察图形间的联系与区别,加强对基本模型的认识,和对基本模型的转化、利用的意识,为今后探究几何问题提供一种可借鉴的做法和模式.
三角形的外角(一)
北京市海淀实验中学 王靓
2006年4月
教学任务分析:
教学目标预定 知识技能 1、理解三角形外角的概念;2、在探索中掌握三角形外角与内角的关系;3、综合运用三角形内、外角知识解决特定的数学问题.
数学思考 1、在猜想、论证过程中体会知识间的区别与联系;2、抓住实质,从不同角度思考解决问题的方法;3、有效利用转化思想,将复杂图形简单化,有意识的优化解决策略.
解决问题 尝试从实际情境中抽取信息、形成数学思考,从中获得解决与角度有关的计算和角的关系问题的一点经验,并体会解决策略的多样性,增强对图形的辨析能力.
情感态度 在共同活动中培养数学兴趣和合作学习能力,在探索过程中培养创新意识,体会数学知识的内在联系,追求和谐美、简洁美.
重点 三角形内、外角关系及其应用
难点估计 复杂图形的分析与内、外角关系的灵活应用.
课前准备
教具 学具 所需预备知识
课件、三角形纸片 三角形纸片、学案 三角形内角和、平行线等.
教学流程大致安排
师生互动流程图 活动内容和目的
【活动1】在活动中理解三角形的外角 由折纸活动引出研究课题,抽象出三角形外角的概念,直观感觉内、外角的关系.
【活动2】猜测、验证三角形内、外角的关系 在直觉的基础上进行有效的数学验证,由方法的多样性培养发散性思维能力.
【活动3】 练习 加深对三角形内、外角关系的理解,能在复合图形中应用其进行简单计算.
【活动4】折纸问题再研究 探究【活动1】折纸的其它情况,学会将复杂图形转化成基本图形,解析复杂的角的关系问题,体会知识内在的发展联系.
【活动5】小结 简要回顾所学知识,体会外角的引进对于优化解题策略的贡献.
【活动6】思考 充分挖掘折纸中的隐含条件,并结合内、外角知识探索综合问题.
教学过程设计:
问题情境与师生活动 设计意图
【活动1】折叠三角形纸片,针对折出的角之间的关系设置问题情境 .问题一:将三角形纸片的一个角完全折叠,它的顶点落下的位置有哪些可能的情况? 分类角度:以原来的∠C为参照物,可能在角的外部、内部或是在一条边上.首先从特殊的——落在一条边上的情况开始研究.问题二: 将 ABC中的∠C完全折叠,C点恰好落在AC边上的C 点1、示意图中比原来多了哪些三角形?2、多了哪些角,角之间有什么关系? (学生应该很容易找到折叠后相等的角,引导其发现诸如∠1、∠2这样不容易发现的角)3、∠1、∠2在构成上与 C DC有什么联系? 总结外角的概念.识别示意图中还有哪些角可以看作是某个三角形的外角.计算:若∠C=30°,则∠C DC=_________ ∠1=_________ ∠2=_________ 孩子常在游戏中无意识的获取一些知识,我们可以引导其把无意识的摸索升华为有意识的探索;折纸是学生熟悉的游戏,其中蕴含着许多数学知识,而且容易激发学生 的学习兴趣;折就要出现折痕,进而形成角,不同的角与不同的三角形形成了不同的关系,为引入外角提供了平台; 而折的实质又是一种全等变换,蕴含着等量关系,若规定一角的度数,其它角即可求,为发现内外角关系和后面的探究环节提供了思考空间;
【活动2】观察分析计算结果,猜测三角形的外角与内角在数量上存在的联系,并进行有效的论证.猜测:1、三角形的外角与相邻的内角互补; 2、三角形的一个外角等于与它不相邻的两个内角的和. 在感知的基础上引导学生进行合情的分析,并且想办法证明分析的结论;
问题情境与师生活动 设计意图
验证:结论1由互为邻补角的概念即可知;结论2 : 已知:∠ACD为 ABC的外角 求证:∠ACD=∠A+∠B 方案一:在 ABC中∠A+∠B=180°-∠ACB又∵B、C、D共线∴∠ACD=180°-∠ACB∴∠ACD=∠A+∠B方案二:引导学生构造图形解决问题大致方法: 等. 证明方法具有多样性,培养学生发散性思维;但目的还在于让学生体会:“看清问题的实质是什么——我们学过的哪些知识能提供思路——选择哪条、怎样操作”这样一个解决问题的一般程序.我们的思路:利用平行线将某些角移动到便于我们证明的位置,从而解决问题.
【活动3】结论的简单应用说出下列图形中各角的度数: 此组题就结论进行简单训练;会在常见的复合图形中识别三角形的外角,有意识的应用其进行简单角度计算.
【活动4】思考:刚才折叠三角形时的另外两种情况:情况一:点C在参照物外部,探究示意图中∠1、∠2、∠C的关系. 关注∠1、∠2 作为外角的特殊位置(∠1+∠2=2∠C) 折纸问题是今后学习中,几何情境设置的常用素材;此活动意在提
问题情境与师生活动 设计意图
情况二:点C在参照物内部,再探究示意图中∠1、∠2与∠C的关系. 分析:从学生已有的知识和经验考虑,应该能找到诸如“∠1、∠2分别与旁边的角互补,结合折叠角的相等及三角形内角和推导”“∠1、∠2分别与旁边的角互补,结合四边形内角和推导”等方法.但由∠1、∠2的位置容易联想到它们可能是某些三角形的外角,所以引导学生添加辅助线将∠C转化到以∠1、∠2为外角的两个三角形中去,从而解决问题. (∠1+∠2 =2∠C) 升对问题的发展变化全面系统思考的分析能力,和利用转化思想灵活解决问题的能力;另外通过各种解决方法的比较突显外角知识应用所带来的便捷性.
【活动5】 小结:外角概念;三角形内、外角的关系及其在几何图形中的转化、应用. 重在体会外角知识在优化解题方法上的作用.
【活动6】再将三角形进行新的折叠: 把∠B的两边重合,留下折痕,再把∠C的两边重合,留下折痕,探究两道折痕的夹角∠1与∠A的关系.挖掘隐含条件:对折的折痕即是角平分线;利用三角形内角和将∠FBC+∠FCB表示成∠A的代数式;而∠1又是 FBC的外角. ( ) 进一步思考:其它条件不变的情况下,连结AF,并作FG⊥AB,∠1与∠2什么关系? (留为作业) 贯穿折纸的线索,充分挖掘折纸中的隐含条件,并结合内、外角知识探索综合问题,提升解决问题的能力;另外由两层问题的思考引导学生观察图形间的联系与区别,加强对基本模型的认识,和对基本模型的转化、利用的意识,为今后探究几何问题提供一种可借鉴的做法和模式.
三角形的外角(一)
北京市海淀实验中学 王靓
2006年4月
