19.1.2 函数的图象 教案 课时 2
文档属性
| 名称 | 19.1.2 函数的图象 教案 课时 2 |

|
|
| 格式 | doc | ||
| 文件大小 | 319.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-29 17:45:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章 一次函数 教案
19.1.2函数的图象
第2课时
教学目标:
确地运用列表、描点、连线等步骤画出函数的图象.理解并掌握函数的不同表示方法,会发现函数图象所提供的信息.
重点:
函数图象的画法.
难点:
从图象中提取信息,利用图象解决问题.
教学流程:
一、导入新课
问题:什么是函数的图象?
答案:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
二、新课讲解
引言:如何画函数的图象呢?
例1:下列式子中,对于 x 每一个确定的值,y 有唯一的对应值,即 y 是x的函数,请画出这些函数的图象.
(1)y=x+0.5;
解:(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点用平滑的曲线连接起来.
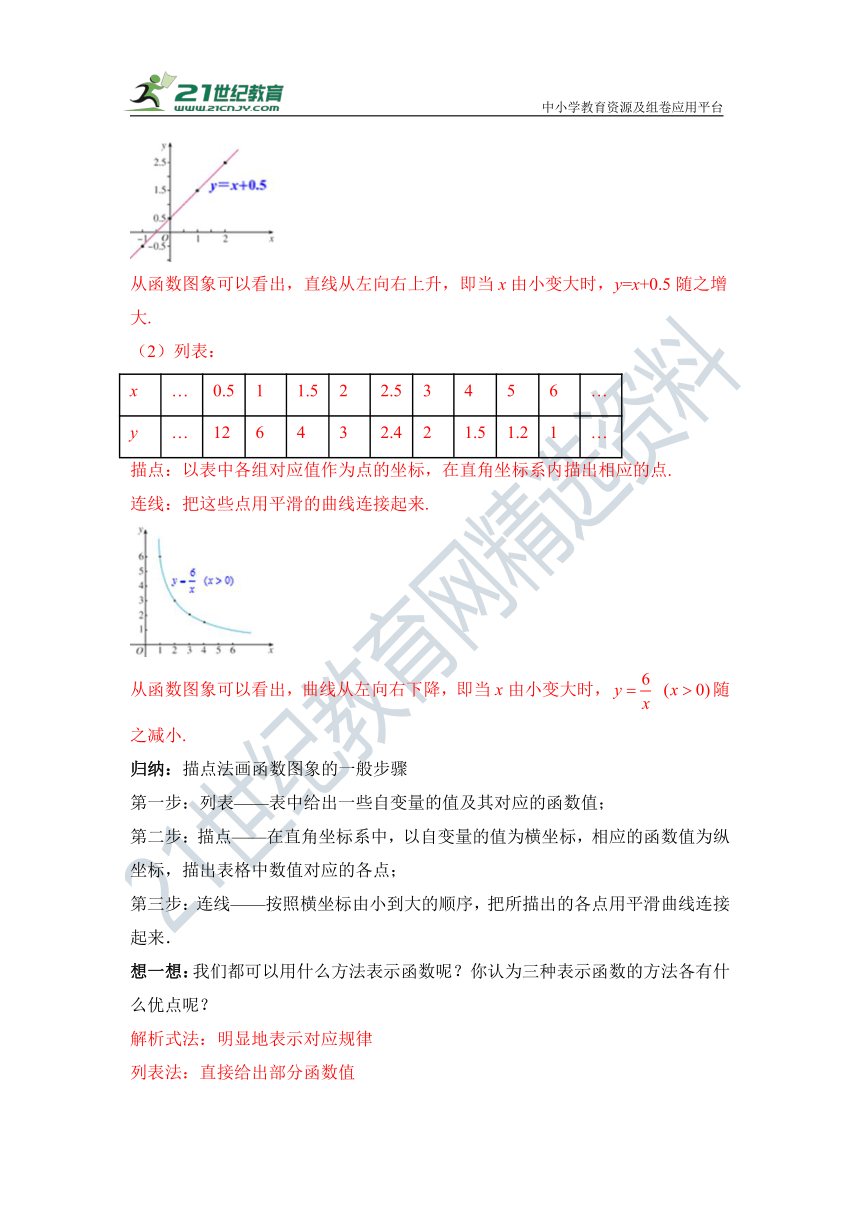
从函数图象可以看出,直线从左向右上升,即当x由小变大时,y=x+0.5随之增大.
(2)列表:
x … 0.5 1 1.5 2 2.5 3 4 5 6 …
y … 12 6 4 3 2.4 2 1.5 1.2 1 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点用平滑的曲线连接起来.
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,随之减小.
归纳:描点法画函数图象的一般步骤
第一步:列表——表中给出一些自变量的值及其对应的函数值;
第二步:描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线——按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
想一想:我们都可以用什么方法表示函数呢?你认为三种表示函数的方法各有什么优点呢?
解析式法:明显地表示对应规律
列表法:直接给出部分函数值
图象法:直观地表示变化趋势
例2:一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少米.
解:(1)如图,描出上表中数据对应的点.可以看出,这6个点在一条直线上.再结合表中数据,可以发现每小时水位上升0. 3m.
由此猜想,如果画出这5h内其他时刻(如t=2. 5h等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度匀速上升的.
(2)如果在这5h内,水位一直匀速上升,即升速为0. 3m/h,那么函数y=0.3t+3 (0≤t ≤ 5)就精确地表示了这种变化规律.即使在这5h内,水位的升速有些变化,而由于每小时水位上升0.3m是确定的,因此这个函数可以近似地表示水位的变化规律.
(3)如果水位的变化规律不变,则可利用上述函数预测,再过2h,即t=5+2=7(h)时,水位高度y=0. 3× 7+3=5. 1(m).
把图中的函数图象(线段AB)向右延伸到t=7所对应的位置,也能看出这时的水位高度约为5. lm.
强调:由例题可以看出,函数的不同表示法之间可以转化.
三、巩固提升
1.在某次实验中,测得两个变量m与v之间的4组对应数据如下表,则m与v之间的关系最接近于下列各关系式中的( )
m 1 2 3 4
v 0.01 2.9 8.03 15.1
A. v=2m-2 B. v=m2-1 C. v=3m-3 D. v=m+1
答案:B
2.如图,OA,BA分别表示甲、乙两名学生匀速跑步运动的函数图象,图中s和t分别表示运动路程和时间.根据图象判断跑步快者比慢者每秒快____m.
答案:1.5
3.已知函数y=2x-1.
(1)填表:
x … -2 -1 0 1 2 …
y … …
(2)画出函数y=2x-1的图象.
(3)判断点A(-3,-5),B(2,-3),C(3,5)是否在函数y=2x-1的图象上;
(4)若点P(m,9)在函数y=2x-1的图象上,求出m的值.
答案:(1)-5,-3,-1,1,3
(2)函数图象如图所示
(3)当x=3时,y=2×(-3)-1=-7,
∴点A不在函数y=2x-1的图象上;
当x=2时,y=2×2-1=3,
∴点B不在函数y=2x-1的图象上;
当x=3时,y=2×3-1=5,
∴点C在函数y=2x-1的图象上.
(4)∵点P(m,9)在函数y=2x-1的图象上,
∴2m-1=9,
解得:m=5.
4.下表是丽丽往姥姥家打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)如果用x表示时间,y表示电话费,上表反映了哪两个变量之间的关系?请用式子表示它们的关系.
(2)随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
(4)你能帮丽丽预测一下,如果打10分钟的电话,需付多少元话费?
解:(1)电话费与时间之间的关系,y=0.6x
(2)随x的增大,y也随之增大.
(3)当x=5时,y=0.6×5=3(元)
(4)当x=10时,y=0.6×10=6(元)
四、课堂小结
今天我们学习了哪些知识?
1.函数有哪几种表示方法?它们各有什么优点?
2.如何根据函数分析变量的变化规律和变化趋势?
五、布置作业
教材P80页练习题第3题.
第19章 一次函数 教案
19.1.2函数的图象
第2课时
教学目标:
确地运用列表、描点、连线等步骤画出函数的图象.理解并掌握函数的不同表示方法,会发现函数图象所提供的信息.
重点:
函数图象的画法.
难点:
从图象中提取信息,利用图象解决问题.
教学流程:
一、导入新课
问题:什么是函数的图象?
答案:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
二、新课讲解
引言:如何画函数的图象呢?
例1:下列式子中,对于 x 每一个确定的值,y 有唯一的对应值,即 y 是x的函数,请画出这些函数的图象.
(1)y=x+0.5;
解:(1)列表:
x … -3 -2 -1 0 1 2 3 …
y … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点用平滑的曲线连接起来.
从函数图象可以看出,直线从左向右上升,即当x由小变大时,y=x+0.5随之增大.
(2)列表:
x … 0.5 1 1.5 2 2.5 3 4 5 6 …
y … 12 6 4 3 2.4 2 1.5 1.2 1 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点用平滑的曲线连接起来.
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,随之减小.
归纳:描点法画函数图象的一般步骤
第一步:列表——表中给出一些自变量的值及其对应的函数值;
第二步:描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线——按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
想一想:我们都可以用什么方法表示函数呢?你认为三种表示函数的方法各有什么优点呢?
解析式法:明显地表示对应规律
列表法:直接给出部分函数值
图象法:直观地表示变化趋势
例2:一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象.这个函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少米.
解:(1)如图,描出上表中数据对应的点.可以看出,这6个点在一条直线上.再结合表中数据,可以发现每小时水位上升0. 3m.
由此猜想,如果画出这5h内其他时刻(如t=2. 5h等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度匀速上升的.
(2)如果在这5h内,水位一直匀速上升,即升速为0. 3m/h,那么函数y=0.3t+3 (0≤t ≤ 5)就精确地表示了这种变化规律.即使在这5h内,水位的升速有些变化,而由于每小时水位上升0.3m是确定的,因此这个函数可以近似地表示水位的变化规律.
(3)如果水位的变化规律不变,则可利用上述函数预测,再过2h,即t=5+2=7(h)时,水位高度y=0. 3× 7+3=5. 1(m).
把图中的函数图象(线段AB)向右延伸到t=7所对应的位置,也能看出这时的水位高度约为5. lm.
强调:由例题可以看出,函数的不同表示法之间可以转化.
三、巩固提升
1.在某次实验中,测得两个变量m与v之间的4组对应数据如下表,则m与v之间的关系最接近于下列各关系式中的( )
m 1 2 3 4
v 0.01 2.9 8.03 15.1
A. v=2m-2 B. v=m2-1 C. v=3m-3 D. v=m+1
答案:B
2.如图,OA,BA分别表示甲、乙两名学生匀速跑步运动的函数图象,图中s和t分别表示运动路程和时间.根据图象判断跑步快者比慢者每秒快____m.
答案:1.5
3.已知函数y=2x-1.
(1)填表:
x … -2 -1 0 1 2 …
y … …
(2)画出函数y=2x-1的图象.
(3)判断点A(-3,-5),B(2,-3),C(3,5)是否在函数y=2x-1的图象上;
(4)若点P(m,9)在函数y=2x-1的图象上,求出m的值.
答案:(1)-5,-3,-1,1,3
(2)函数图象如图所示
(3)当x=3时,y=2×(-3)-1=-7,
∴点A不在函数y=2x-1的图象上;
当x=2时,y=2×2-1=3,
∴点B不在函数y=2x-1的图象上;
当x=3时,y=2×3-1=5,
∴点C在函数y=2x-1的图象上.
(4)∵点P(m,9)在函数y=2x-1的图象上,
∴2m-1=9,
解得:m=5.
4.下表是丽丽往姥姥家打长途电话的几次收费记录:
时间(分) 1 2 3 4 5 6 7
电话费(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)如果用x表示时间,y表示电话费,上表反映了哪两个变量之间的关系?请用式子表示它们的关系.
(2)随x的变化,y的变化趋势是什么?
(3)丽丽打了5分钟电话,那么电话费需付多少元?
(4)你能帮丽丽预测一下,如果打10分钟的电话,需付多少元话费?
解:(1)电话费与时间之间的关系,y=0.6x
(2)随x的增大,y也随之增大.
(3)当x=5时,y=0.6×5=3(元)
(4)当x=10时,y=0.6×10=6(元)
四、课堂小结
今天我们学习了哪些知识?
1.函数有哪几种表示方法?它们各有什么优点?
2.如何根据函数分析变量的变化规律和变化趋势?
五、布置作业
教材P80页练习题第3题.
