福建省普通高中2022-2023学年高二6月学业水平合格性考试数学试题(含解析)
文档属性
| 名称 | 福建省普通高中2022-2023学年高二6月学业水平合格性考试数学试题(含解析) | 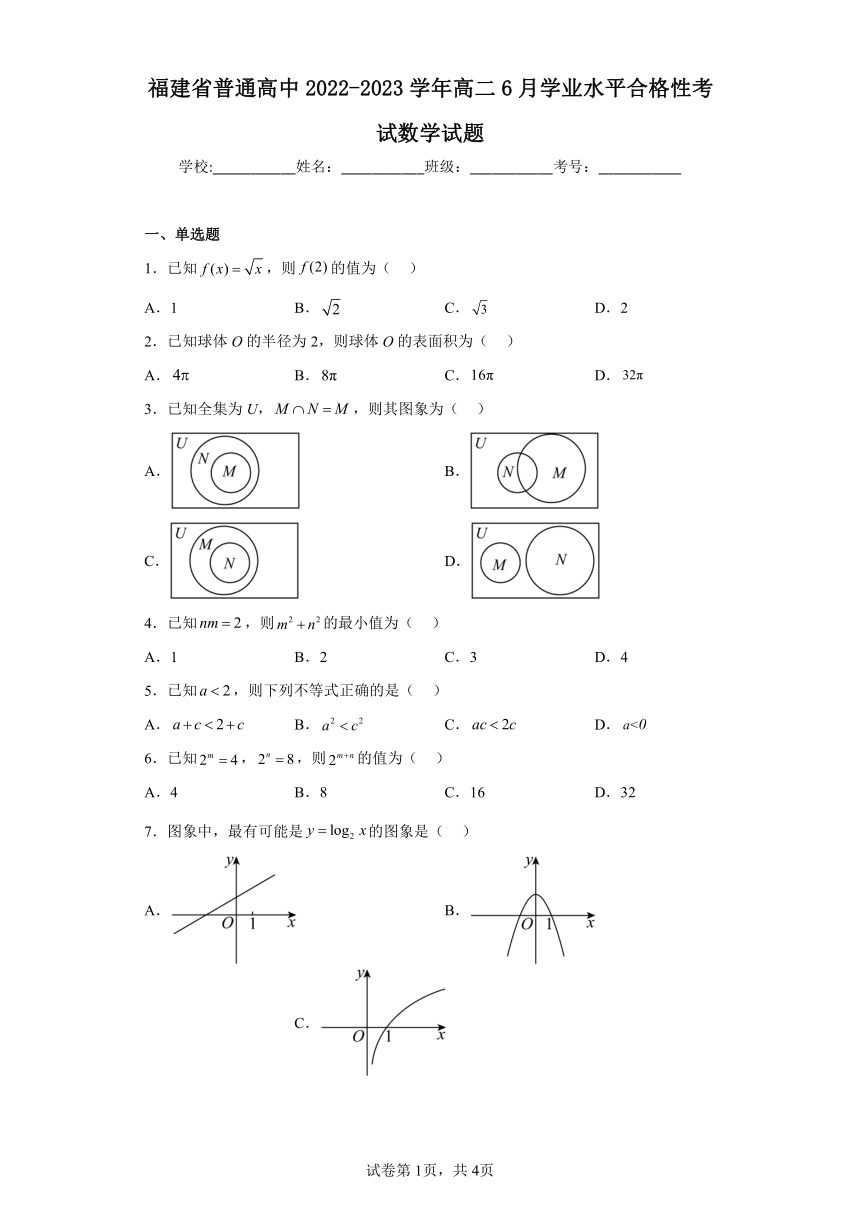 | |
| 格式 | docx | ||
| 文件大小 | 726.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 05:48:53 | ||
图片预览




文档简介
福建省普通高中2022-2023学年高二6月学业水平合格性考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,则的值为( )
A.1 B. C. D.2
2.已知球体O的半径为2,则球体O的表面积为( )
A. B. C. D.
3.已知全集为U,,则其图象为( )
A. B.
C. D.
4.已知,则的最小值为( )
A.1 B.2 C.3 D.4
5.已知,则下列不等式正确的是( )
A. B. C. D.
6.已知,,则的值为( )
A.4 B.8 C.16 D.32
7.图象中,最有可能是的图象是( )
A. B. C. D.
8.厦门中学生小助团队的几名成员考试成绩分别为73 76 81 83 85 88 91 93 95,则几人考试成绩的中位数是( )
A.76 B.81 C.85 D.91
9.求2sin15°cos15°的值( )
A. B. C. D.
10.已知,,且,则y的值为( )
A.3 B. C.4 D.
11.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则值为( )
A. B. C. D.
12.“敬骅号”列车一排共有A、B、C、D、F五个座位,其中A和F座是靠窗位,若小曾同学想要坐靠窗位,则购票时选到A或F座的概率为( )
A. B. C. D.
13.已知,则上的所有点全部向右移动个单位的函数解析式是( )
A. B.
C. D.
14.如图所示,,,M为AB的中点,则为( )
A. B.
C. D.
15.下列函数为增函数的是( )
A. B.
C. D.
16.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
17.已知,,则的周期为( )
A. B. C. D.
18.已知四棱锥底面为正方形,平面,则( )
A. B.
C.平面 D.平面
19.厦门市实行“阶梯水价”,具体收费标准如表所示
不超过12的部分 3元/
超过12不超过18的部分 6元/
超过18的部分 9元/
若小曾同学用水量为16,则应交水费( )(单位:元)
A.48 B.60 C.72 D.80
二、填空题
20.已知为虚数单位,则____.
21.已知,,若A,B相互独立,则= ____.
22.已知分别为三个内角的对边,若,,则= ____.
23.敬骅小区共有100名住户,该小区用电量千瓦时(kW·h)频率分布表如下表所示.求的户数 ____.
频率/组距 用电量
0 (0,50]
0.0024 (50,100]
0.0036 (100,150]
0.0056 (150,200]
0.0042 (200,250]
0.0030 (250,300]
0.0012 (300,350]
三、解答题
24.已知分别为三个内角的对边,.
(1)求的值;
(2)若,求b的值.
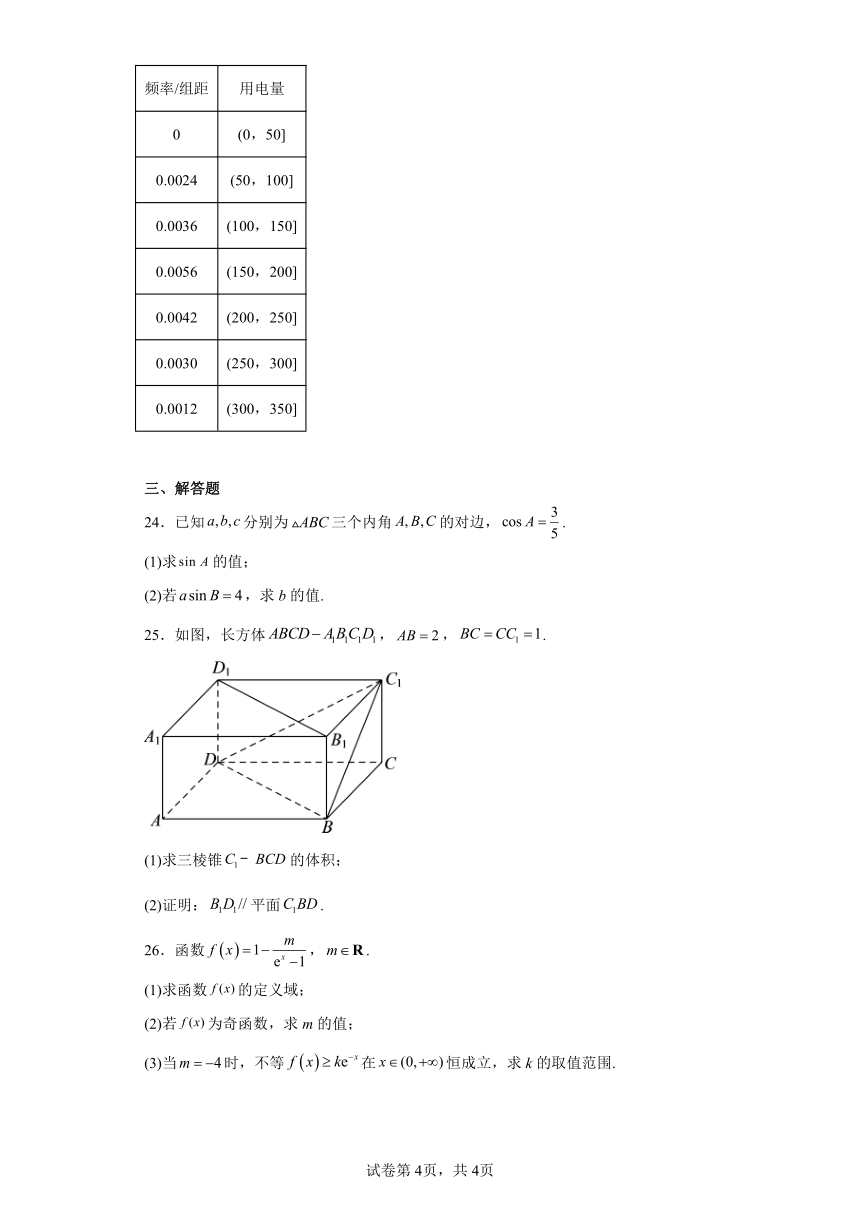
25.如图,长方体,,.
(1)求三棱锥的体积;
(2)证明:平面.
26.函数,.
(1)求函数的定义域;
(2)若为奇函数,求m的值;
(3)当时,不等在恒成立,求k的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】直接代入求解即可.
【详解】因为,则,
故选:B.
2.C
【分析】由球的表面积公式求解即可.
【详解】设球体O的半径为,所以
由球体O的表面积公式可得.
故选:C.
3.A
【分析】根据给定条件,可得,结合韦恩图的意义判断作答.
【详解】全集为U,,则有,选项BCD不符合题意,选项A符合题意.
故选:A
4.D
【分析】由基本不等式求解即可.
【详解】,当且仅当“”时取等.
故的最小值为.
故选:D.
5.A
【分析】由不等式的性质可判断A;由特值法可判断BCD.
【详解】对于A,,由不等式的性质可得,故A正确;
对于B,,取,所以,故B不正确;
对于C,,若,则,故C不正确;
对于D,,取,故D不正确.
故选:A.
6.D
【分析】根据给定条件,利用指数运算法则计算作答.
【详解】因为,,所以.
故选:D
7.C
【分析】利用对数函数的定义域,确定图象位置即可判断作答.
【详解】函数的定义域为,因此函数的图象总在y轴右侧,选项ABD不满足,C满足.
故选:C
8.C
【分析】由中位数的定义求解即可.
【详解】73,76,81,83,85,88,91,93,95的中位数为 85.
故选:C.
9.D
【分析】直接逆用正弦的二倍角公式求解.
【详解】
故选:D.
10.A
【分析】利用向量共线的坐标表示列式计算作答.
【详解】因为,,且,则,解得,
所以y的值为3.
故选:A
11.D
【分析】由三角函数的定义可得出的值.
【详解】已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,
由三角函数的定义可得.
故选:D.
12.B
【分析】根据给定条件,利用古典概率求解作答.
【详解】小曾购票的不同结果有5个,它们等可能,而小曾选到A或F座的结果有2个,
所以购票时选到A或F座的概率为.
故选:B
13.B
【分析】根据给定条件,利用函数图象变换求出函数解析式作答.
【详解】把上的所有点全部向右移动个单位的函数解析式是.
故选:B
14.B
【分析】根据给定条件,利用向量的加法列式作答.
【详解】,,M为AB的中点,
所以.
故选:B
15.A
【分析】利用基本初等函数的单调性逐项判断,可得出合适的选项.
【详解】对于A选项,函数为上的增函数;
对于B选项,函数在上不单调;
对于C选项,函数为上的减函数;
对于D选项,函数为上的减函数.
故选:A.
16.C
【分析】由充分条件和必要条件的定义求解即可.
【详解】由可得,由可得,
所以“”是“”的充要条件.
故选:C.
17.D
【分析】由余弦函数的最小正周期公式即可得出答案.
【详解】的最小正周期为:.
故选:D.
18.B
【分析】推导出,可判断A选项;利用线面垂直的性质可判断B选项;利用反证法可判断CD选项.
【详解】对于A选项,因为平面,平面,则,
因为四边形为正方形,则,
因为,、平面,所以,平面,
因为平面,则,故为锐角,A错;
对于B选项,因为平面,平面,则,B对;
对于C选项,若平面,且平面,则、平行或重合,
矛盾,假设不成立,C错;
对于D选项,若平面,则与平面无公共点,
这与平面矛盾,假设不成立,D错.
故选:B.
19.B
【分析】根据给定的数表,分段计算即可作答.
【详解】因为小曾同学用水量为16,则不超过12的部分的水费为(元),
显然没有超过18,则超过12不超过18的部分的水费为(元),
所以应交水费为(元).
故选:B
20.
【分析】利用复数的乘法化简可得结果.
【详解】.
故答案为:.
21.0.35/
【分析】根据给定条件,利用相互独立事件的概率公式计算作答.
【详解】因为,,且A,B相互独立,
所以.
故答案为:
22./
【分析】由余弦定理代入求解即可.
【详解】由余弦定理,则,
又,所以,
故答案为:.
23.21
【分析】根据频数=频率样本总量,由表求解即可.
【详解】由题,组距为50,则的户数为户,
故答案为:21.
24.(1)
(2)
【分析】(1)由同一个角的正余弦平方和为1求解即可;
(2)由正弦定理,代入原式求出b.
【详解】(1)在中,因为,所以.
(2)由正弦定理,,又,
所以.
25.(1)
(2)证明见解析
【分析】(1)利用锥体体积公式可求得三棱锥的体积;
(2)证明出,利用线面平行的判定定理可证得结论成立.
【详解】(1)解:在长方体中,平面,且,
因为,,则,,
因此,三棱锥的体积为.
(2)证明:在长方体中,且,
所以,四边形为平行四边形,则,
因为平面,平面,因此,平面.
26.(1)
(2)
(3)
【分析】(1)由具体函数的定义域可得,求解即可;
(2)由化简即可得出答案;
(3)由题意可得在恒成立,令,由基本不等式求出即可得出答案.
【详解】(1)依题意可得,解得,
所以的定义域为.
(2)若为奇函数,所以,
,所以,
所以,所以.
(3)当时,,
所以不等式在恒成立,即,
即,令,
,
因为,所以,
所以,
当且仅当取等,
所以.
故k的取值范围为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,则的值为( )
A.1 B. C. D.2
2.已知球体O的半径为2,则球体O的表面积为( )
A. B. C. D.
3.已知全集为U,,则其图象为( )
A. B.
C. D.
4.已知,则的最小值为( )
A.1 B.2 C.3 D.4
5.已知,则下列不等式正确的是( )
A. B. C. D.
6.已知,,则的值为( )
A.4 B.8 C.16 D.32
7.图象中,最有可能是的图象是( )
A. B. C. D.
8.厦门中学生小助团队的几名成员考试成绩分别为73 76 81 83 85 88 91 93 95,则几人考试成绩的中位数是( )
A.76 B.81 C.85 D.91
9.求2sin15°cos15°的值( )
A. B. C. D.
10.已知,,且,则y的值为( )
A.3 B. C.4 D.
11.已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,则值为( )
A. B. C. D.
12.“敬骅号”列车一排共有A、B、C、D、F五个座位,其中A和F座是靠窗位,若小曾同学想要坐靠窗位,则购票时选到A或F座的概率为( )
A. B. C. D.
13.已知,则上的所有点全部向右移动个单位的函数解析式是( )
A. B.
C. D.
14.如图所示,,,M为AB的中点,则为( )
A. B.
C. D.
15.下列函数为增函数的是( )
A. B.
C. D.
16.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
17.已知,,则的周期为( )
A. B. C. D.
18.已知四棱锥底面为正方形,平面,则( )
A. B.
C.平面 D.平面
19.厦门市实行“阶梯水价”,具体收费标准如表所示
不超过12的部分 3元/
超过12不超过18的部分 6元/
超过18的部分 9元/
若小曾同学用水量为16,则应交水费( )(单位:元)
A.48 B.60 C.72 D.80
二、填空题
20.已知为虚数单位,则____.
21.已知,,若A,B相互独立,则= ____.
22.已知分别为三个内角的对边,若,,则= ____.
23.敬骅小区共有100名住户,该小区用电量千瓦时(kW·h)频率分布表如下表所示.求的户数 ____.
频率/组距 用电量
0 (0,50]
0.0024 (50,100]
0.0036 (100,150]
0.0056 (150,200]
0.0042 (200,250]
0.0030 (250,300]
0.0012 (300,350]
三、解答题
24.已知分别为三个内角的对边,.
(1)求的值;
(2)若,求b的值.
25.如图,长方体,,.
(1)求三棱锥的体积;
(2)证明:平面.
26.函数,.
(1)求函数的定义域;
(2)若为奇函数,求m的值;
(3)当时,不等在恒成立,求k的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】直接代入求解即可.
【详解】因为,则,
故选:B.
2.C
【分析】由球的表面积公式求解即可.
【详解】设球体O的半径为,所以
由球体O的表面积公式可得.
故选:C.
3.A
【分析】根据给定条件,可得,结合韦恩图的意义判断作答.
【详解】全集为U,,则有,选项BCD不符合题意,选项A符合题意.
故选:A
4.D
【分析】由基本不等式求解即可.
【详解】,当且仅当“”时取等.
故的最小值为.
故选:D.
5.A
【分析】由不等式的性质可判断A;由特值法可判断BCD.
【详解】对于A,,由不等式的性质可得,故A正确;
对于B,,取,所以,故B不正确;
对于C,,若,则,故C不正确;
对于D,,取,故D不正确.
故选:A.
6.D
【分析】根据给定条件,利用指数运算法则计算作答.
【详解】因为,,所以.
故选:D
7.C
【分析】利用对数函数的定义域,确定图象位置即可判断作答.
【详解】函数的定义域为,因此函数的图象总在y轴右侧,选项ABD不满足,C满足.
故选:C
8.C
【分析】由中位数的定义求解即可.
【详解】73,76,81,83,85,88,91,93,95的中位数为 85.
故选:C.
9.D
【分析】直接逆用正弦的二倍角公式求解.
【详解】
故选:D.
10.A
【分析】利用向量共线的坐标表示列式计算作答.
【详解】因为,,且,则,解得,
所以y的值为3.
故选:A
11.D
【分析】由三角函数的定义可得出的值.
【详解】已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边经过点,
由三角函数的定义可得.
故选:D.
12.B
【分析】根据给定条件,利用古典概率求解作答.
【详解】小曾购票的不同结果有5个,它们等可能,而小曾选到A或F座的结果有2个,
所以购票时选到A或F座的概率为.
故选:B
13.B
【分析】根据给定条件,利用函数图象变换求出函数解析式作答.
【详解】把上的所有点全部向右移动个单位的函数解析式是.
故选:B
14.B
【分析】根据给定条件,利用向量的加法列式作答.
【详解】,,M为AB的中点,
所以.
故选:B
15.A
【分析】利用基本初等函数的单调性逐项判断,可得出合适的选项.
【详解】对于A选项,函数为上的增函数;
对于B选项,函数在上不单调;
对于C选项,函数为上的减函数;
对于D选项,函数为上的减函数.
故选:A.
16.C
【分析】由充分条件和必要条件的定义求解即可.
【详解】由可得,由可得,
所以“”是“”的充要条件.
故选:C.
17.D
【分析】由余弦函数的最小正周期公式即可得出答案.
【详解】的最小正周期为:.
故选:D.
18.B
【分析】推导出,可判断A选项;利用线面垂直的性质可判断B选项;利用反证法可判断CD选项.
【详解】对于A选项,因为平面,平面,则,
因为四边形为正方形,则,
因为,、平面,所以,平面,
因为平面,则,故为锐角,A错;
对于B选项,因为平面,平面,则,B对;
对于C选项,若平面,且平面,则、平行或重合,
矛盾,假设不成立,C错;
对于D选项,若平面,则与平面无公共点,
这与平面矛盾,假设不成立,D错.
故选:B.
19.B
【分析】根据给定的数表,分段计算即可作答.
【详解】因为小曾同学用水量为16,则不超过12的部分的水费为(元),
显然没有超过18,则超过12不超过18的部分的水费为(元),
所以应交水费为(元).
故选:B
20.
【分析】利用复数的乘法化简可得结果.
【详解】.
故答案为:.
21.0.35/
【分析】根据给定条件,利用相互独立事件的概率公式计算作答.
【详解】因为,,且A,B相互独立,
所以.
故答案为:
22./
【分析】由余弦定理代入求解即可.
【详解】由余弦定理,则,
又,所以,
故答案为:.
23.21
【分析】根据频数=频率样本总量,由表求解即可.
【详解】由题,组距为50,则的户数为户,
故答案为:21.
24.(1)
(2)
【分析】(1)由同一个角的正余弦平方和为1求解即可;
(2)由正弦定理,代入原式求出b.
【详解】(1)在中,因为,所以.
(2)由正弦定理,,又,
所以.
25.(1)
(2)证明见解析
【分析】(1)利用锥体体积公式可求得三棱锥的体积;
(2)证明出,利用线面平行的判定定理可证得结论成立.
【详解】(1)解:在长方体中,平面,且,
因为,,则,,
因此,三棱锥的体积为.
(2)证明:在长方体中,且,
所以,四边形为平行四边形,则,
因为平面,平面,因此,平面.
26.(1)
(2)
(3)
【分析】(1)由具体函数的定义域可得,求解即可;
(2)由化简即可得出答案;
(3)由题意可得在恒成立,令,由基本不等式求出即可得出答案.
【详解】(1)依题意可得,解得,
所以的定义域为.
(2)若为奇函数,所以,
,所以,
所以,所以.
(3)当时,,
所以不等式在恒成立,即,
即,令,
,
因为,所以,
所以,
当且仅当取等,
所以.
故k的取值范围为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
