4.5 利用三角形全等测距离 同步练习(含答案) 北师大版数学七年级下册
文档属性
| 名称 | 4.5 利用三角形全等测距离 同步练习(含答案) 北师大版数学七年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 18:32:31 | ||
图片预览


文档简介
4.5 利用三角形全等测距离 同步练习
一、单选题
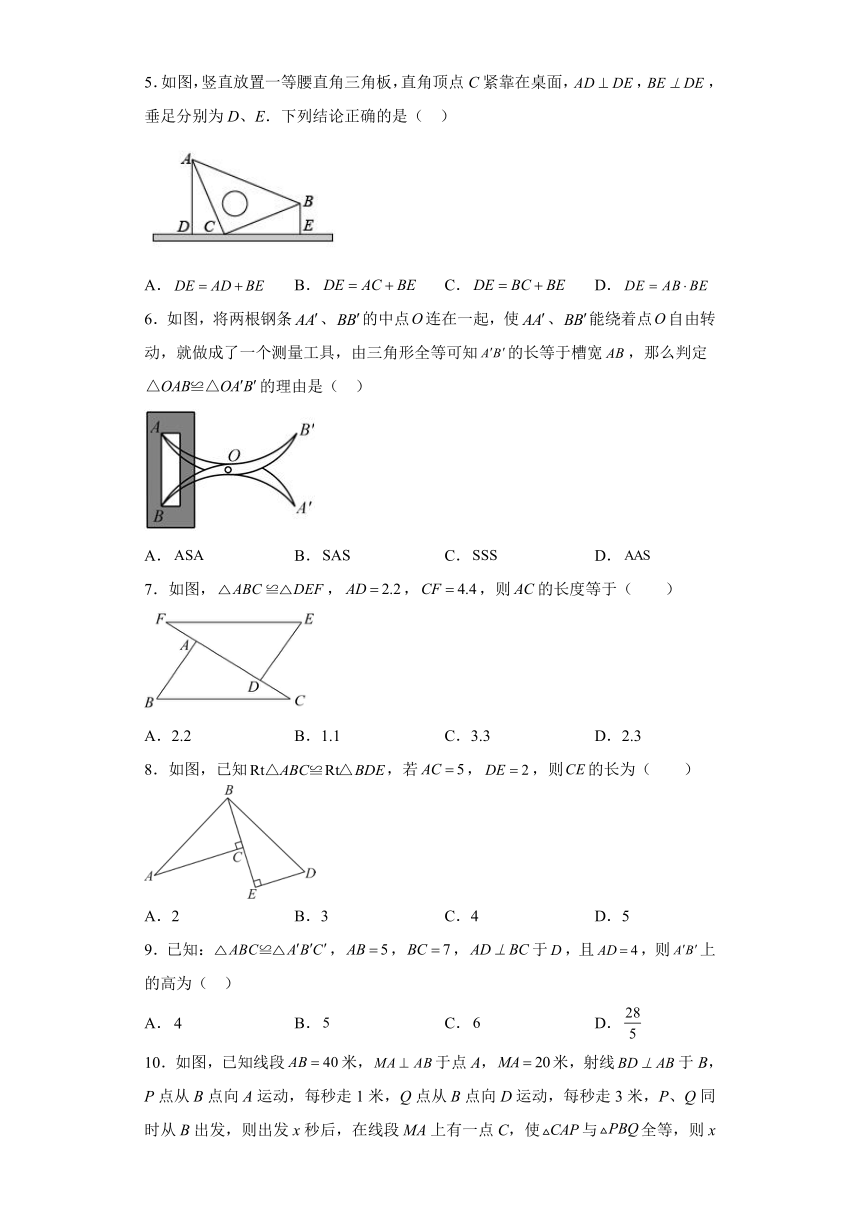
1.如图,小明利用全等三角形的知识测量池塘两端M、N的距离,若,则只需测出其长度的线段是( )
A. B. C. D.
2.如图,,,,则的长是( )
A.5 B.4 C.3 D.2
3.下面各图中所给数据的三角形,甲、乙、丙三个三角形和左侧全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
4.如图,图中的两个三角形是全等三角形,其中一些角和边的大小如图所示,那么x的值是( )
A. B. C. D.
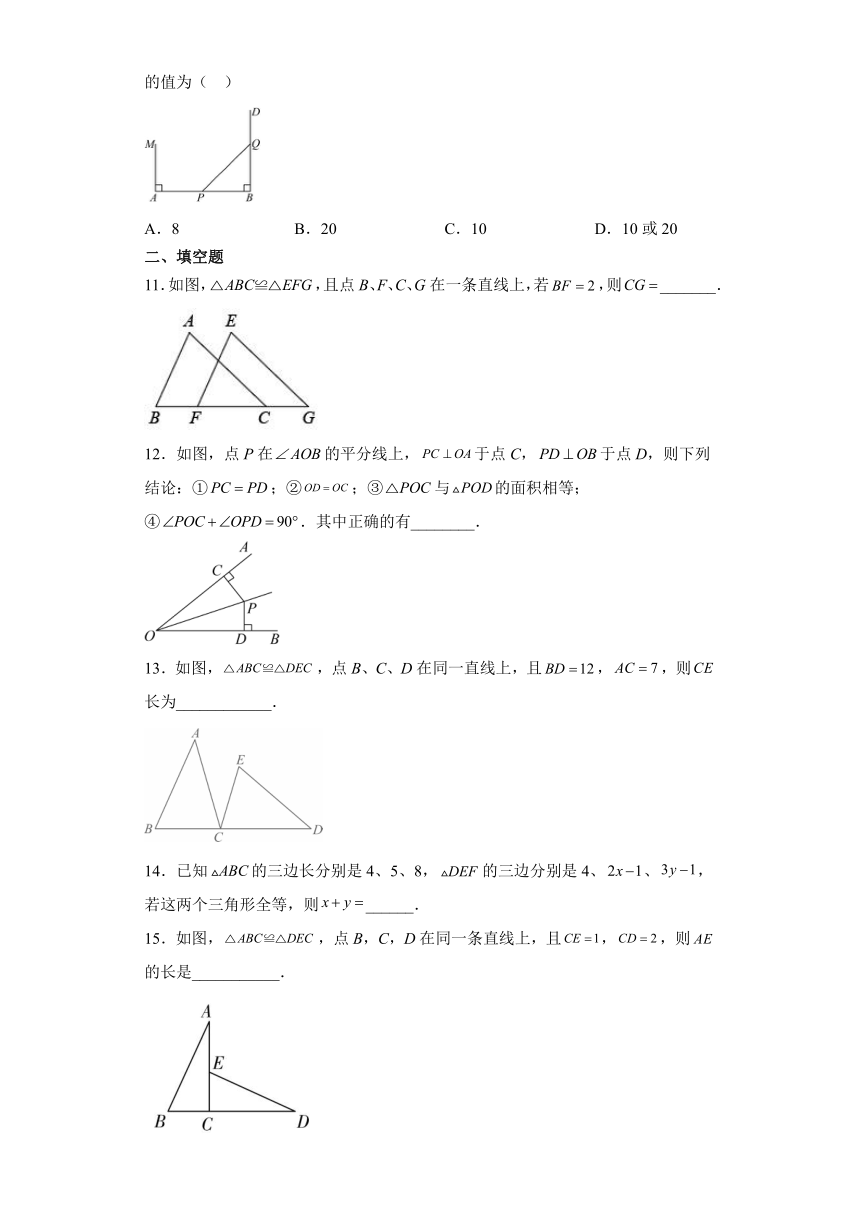
5.如图,竖直放置一等腰直角三角板,直角顶点C紧靠在桌面,,,垂足分别为D、E.下列结论正确的是( )
A. B. C. D.
6.如图,将两根钢条、的中点连在一起,使、能绕着点自由转动,就做成了一个测量工具,由三角形全等可知的长等于槽宽,那么判定的理由是( )
A. B. C. D.
7.如图,,,,则的长度等于( )
A.2.2 B.1.1 C.3.3 D.2.3
8.如图,已知,若,,则的长为( )
A.2 B.3 C.4 D.5
9.已知:,,,于,且,则上的高为( )
A. B. C. D.
10.如图,已知线段米,于点A,米,射线于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使与全等,则x的值为( )
A.8 B.20 C.10 D.10或20
二、填空题
11.如图,,且点B、F、C、G在一条直线上,若,则_______.
12.如图,点P在的平分线上,于点C,于点D,则下列结论:①;②;③与的面积相等;④.其中正确的有________.
13.如图,,点B、C、D在同一直线上,且,,则长为____________.
14.已知的三边长分别是4、5、8,的三边分别是4、、,若这两个三角形全等,则______.
15.如图,,点B,C,D在同一条直线上,且,,则的长是___________.
16.如图,已知,于点,于点,与相交于点,连接,则图中共有______对全等三角形.
17.中,,边上的中线,则边的取值范围是__.
18.如图,,,动点从点出发(不含点)以2个单位长度/秒的速度沿射线运动,点为射线上一动点,且始终保持,当点运动__________秒时,与以点,,为顶点的三角形全等.
三、解答题
19.如图,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走有一树C,继续前行到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得的长为6米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
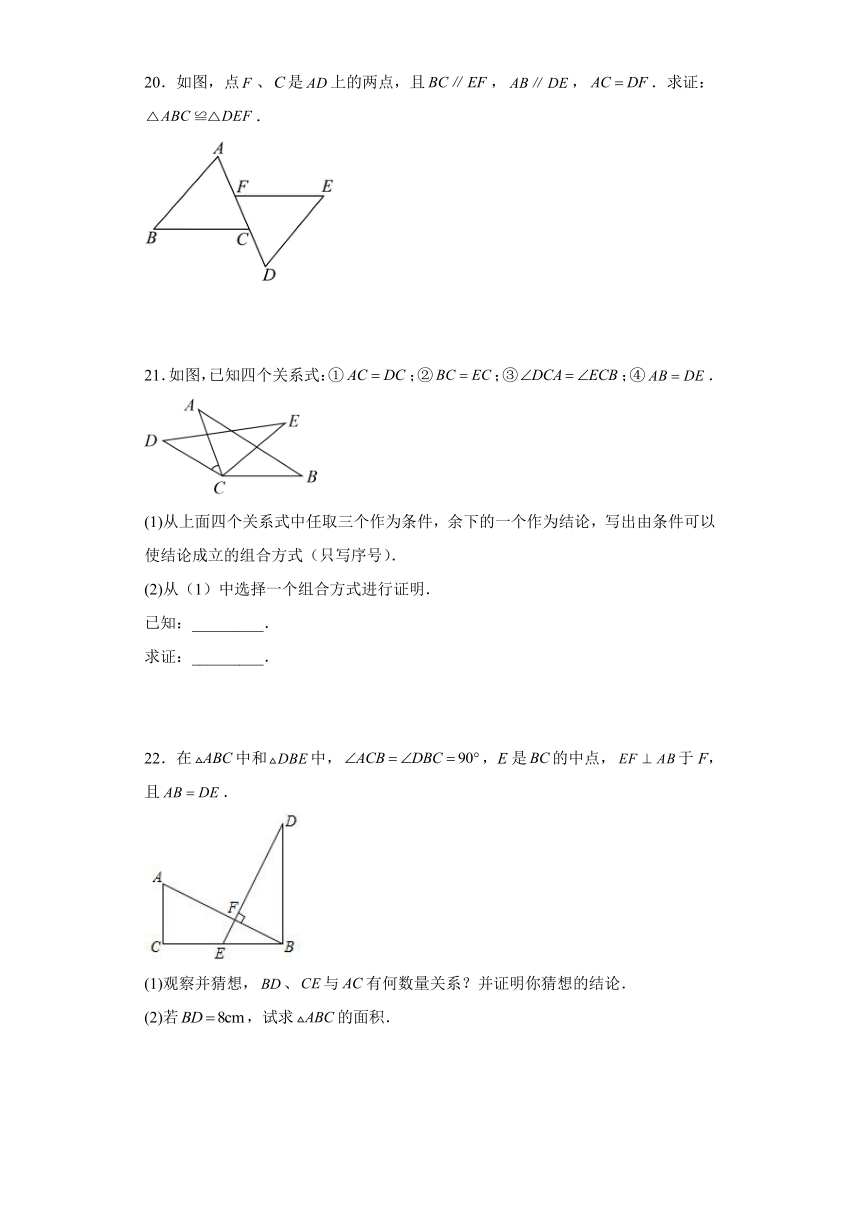
20.如图,点、是上的两点,且,,.求证:.
21.如图,已知四个关系式:①;②;③;④.
(1)从上面四个关系式中任取三个作为条件,余下的一个作为结论,写出由条件可以使结论成立的组合方式(只写序号).
(2)从(1)中选择一个组合方式进行证明.
已知:_________.
求证:_________.
22.在中和中,,E是的中点,于F,且.
(1)观察并猜想,、与有何数量关系?并证明你猜想的结论.
(2)若,试求的面积.
23.如图,在中,,,.点P从点A出发,沿折线以每秒2个单位长度的速度向终点B运动,点Q从点B出发沿折线以每秒6个单位长度的速度向终点A运动,两点同时出发.分别过两点作于E,于F.设点P的运动时间为t(秒).
(1)当两点相遇时,求t的值.
(2)在整个运动过程中,求的长(用含t的代数式表示).
(3)当与△QFC全等时,直接写出所有满足条件的的长.
参考答案:
1.B
2.C
3.B
4.C
5.A
6.B
7.C
8.B
9.D
10.C
11.2
12.①②③④
13.5
14.6或
15.1
16.5
17.
18.1或3或4
19.【详解】(1)由数学兴趣小组的做法可知,,
故河宽为6米
(2)由题意知,米
又∵光沿直线传播
∴
又∵在和中
∴
∴.
即他们的做法是正确的.
20.【详解】解:∵,
∴,
∵,
∴,
在和中
,
.
21.【详解】(1)解:当①②③为条件,④为结论时:
∵,
∴,即,
∵,,
∴,
∴,
当①②④为条件,③为结论时:
∵,,,
∴,
∴,
∴,
∴.
∴使结论成立的组合方式有:①②③为条件,④为结论;①②④为条件,③为结论;
(2)解:已知:,,,
求证:.
证明:∵,
∴,即,
∵,,
∴,
∴.
22.【详解】(1)解:,
证明:∵,
∴,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
∴.
(2)解:∵,
∴,
∵E为中点,
∴cm,即,
.
23.【详解】(1)解:由题意得,
解得(秒),
当、两点相遇时,的值为秒;
(2)由题意可知,
则的长为;
(3)当在上,在上时,
,
,
于,于.
,,
,
,
,
,解得,
;
当在上,在上时,即、重合时,则,
由题意得,,
解得,
,
当在上,在上时,即、重合时,则,
综上,当与全等时,满足条件的的长为10或5或12.
一、单选题
1.如图,小明利用全等三角形的知识测量池塘两端M、N的距离,若,则只需测出其长度的线段是( )
A. B. C. D.
2.如图,,,,则的长是( )
A.5 B.4 C.3 D.2
3.下面各图中所给数据的三角形,甲、乙、丙三个三角形和左侧全等的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
4.如图,图中的两个三角形是全等三角形,其中一些角和边的大小如图所示,那么x的值是( )
A. B. C. D.
5.如图,竖直放置一等腰直角三角板,直角顶点C紧靠在桌面,,,垂足分别为D、E.下列结论正确的是( )
A. B. C. D.
6.如图,将两根钢条、的中点连在一起,使、能绕着点自由转动,就做成了一个测量工具,由三角形全等可知的长等于槽宽,那么判定的理由是( )
A. B. C. D.
7.如图,,,,则的长度等于( )
A.2.2 B.1.1 C.3.3 D.2.3
8.如图,已知,若,,则的长为( )
A.2 B.3 C.4 D.5
9.已知:,,,于,且,则上的高为( )
A. B. C. D.
10.如图,已知线段米,于点A,米,射线于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使与全等,则x的值为( )
A.8 B.20 C.10 D.10或20
二、填空题
11.如图,,且点B、F、C、G在一条直线上,若,则_______.
12.如图,点P在的平分线上,于点C,于点D,则下列结论:①;②;③与的面积相等;④.其中正确的有________.
13.如图,,点B、C、D在同一直线上,且,,则长为____________.
14.已知的三边长分别是4、5、8,的三边分别是4、、,若这两个三角形全等,则______.
15.如图,,点B,C,D在同一条直线上,且,,则的长是___________.
16.如图,已知,于点,于点,与相交于点,连接,则图中共有______对全等三角形.
17.中,,边上的中线,则边的取值范围是__.
18.如图,,,动点从点出发(不含点)以2个单位长度/秒的速度沿射线运动,点为射线上一动点,且始终保持,当点运动__________秒时,与以点,,为顶点的三角形全等.
三、解答题
19.如图,某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走有一树C,继续前行到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得的长为6米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
20.如图,点、是上的两点,且,,.求证:.
21.如图,已知四个关系式:①;②;③;④.
(1)从上面四个关系式中任取三个作为条件,余下的一个作为结论,写出由条件可以使结论成立的组合方式(只写序号).
(2)从(1)中选择一个组合方式进行证明.
已知:_________.
求证:_________.
22.在中和中,,E是的中点,于F,且.
(1)观察并猜想,、与有何数量关系?并证明你猜想的结论.
(2)若,试求的面积.
23.如图,在中,,,.点P从点A出发,沿折线以每秒2个单位长度的速度向终点B运动,点Q从点B出发沿折线以每秒6个单位长度的速度向终点A运动,两点同时出发.分别过两点作于E,于F.设点P的运动时间为t(秒).
(1)当两点相遇时,求t的值.
(2)在整个运动过程中,求的长(用含t的代数式表示).
(3)当与△QFC全等时,直接写出所有满足条件的的长.
参考答案:
1.B
2.C
3.B
4.C
5.A
6.B
7.C
8.B
9.D
10.C
11.2
12.①②③④
13.5
14.6或
15.1
16.5
17.
18.1或3或4
19.【详解】(1)由数学兴趣小组的做法可知,,
故河宽为6米
(2)由题意知,米
又∵光沿直线传播
∴
又∵在和中
∴
∴.
即他们的做法是正确的.
20.【详解】解:∵,
∴,
∵,
∴,
在和中
,
.
21.【详解】(1)解:当①②③为条件,④为结论时:
∵,
∴,即,
∵,,
∴,
∴,
当①②④为条件,③为结论时:
∵,,,
∴,
∴,
∴,
∴.
∴使结论成立的组合方式有:①②③为条件,④为结论;①②④为条件,③为结论;
(2)解:已知:,,,
求证:.
证明:∵,
∴,即,
∵,,
∴,
∴.
22.【详解】(1)解:,
证明:∵,
∴,
∵,
∴,,
∴,
在和中,
,
∴,
∴,
∴.
(2)解:∵,
∴,
∵E为中点,
∴cm,即,
.
23.【详解】(1)解:由题意得,
解得(秒),
当、两点相遇时,的值为秒;
(2)由题意可知,
则的长为;
(3)当在上,在上时,
,
,
于,于.
,,
,
,
,
,解得,
;
当在上,在上时,即、重合时,则,
由题意得,,
解得,
,
当在上,在上时,即、重合时,则,
综上,当与全等时,满足条件的的长为10或5或12.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
