4.3探索三角形全等的条件 同步练习(二) 北师大版数学七年级下册(含答案)
文档属性
| 名称 | 4.3探索三角形全等的条件 同步练习(二) 北师大版数学七年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 00:00:00 | ||
图片预览



文档简介
4.3探索三角形全等的条件 同步练习二
一、单选题
1.如图,已知AC平分,于E,,则下列结论①;②;③;④.其中,正确结论的个数( )
A.1个 B.2个 C.3个 D.4个
2.如图所示,是线段上一点,分别以,为边在同侧作等边和等边,交于,交于,则图中可通过旋转而得到的全等三角形的对数为( )对.
A.1 B.2
C.3 D.4
3.如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是( )
A.2<AD<3 B.3<AD<5 C.1<AD<4 D.2<AD<8
4.在中,,,是边上的中线,则的取值范围是( )
A. B. C. D.
5.下列说法中,正确的是( )
A.周长相等的两个直角三角形全等 B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等 D.周长相等的两个等边三角形全等
6.如图,△ABC是一个什么三角形?( )请说明理由.
A.等腰三角形; B.等边三角形
C.直角三角形; D.等腰直角三角形
7.根据下列已知条件,能唯一画出的是( ).
A. B.
C. D.
8.如图,,,要使,应添加的条件是( )
A. B. C. D.
9.如图所示,,,点、、在一条直线上,,,,则( )
A. B. C. D.
10.如图,CAAB,垂足为点A,AB=24cm,AC=12cm,射线BMAB,垂足为点B,一动点E从A点出发以3cm/s沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过 ( ) 秒时,△DEB与△BCA全等.(注:点E与A不重合)( )
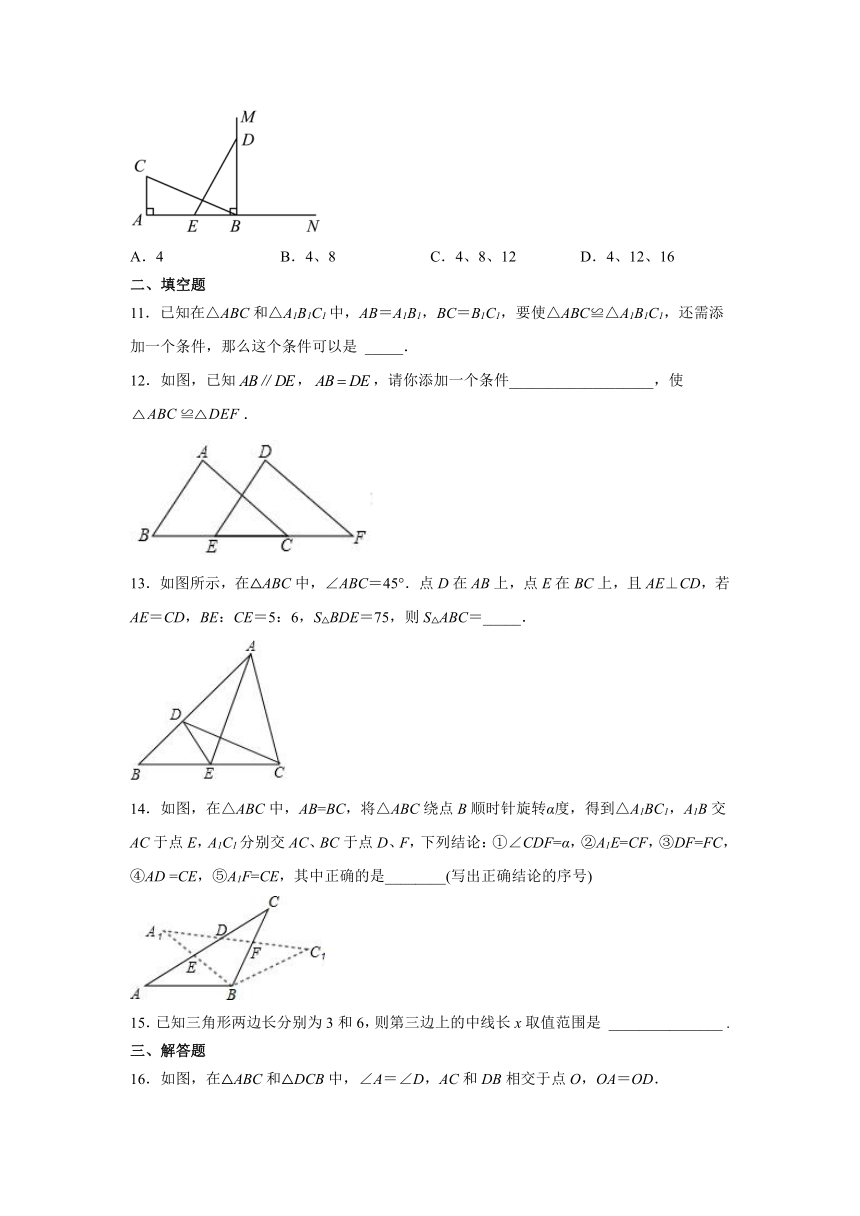
A.4 B.4、8 C.4、8、12 D.4、12、16
二、填空题
11.已知在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,要使△ABC≌△A1B1C1,还需添加一个条件,那么这个条件可以是 _____.
12.如图,已知,,请你添加一个条件___________________,使.
13.如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.
14.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD =CE,⑤A1F=CE,其中正确的是________(写出正确结论的序号)
15.已知三角形两边长分别为3和6,则第三边上的中线长x取值范围是 _______________ .
三、解答题
16.如图,在△ABC和△DCB中,∠A=∠D,AC和DB相交于点O,OA=OD.
(1)AB=DC;
(2)△ABC≌△DCB.
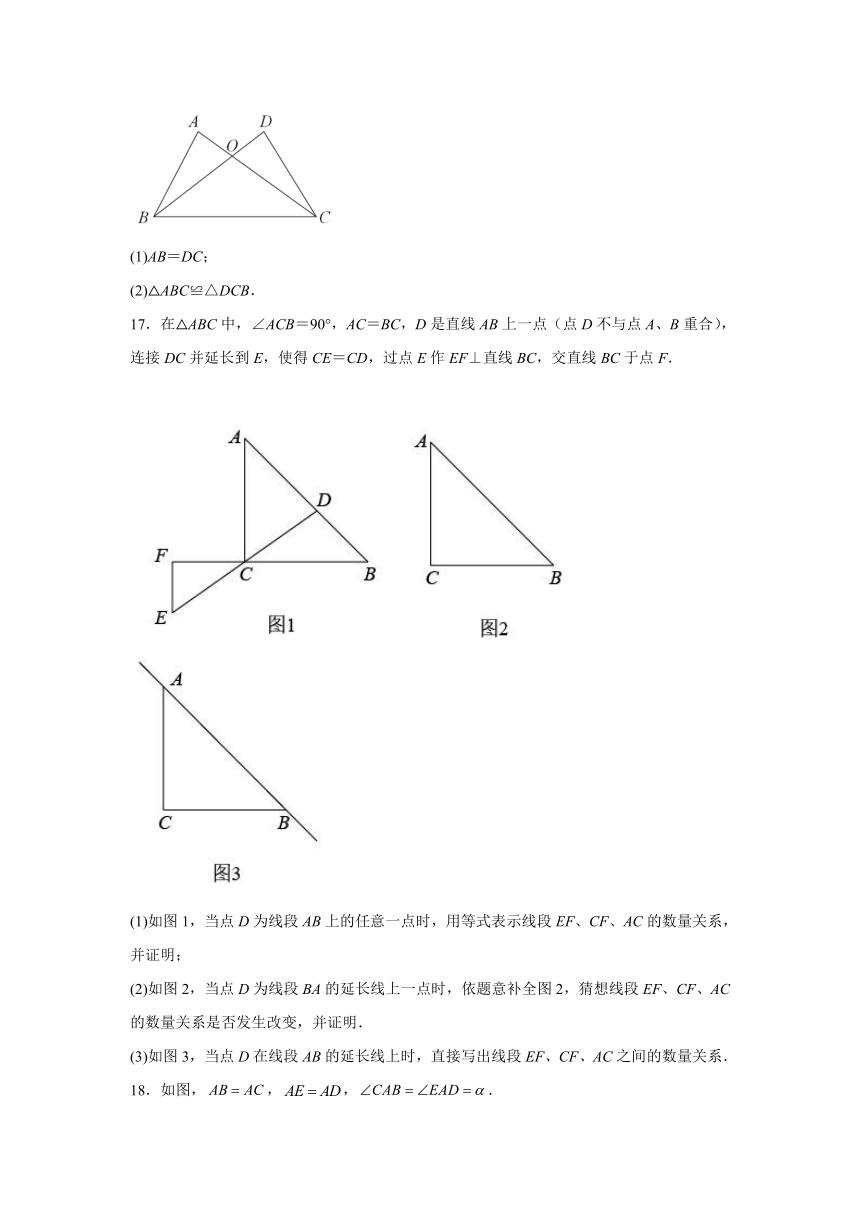
17.在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.
(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;
(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明.
(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.
18.如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
19.问题背景:课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=4,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,则得到△ADC≌△EDB,小明证明△BED≌△CAD用到的判定定理是: (用字母表示);
问题解决:小明发现:解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.请写出小明解决问题的完整过程;
拓展应用:以△ABC的边AB,AC为边向外作△ABE和△ACD,AB=AE,AC=AD,∠BAE=∠CAD=90°,M是BC中点,连接AM,DE.当AM=3时,求DE的长.
20.在四边形中,,,,、分别是,上的点,且,在探究图1中线段,,之间的数量关系过程中.
(1)你尝试添加了怎样的辅助线?成功了吗?(真实大胆作答即可得分)
(2)小亮同学认为:延长到点,使,连接,先证明,再证明,即可得出,,之间的数量关系是 .
(3)如图3,在四边形中,,,、分别是,上的点,且,上述结论是否仍然成立?并证明;
(4)如图4,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以70海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达,处,且两舰艇之间的夹角为,试求此时两舰艇之间的距离.
参考答案
1--10DCCBD DCCAD
11.AC=A1C1或∠B=∠B1
12.(答案不唯一)
13.440.
14.①②⑤
15.
16.(1)证明:在△ABO与△DCO中,
,
∴△ABO≌△DCO(ASA)
∴AB=DC;
(2)证明:∵△ABO≌△DCO,
∴OB=OC,
∵OA=OD,
∴OB+OD=OC+OA,
∴BD=AC,
在△ABC与△DCB中,
,
∴△ABC≌△DCB(SAS).
17.(1)结论:AC=EF+FC,
理由如下:过D作DH⊥CB于H,
∴∠DHC=∠DHB= 90°
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
,
∴△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠ACB=90°,AC=BC,
∴∠B=45°,
∵∠DHB=90°,
∴∠B=∠HDB=45°
∴DH=HB=EF,
∵BC=CB+HB
∴AC=FC+EF;
(2)依题意补全图形,结论:AC=EF-CF,
理由如下:
过D作DH⊥CB交BC的延长线于H,
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
,
∴△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠DHB=90°,
∴∠B=∠HDB=45°
∴DH=HB=EF,
∵BC=HB-CH
∴AC=EF-CF.
(3)AC=CF-EF.
如图3,过D作DH⊥CB交CB的延长线于H,
同理可证△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠DHB=90°,
∴∠B=∠HDB=45°,
∴DH=HB=EF,
∵BC=CH-BH,
∴AC=CF-EF.
18.(1)∵∠CAB=∠EAD
∴∠CAB+∠BAE=∠EAD+∠BAE,
∴ ∠CAE=∠BAD,
∵AB=AC,AE=AD
在△AEC和△ADB中
∴ △AEC≌△ADB(SAS)
(2)CE=BD且CE⊥BD,证明如下:
将直线CE与AB的交点记为点O,
由(1)可知△AEC≌△ADB,
∴ CE=BD, ∠ACE=∠ABD,
∵∠BOF=∠AOC,∠=90°,
∴ ∠BFO=∠CAB=∠=90°,
∴ CE⊥BD.
(3)过A分别做AM⊥CE,AN⊥BD
由(1)知△AEC≌△ADB,
∴两个三角形面积相等
故AM·CE=AN·BD
∴AM=AN
∴AF平分∠DFC
由(2)可知∠BFC=∠BAC=
∴∠DFC=180°-
∴∠CFA=∠DFC=
19.问题背景:如图1,延长AD到点E,使DE=AD,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故答案为:SAS;
问题解决:如图1,延长AD到点E,使DE=AD,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC≌△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC,
在△ABE中,AB﹣BE<AE<AB+BE,
∵AB=4,AC=3,
∴4﹣3<AE<4+3,即1<AE<7,
∵DE=AD,
∴AD=AE,
∴<AD<;
拓展应用:如图2,延长AM到N,使得MN=AM,连接BN,
由问题背景知,△BMN≌△CMA(SAS),
∴BN=AC,∠CAM=∠BNM,
∴AC//BN,
∵AC=AD,
∴BN=AD,
∵AC//BN,
∴∠BAC+∠ABN=180°,
∵∠BAE=∠CAD=90°,
∴∠BAC+∠EAD=180°,
∴∠ABN=∠EAD,
在△ABN和△EAD中,
,
∴△ABN≌△EAD(SAS),
∴AN=DE,
∵MN=AM,
∴DE=AN=2AM,
∵AM=3,
∴DE=6.
20.(1)在上方作,使,连接,
在和中,
,
,
,
,,
,
,
在和中,
,
,
,
,即,
添加辅助线:在上方作,使,连接,成功了;
(2)延长到点,使,连接,
,
,
在和中,
,
,
,,
,,
,
,
在和中,
,
,
,
,即,
故答案为:;
(3)结论仍然成立,
证明:延长到,使,连接,
,,
,
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
;
(4)如图4,连接,延长、交于点,
,
,
,
,
,
符合(3)中的条件,
结论成立,
即(海里),
答:此时两舰艇之间的距离是195海里.
一、单选题
1.如图,已知AC平分,于E,,则下列结论①;②;③;④.其中,正确结论的个数( )
A.1个 B.2个 C.3个 D.4个
2.如图所示,是线段上一点,分别以,为边在同侧作等边和等边,交于,交于,则图中可通过旋转而得到的全等三角形的对数为( )对.
A.1 B.2
C.3 D.4
3.如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是( )
A.2<AD<3 B.3<AD<5 C.1<AD<4 D.2<AD<8
4.在中,,,是边上的中线,则的取值范围是( )
A. B. C. D.
5.下列说法中,正确的是( )
A.周长相等的两个直角三角形全等 B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等 D.周长相等的两个等边三角形全等
6.如图,△ABC是一个什么三角形?( )请说明理由.
A.等腰三角形; B.等边三角形
C.直角三角形; D.等腰直角三角形
7.根据下列已知条件,能唯一画出的是( ).
A. B.
C. D.
8.如图,,,要使,应添加的条件是( )
A. B. C. D.
9.如图所示,,,点、、在一条直线上,,,,则( )
A. B. C. D.
10.如图,CAAB,垂足为点A,AB=24cm,AC=12cm,射线BMAB,垂足为点B,一动点E从A点出发以3cm/s沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过 ( ) 秒时,△DEB与△BCA全等.(注:点E与A不重合)( )
A.4 B.4、8 C.4、8、12 D.4、12、16
二、填空题
11.已知在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,要使△ABC≌△A1B1C1,还需添加一个条件,那么这个条件可以是 _____.
12.如图,已知,,请你添加一个条件___________________,使.
13.如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.
14.如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④AD =CE,⑤A1F=CE,其中正确的是________(写出正确结论的序号)
15.已知三角形两边长分别为3和6,则第三边上的中线长x取值范围是 _______________ .
三、解答题
16.如图,在△ABC和△DCB中,∠A=∠D,AC和DB相交于点O,OA=OD.
(1)AB=DC;
(2)△ABC≌△DCB.
17.在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.
(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;
(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明.
(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.
18.如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
19.问题背景:课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=4,AC=3,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,则得到△ADC≌△EDB,小明证明△BED≌△CAD用到的判定定理是: (用字母表示);
问题解决:小明发现:解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.请写出小明解决问题的完整过程;
拓展应用:以△ABC的边AB,AC为边向外作△ABE和△ACD,AB=AE,AC=AD,∠BAE=∠CAD=90°,M是BC中点,连接AM,DE.当AM=3时,求DE的长.
20.在四边形中,,,,、分别是,上的点,且,在探究图1中线段,,之间的数量关系过程中.
(1)你尝试添加了怎样的辅助线?成功了吗?(真实大胆作答即可得分)
(2)小亮同学认为:延长到点,使,连接,先证明,再证明,即可得出,,之间的数量关系是 .
(3)如图3,在四边形中,,,、分别是,上的点,且,上述结论是否仍然成立?并证明;
(4)如图4,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以70海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达,处,且两舰艇之间的夹角为,试求此时两舰艇之间的距离.
参考答案
1--10DCCBD DCCAD
11.AC=A1C1或∠B=∠B1
12.(答案不唯一)
13.440.
14.①②⑤
15.
16.(1)证明:在△ABO与△DCO中,
,
∴△ABO≌△DCO(ASA)
∴AB=DC;
(2)证明:∵△ABO≌△DCO,
∴OB=OC,
∵OA=OD,
∴OB+OD=OC+OA,
∴BD=AC,
在△ABC与△DCB中,
,
∴△ABC≌△DCB(SAS).
17.(1)结论:AC=EF+FC,
理由如下:过D作DH⊥CB于H,
∴∠DHC=∠DHB= 90°
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
,
∴△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠ACB=90°,AC=BC,
∴∠B=45°,
∵∠DHB=90°,
∴∠B=∠HDB=45°
∴DH=HB=EF,
∵BC=CB+HB
∴AC=FC+EF;
(2)依题意补全图形,结论:AC=EF-CF,
理由如下:
过D作DH⊥CB交BC的延长线于H,
∵EF⊥CF,
∴∠EFC=∠DHC=90°,
在△FEC和△HDC中,
,
∴△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠DHB=90°,
∴∠B=∠HDB=45°
∴DH=HB=EF,
∵BC=HB-CH
∴AC=EF-CF.
(3)AC=CF-EF.
如图3,过D作DH⊥CB交CB的延长线于H,
同理可证△FEC≌△HDC(AAS),
∴CH=FC,DH=EF,
∵∠DHB=90°,
∴∠B=∠HDB=45°,
∴DH=HB=EF,
∵BC=CH-BH,
∴AC=CF-EF.
18.(1)∵∠CAB=∠EAD
∴∠CAB+∠BAE=∠EAD+∠BAE,
∴ ∠CAE=∠BAD,
∵AB=AC,AE=AD
在△AEC和△ADB中
∴ △AEC≌△ADB(SAS)
(2)CE=BD且CE⊥BD,证明如下:
将直线CE与AB的交点记为点O,
由(1)可知△AEC≌△ADB,
∴ CE=BD, ∠ACE=∠ABD,
∵∠BOF=∠AOC,∠=90°,
∴ ∠BFO=∠CAB=∠=90°,
∴ CE⊥BD.
(3)过A分别做AM⊥CE,AN⊥BD
由(1)知△AEC≌△ADB,
∴两个三角形面积相等
故AM·CE=AN·BD
∴AM=AN
∴AF平分∠DFC
由(2)可知∠BFC=∠BAC=
∴∠DFC=180°-
∴∠CFA=∠DFC=
19.问题背景:如图1,延长AD到点E,使DE=AD,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故答案为:SAS;
问题解决:如图1,延长AD到点E,使DE=AD,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC≌△EDB中,
,
∴△ADC≌△EDB(SAS),
∴BE=AC,
在△ABE中,AB﹣BE<AE<AB+BE,
∵AB=4,AC=3,
∴4﹣3<AE<4+3,即1<AE<7,
∵DE=AD,
∴AD=AE,
∴<AD<;
拓展应用:如图2,延长AM到N,使得MN=AM,连接BN,
由问题背景知,△BMN≌△CMA(SAS),
∴BN=AC,∠CAM=∠BNM,
∴AC//BN,
∵AC=AD,
∴BN=AD,
∵AC//BN,
∴∠BAC+∠ABN=180°,
∵∠BAE=∠CAD=90°,
∴∠BAC+∠EAD=180°,
∴∠ABN=∠EAD,
在△ABN和△EAD中,
,
∴△ABN≌△EAD(SAS),
∴AN=DE,
∵MN=AM,
∴DE=AN=2AM,
∵AM=3,
∴DE=6.
20.(1)在上方作,使,连接,
在和中,
,
,
,
,,
,
,
在和中,
,
,
,
,即,
添加辅助线:在上方作,使,连接,成功了;
(2)延长到点,使,连接,
,
,
在和中,
,
,
,,
,,
,
,
在和中,
,
,
,
,即,
故答案为:;
(3)结论仍然成立,
证明:延长到,使,连接,
,,
,
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
;
(4)如图4,连接,延长、交于点,
,
,
,
,
,
符合(3)中的条件,
结论成立,
即(海里),
答:此时两舰艇之间的距离是195海里.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
