10.5角平分线 同步练习题 鲁教版(五四制)七年级数学下册(含答案)
文档属性
| 名称 | 10.5角平分线 同步练习题 鲁教版(五四制)七年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 246.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 22:50:47 | ||
图片预览



文档简介
2022-2023学年鲁教版(五四学制)七年级数学下册《10.5角平分线》同步练习题(附答案)
一.选择题
1.如图,直线AB,CD相交于点O,PE⊥CD于E,PF⊥AB于F,若PE=PF,∠AOC=50°,则∠AOP的度数为( )
A.65° B.60° C.40° D.30°
2.如图,在CD上求一点P,使它到OA、OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与∠CDB的平分线的交点
C.OB与∠DCA的平分线的交点
D.CD与∠AOB的平分线的交点
3.△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=( )
A.110° B.120° C.130° D.140°
4.如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
A.120° B.90° C.75° D.60°
5.如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
6.如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
①OC平分∠ACB;②∠AOC=90°+∠ABC;③OD⊥BC;④OA=OB=OC;⑤∠AOE+∠DCO=90°其中正确的有( )个.
A.2 B.3 C.4 D.5
7.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.① B.② C.①② D.①②③
8.如图,BI,CI分别是∠ABC和∠ACB的平分线,DE过I点且DE∥BC,则下列结论错误的是( )
A.I到三边的距离相等 B.∠BIC=90°+∠A
C.DE=BD+CE D.AI=AE
9.如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )
A.70° B.120° C.125° D.130°
10.如图,在△ABC中,∠ACB=90°,角平分线BE、AD相交于I,连接CI并延长交AB于点F,则下列结论中错误的是( )
A.点I在∠ABC的平分线上 B.点F在∠AIB的平分线上
C.∠ACI=45° D.∠CAD+∠ABE+∠BCF=90°
11.如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P,下列结论:
①PC平分∠ACF;
②∠ABC+∠APC=180°;
③若点M、N分别为点P在BE、BF上的正投影,则AM+CN=AC;
④∠BAC=2∠BPC.
其中正确的是( )
A.只有①②③ B.只有①③④ C.只有②③④ D.只有①③
二.填空题
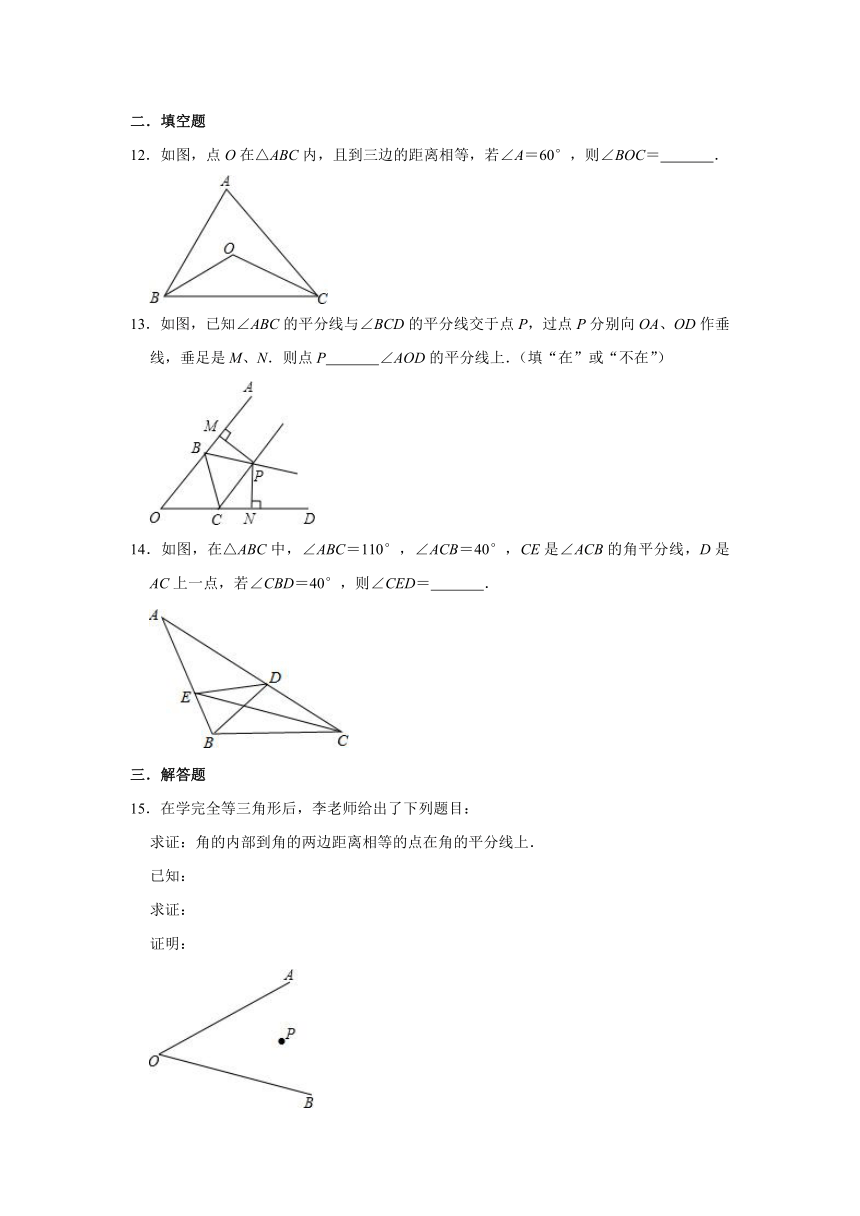
12.如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC= .
13.如图,已知∠ABC的平分线与∠BCD的平分线交于点P,过点P分别向OA、OD作垂线,垂足是M、N.则点P ∠AOD的平分线上.(填“在”或“不在”)
14.如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED= .
三.解答题
15.在学完全等三角形后,李老师给出了下列题目:
求证:角的内部到角的两边距离相等的点在角的平分线上.
已知:
求证:
证明:
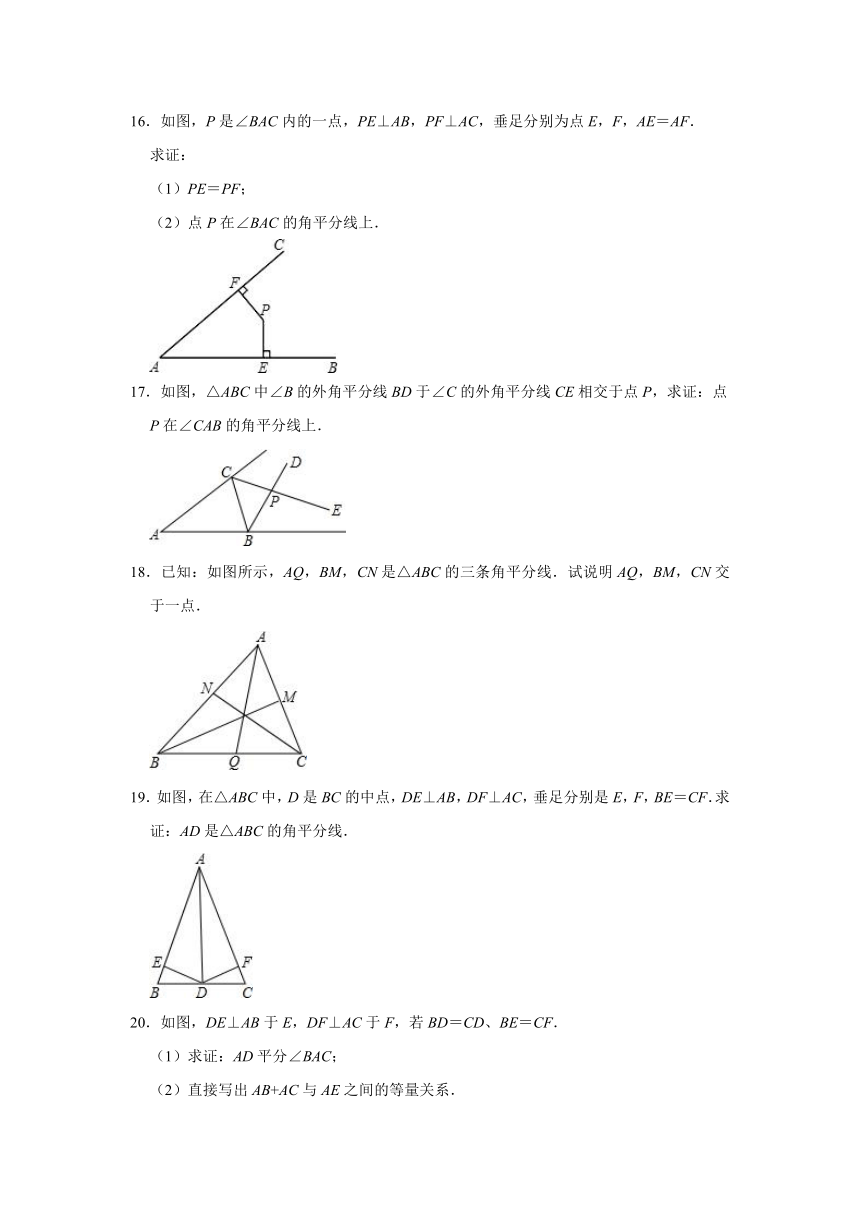
16.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.
17.如图,△ABC中∠B的外角平分线BD于∠C的外角平分线CE相交于点P,求证:点P在∠CAB的角平分线上.
18.已知:如图所示,AQ,BM,CN是△ABC的三条角平分线.试说明AQ,BM,CN交于一点.
19.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.
20.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
21.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
(1)求证:AM平分∠BAD;
(2)试说明线段DM与AM有怎样的位置关系?
(3)线段CD、AB、AD间有怎样的关系?直接写出结果.
参考答案
一.选择题
1.解:∵∠AOC=50°,
∴∠AOD=180°﹣50°=130°,
∵PE⊥CD于E,PF⊥AB于F,PE=PF,
∴OP平分∠AOD,
∴∠AOP=∠AOD=×130°=65°.
故选:A.
2.解:∵点P到OA、OB的距离相等,
∴点P在∠AOB平分线上,
∴点P是CD与∠AOB平分线的交点,
故选:D.
3.解:∵O到三角形三边距离相等,
∴O是内心,
即三条角平分线交点,AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠OBC+∠OCB=70°,
∴∠BOC=180°﹣70°=110°.
故选:A.
4.解:∵点P到AB、BC、CD距离都相等,
∴BP、CP分别是∠ABC和∠BCD的平分线,
∴∠CBP=∠ABC,∠BCP=∠BCD,
∴∠CBP+∠BCP=(∠ABC+∠BCD),
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBP+∠BCP=×180°=90°,
∴∠P=180°﹣(∠CBP+∠BCP)=180°﹣90°=90°.
故选:B.
5.解:∵AD⊥OB,BC⊥OA,
∴∠ACP=∠BDP,∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP
∴CP=DP
∴OP是角AOB的平分线,
∴∠1=∠2.
故选:A.
6.解:∵AD和BE是△ABC的角平分线且交于点O,
∴点O是△ABC的角平分线的交点,
∴OC平分∠ACB,故①正确;
由角平分线的定义,∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣∠ABC)=90°﹣∠ABC,
在△OAC中,∠AOC=180°﹣(90°﹣∠ABC)=90°+∠ABC,故②正确;
只有AB=AC时,OD⊥BC,故③错误;
△ABC是等边三角形时,OA=OB=OC,故④错误;
由三角形的外角性质得,∠AOE=∠OAB+∠OBA=(∠BAC+∠ABC),
∠AOE+∠DCO=(∠BAC+∠ABC)+∠ACB=90°,故⑤正确;
综上所述,正确的结论有①②⑤共3个.
故选:B.
7.解:∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90°,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF(第一个正确)
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,∠BDF=∠CDE,
∴△BDF≌△CDE(第二个正确)
∴DF=DE,
连接AD
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上(第三个正确)
故选:D.
8.解:A、过点I作IM⊥BC于M,IN⊥AC于N,IK⊥AB于K,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴IK=IM,IM=IN,
∴IK=IM=IN,
∴I到三边的距离相等,
故本选项正确;
B、∵∠ABC+∠ACB=180°﹣∠A,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A,
故本选项正确;
C、∵DE∥BC,
∴∠DIB=∠IBC,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴∠DBI=∠IBC,
∴∠DBI=∠DIB,
∴DI=DB,
同理:EI=EC,
∴DE=DI+IE=BD+CE,
故本选项正确;
D、∵∠AIE不一定等于∠AEI,
∴AI不一定等于AE,
故本选项错误.
故选:D.
9.解:∵O到三边AB、BC、CA的距离OF=OD=OE,
∴点O是三角形三条角平分线的交点,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°﹣70°=110°,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×110°=55°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:C.
10.解:A、∵在△ABC中,角平分线BE、AD相交于I,
∴点I在∠ABC的平分线上,故本选项正确;
B、过I点分别作AB、BC、AC的垂线,垂足分别为M、N、P,
∵在△ABC中,角平分线BE、AD相交于I,
∴IM=IN,IM=IP,
∴IN=IP,
∴CF平分∠ACB,∠ACF=∠BCF.
∵∠AIF=∠ACI+∠CAI,∠BIF=∠BCI+∠CBI,
∠ACI=∠BCI,∠CAI≠∠CBI,
∴∠AIF≠∠BIF,
∴点F不在∠AIB的平分线上,故本选项错误;
C、∵∠ACB=90°,CI平分∠ACB,
∴∠ACI=∠ACB=45°,故本选项正确;
D、∵BE、AD、CF是△ABC的角平分线,
∴∠CAD=∠BAC,∠ABE=∠ABC,∠BCF=∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠CAD+∠ABE+∠BCF=(∠BAC+∠ABC+∠ACB)=90°,故本选项正确.
故选:B.
11.解:如图,过点P作PM⊥AB,PN⊥BC,PD⊥AC,垂足分别为M、N、D,
①∵PB平分∠ABC,PA平分∠EAC,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
故本小题正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
很明显∠MPN≠∠APC,
∴∠ABC+∠APC=180°错误,
故本小题错误;
③在Rt△APM与Rt△APD中,,
∴Rt△APM≌Rt△APD(HL),
∴AD=AM,
同理可得Rt△CPD≌Rt△CPN,
∴CD=CN,
∴AM+CN=AD+CD=AC,
故本小题正确;
④∵PB平分∠ABC,PC平分∠ACF,
∴∠ACF=∠ABC+∠BAC,∠PCN=∠ACF=∠BPC+∠ABC,
∴∠BAC=2∠BPC,
故本小题正确.
综上所述,①③④正确.
故选:B.
二.填空题
12.解:∵点O在△ABC内,且到三边的距离相等,
∴点O是三个角的平分线的交点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)=(180°﹣60°)=60°,
在△BCO中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°.
故答案为:120°.
13.解:过P作PH⊥BC于点H,
∵BP、CP分别平分∠ABC和∠BCD,且PM⊥OA,PN⊥OD,
∴PM=PH=PN,
∴P在∠AOD的平分线上,
故答案为:在.
14.解:∠A=180°﹣∠ACB﹣∠ABC=180°﹣110°﹣40°=30°,
∵作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N、M、H,∠ABC=110°,∠CBD=40°,
∴∠ABD=70°,
∴∠ABC的外角是∠ABM=180°﹣110°=70°;
∴BE是∠DBM的角平分线,
∴EM=EN,
∵CE是∠ACB的平分线,EM⊥CB,EH⊥AC,
∴EM=EH,
∴EH=EN,
∴DE是∠ADB的平分线,
∵∠ADB=180°﹣∠A﹣∠ABD=180°﹣30°﹣70°=80°,
∴∠ADE=∠ADB=40°=∠ACB,
∴DE∥CB,
∴∠CED=∠ECB=20°
故答案为:20°.
三.解答题
15.已知:PE=PF,PE⊥OA于E,PF⊥OB于F,
求证:点P在∠AOB的平分线上.
证明:在Rt△POE和Rt△POF中,
,
∴Rt△POE≌△RtPOF,
∴∠EOP=∠FOP,
∴点P在∠AOB的平分线上.
16.证明:(1)如图,连接AP并延长,
∵PE⊥AB,PF⊥AC
∴∠AEP=∠AFP=90°
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.
17.证明:作PF⊥AB于F,PG⊥BC于G,PH⊥AC于H,
∵∠B的外角平分线BD与∠C的外角平分线CE相交于点P,
∴PF=PG,PH=PG,
∴PF=PH,又PF⊥AB,PH⊥AC,
∴点P在∠CAB的角平分线上.
18.证明:设BM,CN交于点P,过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足分别为:D,E,F,
∵BM平分∠ABC,CN平分∠ACB,
∴PD=PE,PE=PF,
∴PD=PF,
∴AP平分∠BAC,
即AQ,BM,CN交于一点P.
19.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△CDF是直角三角形.
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴∠ADE=∠ADF,
∴AD是角平分线.
20.(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDF均为直角三角形,
∵
∴△BDE≌△CDF(HL).
∴DE=DF,
∵DE⊥AB于E,DF⊥AC于F,
∴AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF.
在△AED与△AFD中,
∵,
∴△AED≌△AFD(ASA).
∴AE=AF.
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
21.(1)证明:作ME⊥AD于E,
∵MC⊥DC,ME⊥DA,MD平分∠ADC,
∴ME=MC,
∵M为BC中点,
∴MB=MC,
又∵ME=MC,
∴ME=MB,
又∵ME⊥AD,MB⊥AB,
∴AM平分∠DAB.
(2)解:DM⊥AM,
理由是:∵DM平分∠CDA,AM平分∠DAB,
∴∠1=∠2,∠3=∠4,
∵DC∥AB,
∴∠CDA+∠BAD=180°,
∴∠1+∠3=90°,
∴∠DMA=180°﹣(∠1+∠3)=90°,
即DM⊥AM.
(3)解:CD+AB=AD,
理由是:∵ME⊥AD,MC⊥CD,
∴∠C=∠DEM=90°,
在Rt△DCM和Rt△DEM中
∴Rt△DCM≌Rt△DEM(HL),
∴CD=DE,
同理AE=AB,
∵AE+DE=AD,
∴CD+AB=AD.
一.选择题
1.如图,直线AB,CD相交于点O,PE⊥CD于E,PF⊥AB于F,若PE=PF,∠AOC=50°,则∠AOP的度数为( )
A.65° B.60° C.40° D.30°
2.如图,在CD上求一点P,使它到OA、OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与∠CDB的平分线的交点
C.OB与∠DCA的平分线的交点
D.CD与∠AOB的平分线的交点
3.△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等;∠A=40°,则∠BOC=( )
A.110° B.120° C.130° D.140°
4.如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
A.120° B.90° C.75° D.60°
5.如图所示,AD⊥OB,BC⊥OA,垂足分别为D、C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
6.如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
①OC平分∠ACB;②∠AOC=90°+∠ABC;③OD⊥BC;④OA=OB=OC;⑤∠AOE+∠DCO=90°其中正确的有( )个.
A.2 B.3 C.4 D.5
7.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
A.① B.② C.①② D.①②③
8.如图,BI,CI分别是∠ABC和∠ACB的平分线,DE过I点且DE∥BC,则下列结论错误的是( )
A.I到三边的距离相等 B.∠BIC=90°+∠A
C.DE=BD+CE D.AI=AE
9.如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数为( )
A.70° B.120° C.125° D.130°
10.如图,在△ABC中,∠ACB=90°,角平分线BE、AD相交于I,连接CI并延长交AB于点F,则下列结论中错误的是( )
A.点I在∠ABC的平分线上 B.点F在∠AIB的平分线上
C.∠ACI=45° D.∠CAD+∠ABE+∠BCF=90°
11.如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P,下列结论:
①PC平分∠ACF;
②∠ABC+∠APC=180°;
③若点M、N分别为点P在BE、BF上的正投影,则AM+CN=AC;
④∠BAC=2∠BPC.
其中正确的是( )
A.只有①②③ B.只有①③④ C.只有②③④ D.只有①③
二.填空题
12.如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC= .
13.如图,已知∠ABC的平分线与∠BCD的平分线交于点P,过点P分别向OA、OD作垂线,垂足是M、N.则点P ∠AOD的平分线上.(填“在”或“不在”)
14.如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED= .
三.解答题
15.在学完全等三角形后,李老师给出了下列题目:
求证:角的内部到角的两边距离相等的点在角的平分线上.
已知:
求证:
证明:
16.如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.
17.如图,△ABC中∠B的外角平分线BD于∠C的外角平分线CE相交于点P,求证:点P在∠CAB的角平分线上.
18.已知:如图所示,AQ,BM,CN是△ABC的三条角平分线.试说明AQ,BM,CN交于一点.
19.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.求证:AD是△ABC的角平分线.
20.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
21.已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
(1)求证:AM平分∠BAD;
(2)试说明线段DM与AM有怎样的位置关系?
(3)线段CD、AB、AD间有怎样的关系?直接写出结果.
参考答案
一.选择题
1.解:∵∠AOC=50°,
∴∠AOD=180°﹣50°=130°,
∵PE⊥CD于E,PF⊥AB于F,PE=PF,
∴OP平分∠AOD,
∴∠AOP=∠AOD=×130°=65°.
故选:A.
2.解:∵点P到OA、OB的距离相等,
∴点P在∠AOB平分线上,
∴点P是CD与∠AOB平分线的交点,
故选:D.
3.解:∵O到三角形三边距离相等,
∴O是内心,
即三条角平分线交点,AO,BO,CO都是角平分线,
∴∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,
∴∠ABC+∠ACB=180°﹣40°=140°,
∴∠OBC+∠OCB=70°,
∴∠BOC=180°﹣70°=110°.
故选:A.
4.解:∵点P到AB、BC、CD距离都相等,
∴BP、CP分别是∠ABC和∠BCD的平分线,
∴∠CBP=∠ABC,∠BCP=∠BCD,
∴∠CBP+∠BCP=(∠ABC+∠BCD),
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠CBP+∠BCP=×180°=90°,
∴∠P=180°﹣(∠CBP+∠BCP)=180°﹣90°=90°.
故选:B.
5.解:∵AD⊥OB,BC⊥OA,
∴∠ACP=∠BDP,∠APC=∠BPD,PA=PB,
∴△ACP≌△BDP
∴CP=DP
∴OP是角AOB的平分线,
∴∠1=∠2.
故选:A.
6.解:∵AD和BE是△ABC的角平分线且交于点O,
∴点O是△ABC的角平分线的交点,
∴OC平分∠ACB,故①正确;
由角平分线的定义,∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣∠ABC)=90°﹣∠ABC,
在△OAC中,∠AOC=180°﹣(90°﹣∠ABC)=90°+∠ABC,故②正确;
只有AB=AC时,OD⊥BC,故③错误;
△ABC是等边三角形时,OA=OB=OC,故④错误;
由三角形的外角性质得,∠AOE=∠OAB+∠OBA=(∠BAC+∠ABC),
∠AOE+∠DCO=(∠BAC+∠ABC)+∠ACB=90°,故⑤正确;
综上所述,正确的结论有①②⑤共3个.
故选:B.
7.解:∵BE⊥AC于E,CF⊥AB于F
∴∠AEB=∠AFC=90°,
∵AB=AC,∠A=∠A,
∴△ABE≌△ACF(第一个正确)
∴AE=AF,
∴BF=CE,
∵BE⊥AC于E,CF⊥AB于F,∠BDF=∠CDE,
∴△BDF≌△CDE(第二个正确)
∴DF=DE,
连接AD
∵AE=AF,DE=DF,AD=AD,
∴△AED≌△AFD,
∴∠FAD=∠EAD,
即点D在∠BAC的平分线上(第三个正确)
故选:D.
8.解:A、过点I作IM⊥BC于M,IN⊥AC于N,IK⊥AB于K,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴IK=IM,IM=IN,
∴IK=IM=IN,
∴I到三边的距离相等,
故本选项正确;
B、∵∠ABC+∠ACB=180°﹣∠A,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A,
故本选项正确;
C、∵DE∥BC,
∴∠DIB=∠IBC,
∵BI,CI分别是∠ABC和∠ACB的平分线,
∴∠DBI=∠IBC,
∴∠DBI=∠DIB,
∴DI=DB,
同理:EI=EC,
∴DE=DI+IE=BD+CE,
故本选项正确;
D、∵∠AIE不一定等于∠AEI,
∴AI不一定等于AE,
故本选项错误.
故选:D.
9.解:∵O到三边AB、BC、CA的距离OF=OD=OE,
∴点O是三角形三条角平分线的交点,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°﹣70°=110°,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×110°=55°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:C.
10.解:A、∵在△ABC中,角平分线BE、AD相交于I,
∴点I在∠ABC的平分线上,故本选项正确;
B、过I点分别作AB、BC、AC的垂线,垂足分别为M、N、P,
∵在△ABC中,角平分线BE、AD相交于I,
∴IM=IN,IM=IP,
∴IN=IP,
∴CF平分∠ACB,∠ACF=∠BCF.
∵∠AIF=∠ACI+∠CAI,∠BIF=∠BCI+∠CBI,
∠ACI=∠BCI,∠CAI≠∠CBI,
∴∠AIF≠∠BIF,
∴点F不在∠AIB的平分线上,故本选项错误;
C、∵∠ACB=90°,CI平分∠ACB,
∴∠ACI=∠ACB=45°,故本选项正确;
D、∵BE、AD、CF是△ABC的角平分线,
∴∠CAD=∠BAC,∠ABE=∠ABC,∠BCF=∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠CAD+∠ABE+∠BCF=(∠BAC+∠ABC+∠ACB)=90°,故本选项正确.
故选:B.
11.解:如图,过点P作PM⊥AB,PN⊥BC,PD⊥AC,垂足分别为M、N、D,
①∵PB平分∠ABC,PA平分∠EAC,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
故本小题正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
很明显∠MPN≠∠APC,
∴∠ABC+∠APC=180°错误,
故本小题错误;
③在Rt△APM与Rt△APD中,,
∴Rt△APM≌Rt△APD(HL),
∴AD=AM,
同理可得Rt△CPD≌Rt△CPN,
∴CD=CN,
∴AM+CN=AD+CD=AC,
故本小题正确;
④∵PB平分∠ABC,PC平分∠ACF,
∴∠ACF=∠ABC+∠BAC,∠PCN=∠ACF=∠BPC+∠ABC,
∴∠BAC=2∠BPC,
故本小题正确.
综上所述,①③④正确.
故选:B.
二.填空题
12.解:∵点O在△ABC内,且到三边的距离相等,
∴点O是三个角的平分线的交点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣∠A)=(180°﹣60°)=60°,
在△BCO中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°.
故答案为:120°.
13.解:过P作PH⊥BC于点H,
∵BP、CP分别平分∠ABC和∠BCD,且PM⊥OA,PN⊥OD,
∴PM=PH=PN,
∴P在∠AOD的平分线上,
故答案为:在.
14.解:∠A=180°﹣∠ACB﹣∠ABC=180°﹣110°﹣40°=30°,
∵作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N、M、H,∠ABC=110°,∠CBD=40°,
∴∠ABD=70°,
∴∠ABC的外角是∠ABM=180°﹣110°=70°;
∴BE是∠DBM的角平分线,
∴EM=EN,
∵CE是∠ACB的平分线,EM⊥CB,EH⊥AC,
∴EM=EH,
∴EH=EN,
∴DE是∠ADB的平分线,
∵∠ADB=180°﹣∠A﹣∠ABD=180°﹣30°﹣70°=80°,
∴∠ADE=∠ADB=40°=∠ACB,
∴DE∥CB,
∴∠CED=∠ECB=20°
故答案为:20°.
三.解答题
15.已知:PE=PF,PE⊥OA于E,PF⊥OB于F,
求证:点P在∠AOB的平分线上.
证明:在Rt△POE和Rt△POF中,
,
∴Rt△POE≌△RtPOF,
∴∠EOP=∠FOP,
∴点P在∠AOB的平分线上.
16.证明:(1)如图,连接AP并延长,
∵PE⊥AB,PF⊥AC
∴∠AEP=∠AFP=90°
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.
17.证明:作PF⊥AB于F,PG⊥BC于G,PH⊥AC于H,
∵∠B的外角平分线BD与∠C的外角平分线CE相交于点P,
∴PF=PG,PH=PG,
∴PF=PH,又PF⊥AB,PH⊥AC,
∴点P在∠CAB的角平分线上.
18.证明:设BM,CN交于点P,过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足分别为:D,E,F,
∵BM平分∠ABC,CN平分∠ACB,
∴PD=PE,PE=PF,
∴PD=PF,
∴AP平分∠BAC,
即AQ,BM,CN交于一点P.
19.证明:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△CDF是直角三角形.
,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴∠ADE=∠ADF,
∴AD是角平分线.
20.(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDF均为直角三角形,
∵
∴△BDE≌△CDF(HL).
∴DE=DF,
∵DE⊥AB于E,DF⊥AC于F,
∴AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF.
在△AED与△AFD中,
∵,
∴△AED≌△AFD(ASA).
∴AE=AF.
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
21.(1)证明:作ME⊥AD于E,
∵MC⊥DC,ME⊥DA,MD平分∠ADC,
∴ME=MC,
∵M为BC中点,
∴MB=MC,
又∵ME=MC,
∴ME=MB,
又∵ME⊥AD,MB⊥AB,
∴AM平分∠DAB.
(2)解:DM⊥AM,
理由是:∵DM平分∠CDA,AM平分∠DAB,
∴∠1=∠2,∠3=∠4,
∵DC∥AB,
∴∠CDA+∠BAD=180°,
∴∠1+∠3=90°,
∴∠DMA=180°﹣(∠1+∠3)=90°,
即DM⊥AM.
(3)解:CD+AB=AD,
理由是:∵ME⊥AD,MC⊥CD,
∴∠C=∠DEM=90°,
在Rt△DCM和Rt△DEM中
∴Rt△DCM≌Rt△DEM(HL),
∴CD=DE,
同理AE=AB,
∵AE+DE=AD,
∴CD+AB=AD.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
