9.8相似三角形的性质(1)学案 (表格式 无答案)2022-2023学年八年级下册数学
文档属性
| 名称 | 9.8相似三角形的性质(1)学案 (表格式 无答案)2022-2023学年八年级下册数学 | 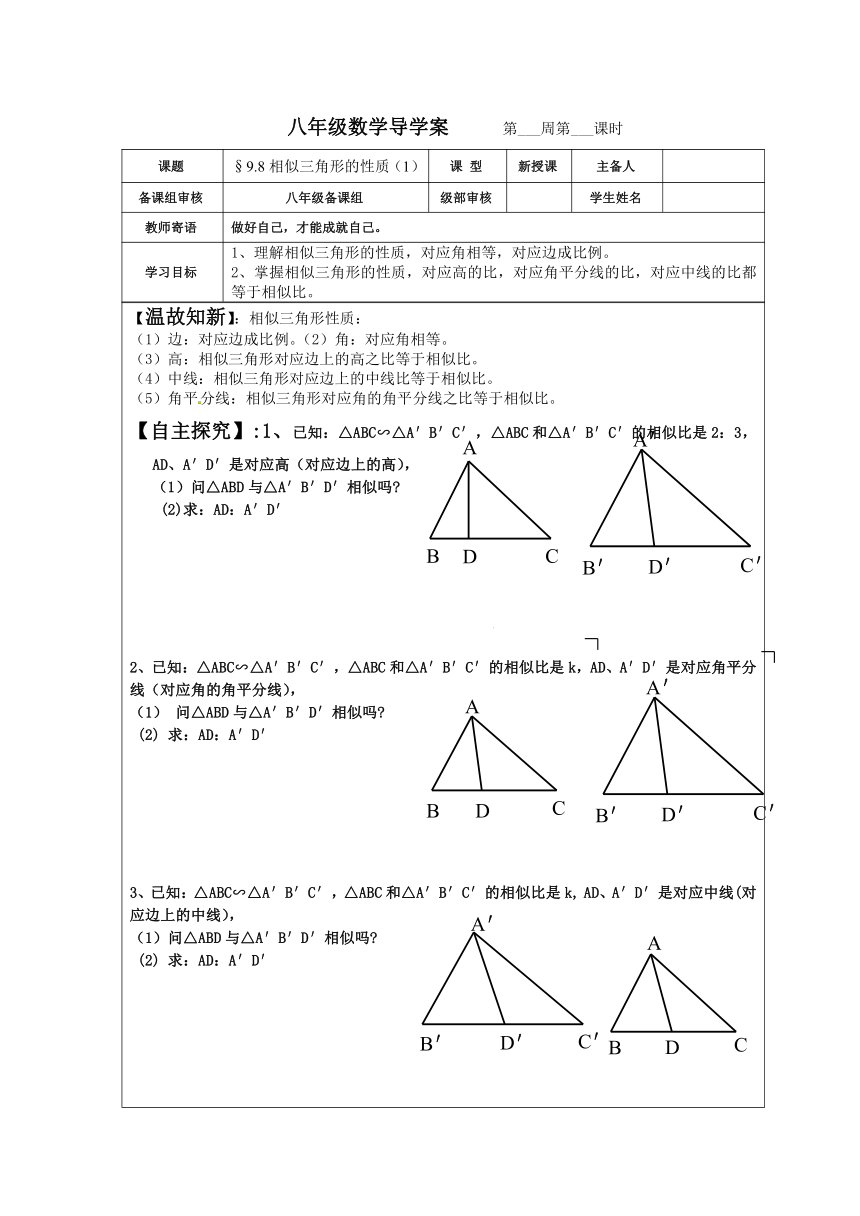 | |
| 格式 | doc | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 23:33:00 | ||
图片预览

文档简介
八年级数学导学案 第___周第___课时
课题 §9.8相似三角形的性质(1) 课 型 新授课 主备人
备课组审核 八年级备课组 级部审核 学生姓名
教师寄语 做好自己,才能成就自己。
学习目标 1、理解相似三角形的性质,对应角相等,对应边成比例。2、掌握相似三角形的性质,对应高的比,对应角平分线的比,对应中线的比都等于相似比。
【温故知新】:相似三角形性质:(1)边:对应边成比例。(2)角:对应角相等。(3)高:相似三角形对应边上的高之比等于相似比。(4)中线:相似三角形对应边上的中线比等于相似比。(5)角平分线:相似三角形对应角的角平分线之比等于相似比。【自主探究】:1、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是2:3,AD、A′D′是对应高(对应边上的高),(1)问△ABD与△A′B′D′相似吗 (2)求:AD:A′D′ 2、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是k,AD、A′D′是对应角平分线(对应角的角平分线),(1) 问△ABD与△A′B′D′相似吗 (2) 求:AD:A′D′ 3、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是k, AD、A′D′是对应中线(对应边上的中线),(1)问△ABD与△A′B′D′相似吗 (2) 求:AD:A′D′【拓展应用】1、 △ABC与△A'B'C'的相似比1:3,若BC=5cm,则B'C'=_____ 。
2、如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是__ ,对应边上的中线的比是______ 。 3、△ABC与△A'B'C'的相似比3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_____ 。4、如图所示,在△ABC中,边BC=60cm,高AD=40cm,正方形PQRS的一边PQ在BC上,另两个顶点S,R分别在AB,AC上,SR与AD相交于点E.(1) △ASR与 △ABC相似吗 为什么 (2)求正方形PQRS的边长?【课堂检测】:1、△ABC∽△A`B`C`,AD和A`D`分别是BC和B`C`边上的高,AE和A`E`分别是BC边和B`C`边上的中线,AD:A`D`=3:5,则AE:A`E`=_______,△ A`B`C 和△ABC的相似比是_________.2、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,(1)若点P到CD的距离为3m。求P到AB的距离?(2)若PE⊥CD于D交AB于F,EF=1m,求PF
自我评价专栏 自主学习: 合作与交流: 书写: 综合:
A′
C′
D′
B′
B
C
D
A
A′
C′
D′
B′
C
D
A
B
A′
C′
D′
B′
C
D
A
B
B
A
D
R
S
C
P
Q
E
D
E
F
C
A
B
P
课题 §9.8相似三角形的性质(1) 课 型 新授课 主备人
备课组审核 八年级备课组 级部审核 学生姓名
教师寄语 做好自己,才能成就自己。
学习目标 1、理解相似三角形的性质,对应角相等,对应边成比例。2、掌握相似三角形的性质,对应高的比,对应角平分线的比,对应中线的比都等于相似比。
【温故知新】:相似三角形性质:(1)边:对应边成比例。(2)角:对应角相等。(3)高:相似三角形对应边上的高之比等于相似比。(4)中线:相似三角形对应边上的中线比等于相似比。(5)角平分线:相似三角形对应角的角平分线之比等于相似比。【自主探究】:1、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是2:3,AD、A′D′是对应高(对应边上的高),(1)问△ABD与△A′B′D′相似吗 (2)求:AD:A′D′ 2、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是k,AD、A′D′是对应角平分线(对应角的角平分线),(1) 问△ABD与△A′B′D′相似吗 (2) 求:AD:A′D′ 3、已知:△ABC∽△A′B′C′,△ABC和△A′B′C′的相似比是k, AD、A′D′是对应中线(对应边上的中线),(1)问△ABD与△A′B′D′相似吗 (2) 求:AD:A′D′【拓展应用】1、 △ABC与△A'B'C'的相似比1:3,若BC=5cm,则B'C'=_____ 。
2、如果两个相似三角形的对应高的比为2:3,那么对应角平分线的比是__ ,对应边上的中线的比是______ 。 3、△ABC与△A'B'C'的相似比3:4,若BC边上的高AD=12cm,则B'C'边上的高A'D'=_____ 。4、如图所示,在△ABC中,边BC=60cm,高AD=40cm,正方形PQRS的一边PQ在BC上,另两个顶点S,R分别在AB,AC上,SR与AD相交于点E.(1) △ASR与 △ABC相似吗 为什么 (2)求正方形PQRS的边长?【课堂检测】:1、△ABC∽△A`B`C`,AD和A`D`分别是BC和B`C`边上的高,AE和A`E`分别是BC边和B`C`边上的中线,AD:A`D`=3:5,则AE:A`E`=_______,△ A`B`C 和△ABC的相似比是_________.2、电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,(1)若点P到CD的距离为3m。求P到AB的距离?(2)若PE⊥CD于D交AB于F,EF=1m,求PF
自我评价专栏 自主学习: 合作与交流: 书写: 综合:
A′
C′
D′
B′
B
C
D
A
A′
C′
D′
B′
C
D
A
B
A′
C′
D′
B′
C
D
A
B
B
A
D
R
S
C
P
Q
E
D
E
F
C
A
B
P
