2.1.2 两条直线平行与垂直 课件(共14张PPT)
文档属性
| 名称 | 2.1.2 两条直线平行与垂直 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 713.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 06:23:26 | ||
图片预览



文档简介
(共14张PPT)
2.1.2
两条直线平行与垂直的判定
XXXX学校 XXX
2023.09
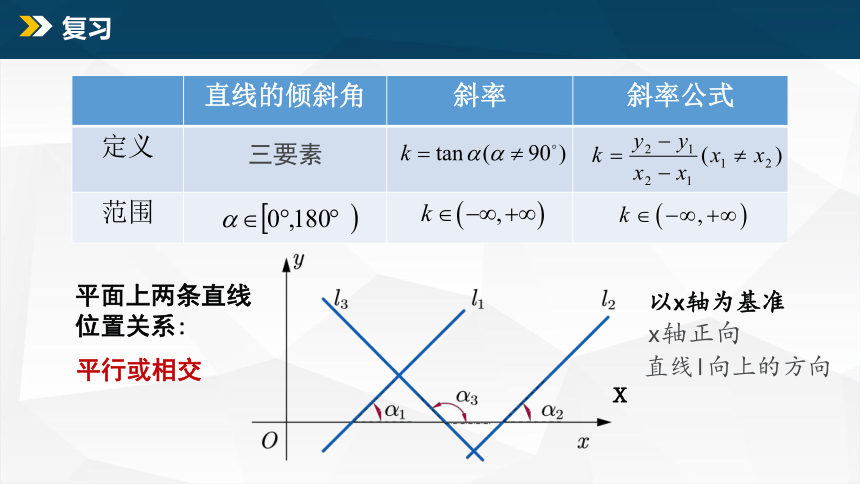
复面上两条直线位置关系:
直线的倾斜角 斜率 斜率公式
定义
范围
三要素
x
以x轴为基准
x轴正向
直线l向上的方向
平行或相交
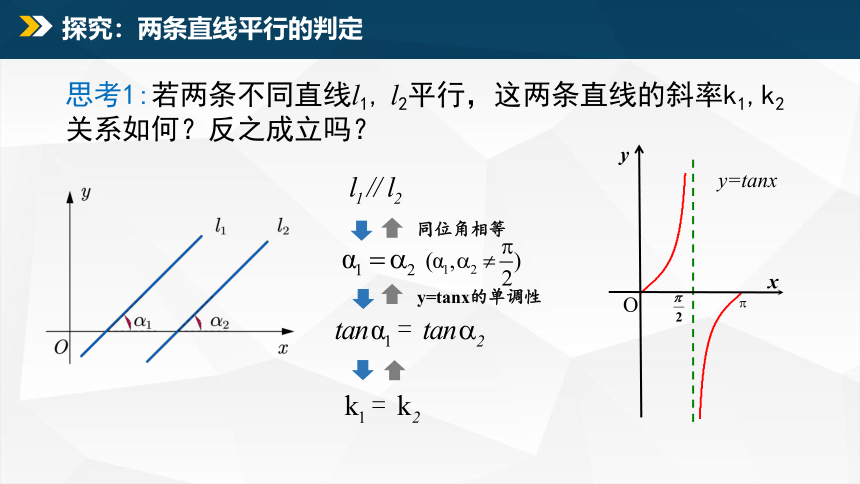
思考1:若两条不同直线l1, l2平行,这两条直线的斜率k1,k2关系如何?反之成立吗?
y=tanx的单调性
同位角相等
探究:两条直线平行的判定
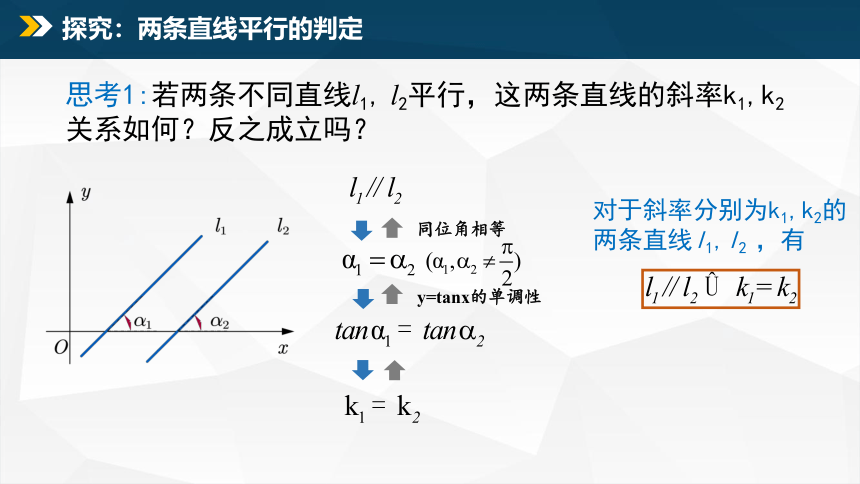
思考1:若两条不同直线l1, l2平行,这两条直线的斜率k1,k2关系如何?反之成立吗?
对于斜率分别为k1,k2的两条直线l1,l2 ,有
同位角相等
y=tanx的单调性
探究:两条直线平行的判定
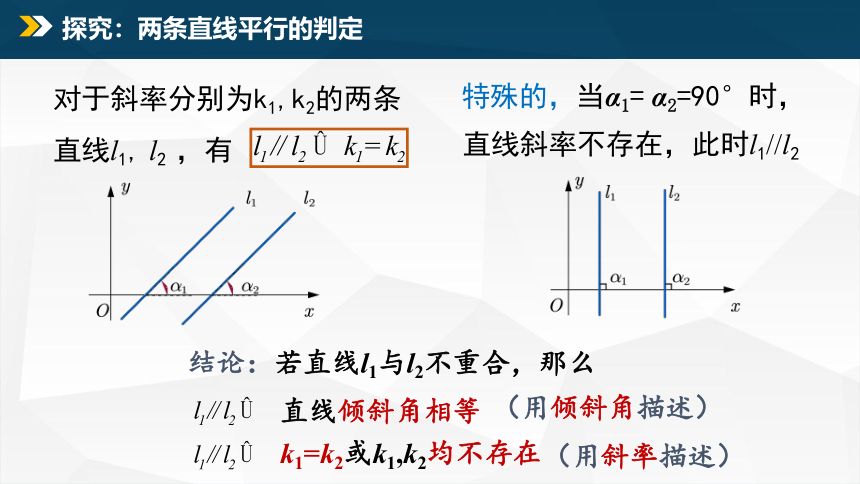
特殊的,当α1= α2=90°时,
对于斜率分别为k1,k2的两条直线l1, l2 ,有
直线斜率不存在,此时l1//l2
结论:若直线l1与l2不重合,那么
直线倾斜角相等
k1=k2或k1,k2均不存在
探究:两条直线平行的判定
(用倾斜角描述)
(用斜率描述)
例1 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
应用:两条直线平行的判定
应用:两条直线平行的判定
练习2 在△ABC中,A(0,3),B(2,-1),E,F分别为边AC,BC的中点,则直线EF的斜率为________.
练习3 已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,则m的值为_______.
思考2 两条不重合的直线,斜率分别为k1,k2,
那么l1⊥l2时,k1与k2满足什么关系?
对于斜率分别为k1,k2的两条直线l1,l2 ,有
探究:两条直线垂直的判定
特殊的,当α1= 90°,α2=0 °时,
l1斜率不存在, l2斜率为0,此时l1⊥l2
对于斜率分别为k1,k2的两条直线l1,l2 ,有
k1·k2 =-1
一条斜率为0,另一条斜率不存在
探究:两条直线垂直的判定
对于两个非零向量a=(x1,y1), b =(x2, y2) ,有:
思考:对于上述结论,你还有其他的证明方法吗?
对于斜率分别为k1,k2的两条直线l1,l2 ,有:
a=(1,k1), b =(1, k2)
∴a· b =(1,k1) · (1, k2)
=1+k1·k2 =0
∵a⊥b
a
b
探究:两条直线垂直的判定
应用:两条直线垂直的判定
例2 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系,并证明你的结论.
练习1 l1经过点A(3,4),B(3,10);l2经过点M(-10,40),N(10,40),那么l1与l2是否垂直?
应用:两条直线垂直的判定
练习3 已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2),如果l1⊥l2,则a的值为____.
练习2 若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线的斜率为__________.
等价问法: P (a,b) ,Q (3-b,3-a)两点关于直线l对称,求直线l的斜率.
综合应用:两条直线平行与垂直
1.已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为______.
2.直线l1,l2的斜率k1,k2是关于k的方程2k2-3k-b=0的两根,若l1⊥l2,则b=__________;若l1∥l2,则b=__________.
3.已知四边形ABCD的顶点B(6,-1),C(5,2), D(1,2).若四边形ABCD为直角梯形,求A点坐标.
总结
直线的斜率
直线的倾斜角
“形”
“数”
判断两条直线的位置关系
k1·k2 =-1
一条斜率为0,
另一条斜率不存在
k1,k2均不存在
k1=k2
2.1.2
两条直线平行与垂直的判定
XXXX学校 XXX
2023.09
复面上两条直线位置关系:
直线的倾斜角 斜率 斜率公式
定义
范围
三要素
x
以x轴为基准
x轴正向
直线l向上的方向
平行或相交
思考1:若两条不同直线l1, l2平行,这两条直线的斜率k1,k2关系如何?反之成立吗?
y=tanx的单调性
同位角相等
探究:两条直线平行的判定
思考1:若两条不同直线l1, l2平行,这两条直线的斜率k1,k2关系如何?反之成立吗?
对于斜率分别为k1,k2的两条直线l1,l2 ,有
同位角相等
y=tanx的单调性
探究:两条直线平行的判定
特殊的,当α1= α2=90°时,
对于斜率分别为k1,k2的两条直线l1, l2 ,有
直线斜率不存在,此时l1//l2
结论:若直线l1与l2不重合,那么
直线倾斜角相等
k1=k2或k1,k2均不存在
探究:两条直线平行的判定
(用倾斜角描述)
(用斜率描述)
例1 已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
应用:两条直线平行的判定
应用:两条直线平行的判定
练习2 在△ABC中,A(0,3),B(2,-1),E,F分别为边AC,BC的中点,则直线EF的斜率为________.
练习3 已知A(m,3),B(2m,m+4),C(m+1,2),D(1,0),且直线AB与直线CD平行,则m的值为_______.
思考2 两条不重合的直线,斜率分别为k1,k2,
那么l1⊥l2时,k1与k2满足什么关系?
对于斜率分别为k1,k2的两条直线l1,l2 ,有
探究:两条直线垂直的判定
特殊的,当α1= 90°,α2=0 °时,
l1斜率不存在, l2斜率为0,此时l1⊥l2
对于斜率分别为k1,k2的两条直线l1,l2 ,有
k1·k2 =-1
一条斜率为0,另一条斜率不存在
探究:两条直线垂直的判定
对于两个非零向量a=(x1,y1), b =(x2, y2) ,有:
思考:对于上述结论,你还有其他的证明方法吗?
对于斜率分别为k1,k2的两条直线l1,l2 ,有:
a=(1,k1), b =(1, k2)
∴a· b =(1,k1) · (1, k2)
=1+k1·k2 =0
∵a⊥b
a
b
探究:两条直线垂直的判定
应用:两条直线垂直的判定
例2 已知A(-6,0),B(3,6),P(0,3),Q(6,-6),试判断直线AB与PQ的位置关系,并证明你的结论.
练习1 l1经过点A(3,4),B(3,10);l2经过点M(-10,40),N(10,40),那么l1与l2是否垂直?
应用:两条直线垂直的判定
练习3 已知直线l1经过点A(3,a),B(a-2,-3),直线l2经过点C(2,3),D(-1,a-2),如果l1⊥l2,则a的值为____.
练习2 若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线的斜率为__________.
等价问法: P (a,b) ,Q (3-b,3-a)两点关于直线l对称,求直线l的斜率.
综合应用:两条直线平行与垂直
1.已知A(1,0),B(3,2),C(0,4),点D满足AB⊥CD,且AD∥BC,则点D的坐标为______.
2.直线l1,l2的斜率k1,k2是关于k的方程2k2-3k-b=0的两根,若l1⊥l2,则b=__________;若l1∥l2,则b=__________.
3.已知四边形ABCD的顶点B(6,-1),C(5,2), D(1,2).若四边形ABCD为直角梯形,求A点坐标.
总结
直线的斜率
直线的倾斜角
“形”
“数”
判断两条直线的位置关系
k1·k2 =-1
一条斜率为0,
另一条斜率不存在
k1,k2均不存在
k1=k2
