1.3 空间向量及其运算的坐标表示 课件(共14张PPT)
文档属性
| 名称 | 1.3 空间向量及其运算的坐标表示 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 599.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 08:10:31 | ||
图片预览



文档简介
(共14张PPT)
XXXX学校 XXX
2023.09
1.3.1
空间直角坐标系
在空间取定一点O
从O出发引三条两两垂直的直线
选定某个长度作为单位长度
(原点)
(坐标轴)
O
x
y
z
1
1
1
右手系
X
Y
Z
作图:
一般的
01 空间直角坐标系的建立
Ⅱ
Ⅶ
xOz面
Ⅴ
Ⅵ
Ⅰ
xOy面
yOz面
Ⅲ
Ⅳ
Ⅷ
O
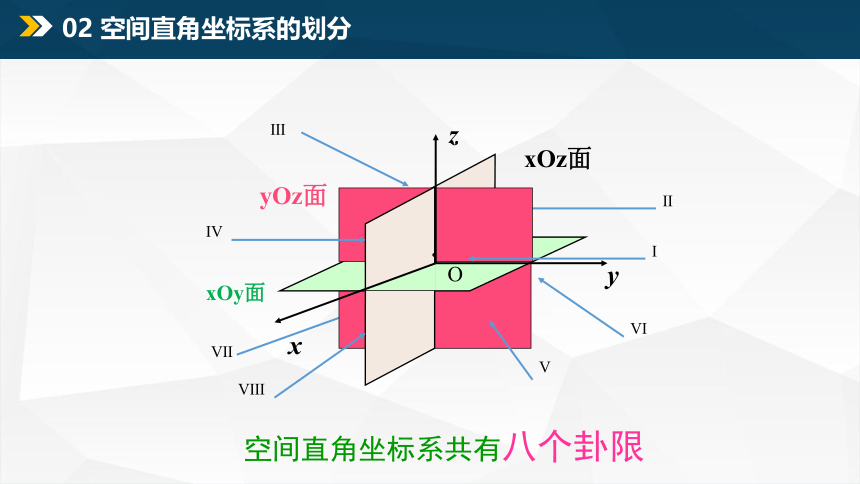
空间直角坐标系共有八个卦限
02 空间直角坐标系的划分
1
1
1
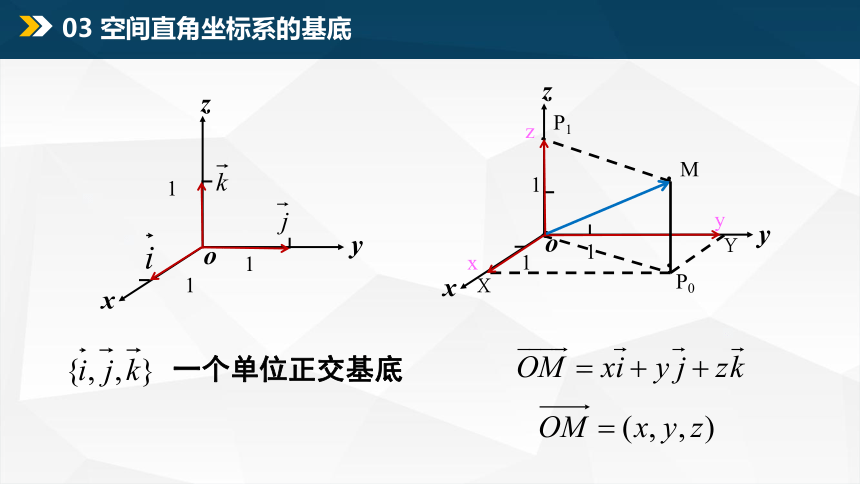
一个单位正交基底
1
1
1
M
P0
x
y
z
P1
X
Y
03 空间直角坐标系的基底
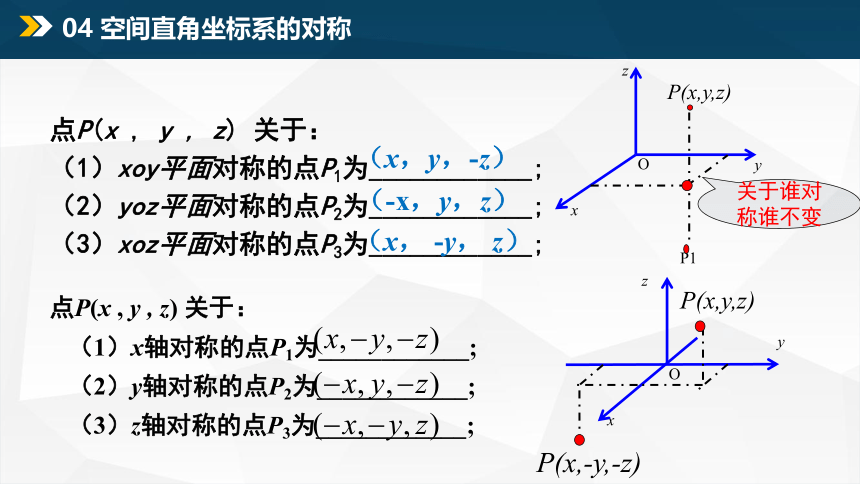
点P(x , y , z) 关于:
(1)xoy平面对称的点P1为____________;
(2)yoz平面对称的点P2为____________;
(3)xoz平面对称的点P3为____________;
关于谁对称谁不变
(x,y,-z)
(-x,y,z)
(x, -y, z)
O
x
y
z
P(x,y,z)
P1
点P(x , y , z) 关于:
(1)x轴对称的点P1为____________;
(2)y轴对称的点P2为____________;
(3)z轴对称的点P3为____________;
O
x
y
z
P(x,y,z)
P(x,-y,-z)
04 空间直角坐标系的对称
O
x
y
z
O
x
y
z
【练习1】如图,PA垂直于正方形ABCD所在的平面,M,N分别是AB,PC的中点,并且PA=AB=1,试建立适当的空间直角坐标系,求向量 的坐标.
以A为原点,AD,AB,AP所在直线为坐标轴建立空间直角坐标系如图所示.
已知
【练习2】如图所示,在三棱锥O-ABC中,OA,OB,OC两两垂直,OA=1,OB=2,OC=3,E,F分别为AC,BC的中点,建立以 方向上的单位向量为正交基底的空间直角坐标系Oxyz,求EF中点P的坐标.
已知
A,B中点
z
x
y
O
P2(x2,y2,z2)
(1) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:
N
P1(x1,y1,z1)
M
H
04 空间的两点间距离公式
【典例】如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求线段MN的长度.
1.3.2
空间向量运算的坐标表示
01 向量的直角坐标运算
02 空间向量的距离与夹角
1.距离公式
(1)向量的长度(模)公式
x
z
y
O
P(x,y,z)
P`
注意:此公式的几何意义是表示长方体的对角线的长度。
(2)空间两点间的距离公式
在空间直角坐标系中,已知 、 ,则
02 空间向量的距离与夹角
两个向量夹角公式
注意:
(1)当 时, 同向;
(2)当 时, 反向;
(3)当 时, 。
XXXX学校 XXX
2023.09
1.3.1
空间直角坐标系
在空间取定一点O
从O出发引三条两两垂直的直线
选定某个长度作为单位长度
(原点)
(坐标轴)
O
x
y
z
1
1
1
右手系
X
Y
Z
作图:
一般的
01 空间直角坐标系的建立
Ⅱ
Ⅶ
xOz面
Ⅴ
Ⅵ
Ⅰ
xOy面
yOz面
Ⅲ
Ⅳ
Ⅷ
O
空间直角坐标系共有八个卦限
02 空间直角坐标系的划分
1
1
1
一个单位正交基底
1
1
1
M
P0
x
y
z
P1
X
Y
03 空间直角坐标系的基底
点P(x , y , z) 关于:
(1)xoy平面对称的点P1为____________;
(2)yoz平面对称的点P2为____________;
(3)xoz平面对称的点P3为____________;
关于谁对称谁不变
(x,y,-z)
(-x,y,z)
(x, -y, z)
O
x
y
z
P(x,y,z)
P1
点P(x , y , z) 关于:
(1)x轴对称的点P1为____________;
(2)y轴对称的点P2为____________;
(3)z轴对称的点P3为____________;
O
x
y
z
P(x,y,z)
P(x,-y,-z)
04 空间直角坐标系的对称
O
x
y
z
O
x
y
z
【练习1】如图,PA垂直于正方形ABCD所在的平面,M,N分别是AB,PC的中点,并且PA=AB=1,试建立适当的空间直角坐标系,求向量 的坐标.
以A为原点,AD,AB,AP所在直线为坐标轴建立空间直角坐标系如图所示.
已知
【练习2】如图所示,在三棱锥O-ABC中,OA,OB,OC两两垂直,OA=1,OB=2,OC=3,E,F分别为AC,BC的中点,建立以 方向上的单位向量为正交基底的空间直角坐标系Oxyz,求EF中点P的坐标.
已知
A,B中点
z
x
y
O
P2(x2,y2,z2)
(1) 在空间直角坐标系中,任意两点P1(x1,y1,z1)和P2(x2,y2,z2)间的距离:
N
P1(x1,y1,z1)
M
H
04 空间的两点间距离公式
【典例】如图所示,在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=2,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求线段MN的长度.
1.3.2
空间向量运算的坐标表示
01 向量的直角坐标运算
02 空间向量的距离与夹角
1.距离公式
(1)向量的长度(模)公式
x
z
y
O
P(x,y,z)
P`
注意:此公式的几何意义是表示长方体的对角线的长度。
(2)空间两点间的距离公式
在空间直角坐标系中,已知 、 ,则
02 空间向量的距离与夹角
两个向量夹角公式
注意:
(1)当 时, 同向;
(2)当 时, 反向;
(3)当 时, 。
