2.2.1-3 直线的点斜式、两点式、一般式方程 课件(共24张PPT)
文档属性
| 名称 | 2.2.1-3 直线的点斜式、两点式、一般式方程 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1009.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 08:11:06 | ||
图片预览







文档简介
(共24张PPT)
2.2.1
直线的点斜式方程
XXXX学校 XXX
2023.09
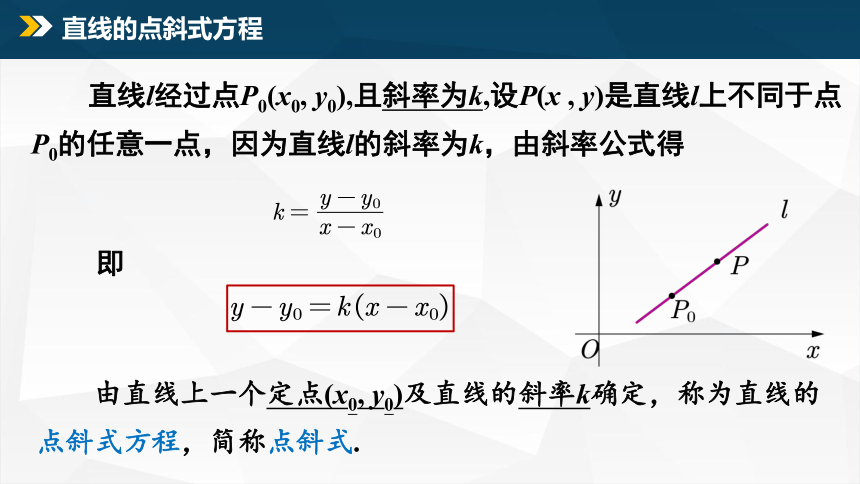
直线l经过点P0(x0, y0),且斜率为k,设P(x , y)是直线l上不同于点P0的任意一点,因为直线l的斜率为k,由斜率公式得
直线的点斜式方程
即
由直线上一个定点(x0, y0)及直线的斜率k确定,称为直线的点斜式方程,简称点斜式.
斜率存在
x-x0=0,即x=x0
(1) 利用点斜式表示直线方程的前提是什么
(2) 直线l过点P0(x0, y0),当倾斜角为0°时直线的方程是什么
y-y0=0,即y=y0
(3)直线l经过点P0(x0,y0),当倾斜角为90°时直线的方程是什么
直线的点斜式方程
直线l的斜率为k,且与y轴的交点为(0,b),则直线的斜截式方程为y=kx+b,其中b叫做直线l在y轴上的截距.
直线的斜截式方程
特殊化
【思考】(1)直线的斜截式方程y=kx+b中, k和b的几何意义是什么
k:直线的斜率;
b:直线在y轴上的截距.
(2)截距是距离吗
不是,直线在y轴上的截距是直线与y轴交点的纵坐标,截距是实数而不是距离.
直线的斜截式方程
补充:直线l过定点A(-2,3),并且与两条坐标轴围成的三角形面积为4,求直线l的方程.
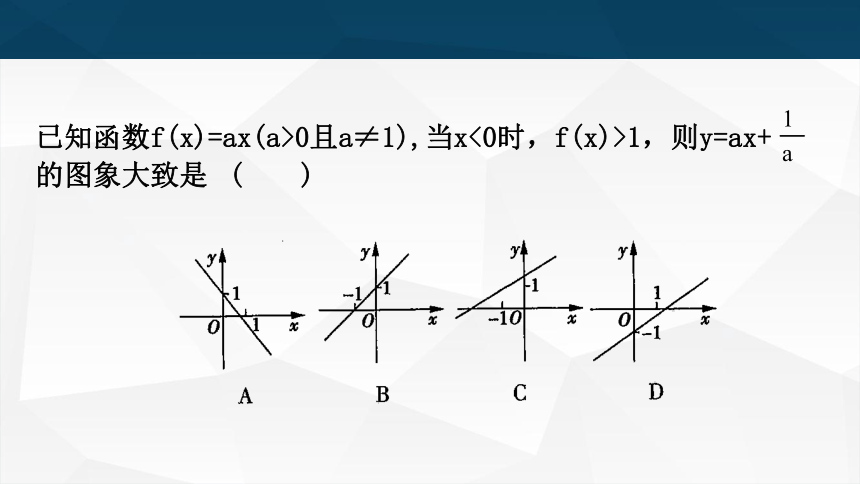
已知函数f(x)=ax(a>0且a≠1),当x<0时,f(x)>1,则y=ax+ 的图象大致是 ( )
北京师范大学南山附属学校 陈诗韵
2023.09
3.2.2
直线的两点式方程
00 复习
点斜式方程:y- y0 =k(x- x0 )
k为斜率, P0(x0 ,y0)为直线上的一定点
截距式方程:y=kx+b
k为斜率,b为截距
01 两点式方程
例1.已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
解:设直线方程为:y=kx+b
由已知得:
解方程组得:
所以,直线方程为: y=x+2
方程思想
由斜率公式得斜率
直线的点斜式方程为
所以,直线方程为: y=x+2
01 两点式方程
例1.已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
设P(x,y)为直线上不同于P1 , P2的动点,与P1(1,3)P2(2,4)在同一直线上,根据斜率相等可得:
即:
得: y=x+2
推广 已知直线经过P1(x1, y1)和P2(x2, y2)两点,求直线的方程.
即:
两点式方程
01 两点式方程
思考:是不是已知任一直线中的两点就能用两点式 写出直线方程呢?
当x1 =x2或y1= y2时,直线P1 P2没有两点式方程.
注:两点式不能表示平行于坐标轴或与坐标轴重合的直线.
已知直线 l 与x轴的交点为A(a, 0),与y轴的交点为B(0, b),其中a≠0,b≠0,求直线l 的方程.
解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:
即
注:直线与 x 轴的交点(a, o)的横坐标 a 叫做直线在 x 轴上的截距
直线与 y 轴的交点(0, b)的纵坐标 b 叫做直线在 y 轴上的截距
ab≠0
02 截距式方程
图象的辨析【典例】两条直线l1: =1和
l2: =1在同一直角坐标系中的图象可以是( )
北京师范大学南山附属学校 陈诗韵
2023.09
3.2.3
直线的一般式方程
名称 已知条件 方程 适用范围
斜率k与点(x0,y0)
斜率k与纵截距b
两点(x1,y1),(x2,y2)
横(纵)截距a与b
y-y0=k(x-x0)
y=kx+b
不含垂直于x轴的直线
不含垂直于坐标轴和过原点的直线
不含垂直于x轴的直线
不含垂直于坐标轴的直线
点斜式
斜截式
两点式
截距式
00 复习
直线的四种方程形式均是二元一次方程.
若直线l过点A(2,0), B(0,2),分别写出直线l的点斜式、斜截式、两点式、截距式方程
00 复习
01 一般式方程
思考:
(1)平面直角坐标系中的任意一条直线都可以用一个关于x, y的二元一次方程表示吗?
(2)任意一个关于x, y的二元一次方程都能表示一条直线吗?
我们把关于x, y的二元一次方程Ax+ By+C=0 的二元一次方程(A, B不同时为0)叫做直线的一般式方程,简称一般式.
当B≠0 时, ,表示过点 ,斜率为 的直线.
当B=0 时, ,表示过点 ,且垂直于x轴的直线.
01 一般式方程
探究:
在Ax+ By+C=0 方程中,A,B,C为何值时,方程表示的直线:
①平行于x轴? ②平行于y轴? ③与x轴重合? ④与y轴重合?
A=0 ,B≠0, C≠0
By+C=0
A≠0 ,B=0, C≠0
Ax+C=0
形如:y=a(a≠0)
形如:x=a(x≠0)
y=0
x=0
A=0 ,B≠0, C=0
By=0
A≠0 ,B=0, C=0
Ax=0
注:一般式方程Ax+ By+C=0(A, B不同时为0)可以表示平面直角坐标系中所有直线!
一般式
两点或一个点和斜率或横纵截距
Ax+By+C=0
(A2+B2≠0)
平面直角坐标系内的所有直线都适用
01 一般式方程
平行:
重合:
垂直:
01 一般式方程
探究:已知直线l1:A1x+ B1y+C1=0 ,直线l2:A2x+ B2y+C2=0,那么两直线满足下列位置关系时的条件是什么?
①l1与l2重合 ②l1//l2 ③l1⊥l2
2.2.1
直线的点斜式方程
XXXX学校 XXX
2023.09
直线l经过点P0(x0, y0),且斜率为k,设P(x , y)是直线l上不同于点P0的任意一点,因为直线l的斜率为k,由斜率公式得
直线的点斜式方程
即
由直线上一个定点(x0, y0)及直线的斜率k确定,称为直线的点斜式方程,简称点斜式.
斜率存在
x-x0=0,即x=x0
(1) 利用点斜式表示直线方程的前提是什么
(2) 直线l过点P0(x0, y0),当倾斜角为0°时直线的方程是什么
y-y0=0,即y=y0
(3)直线l经过点P0(x0,y0),当倾斜角为90°时直线的方程是什么
直线的点斜式方程
直线l的斜率为k,且与y轴的交点为(0,b),则直线的斜截式方程为y=kx+b,其中b叫做直线l在y轴上的截距.
直线的斜截式方程
特殊化
【思考】(1)直线的斜截式方程y=kx+b中, k和b的几何意义是什么
k:直线的斜率;
b:直线在y轴上的截距.
(2)截距是距离吗
不是,直线在y轴上的截距是直线与y轴交点的纵坐标,截距是实数而不是距离.
直线的斜截式方程
补充:直线l过定点A(-2,3),并且与两条坐标轴围成的三角形面积为4,求直线l的方程.
已知函数f(x)=ax(a>0且a≠1),当x<0时,f(x)>1,则y=ax+ 的图象大致是 ( )
北京师范大学南山附属学校 陈诗韵
2023.09
3.2.2
直线的两点式方程
00 复习
点斜式方程:y- y0 =k(x- x0 )
k为斜率, P0(x0 ,y0)为直线上的一定点
截距式方程:y=kx+b
k为斜率,b为截距
01 两点式方程
例1.已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
解:设直线方程为:y=kx+b
由已知得:
解方程组得:
所以,直线方程为: y=x+2
方程思想
由斜率公式得斜率
直线的点斜式方程为
所以,直线方程为: y=x+2
01 两点式方程
例1.已知直线经过P1(1,3)和P2(2,4)两点,求直线的方程.
设P(x,y)为直线上不同于P1 , P2的动点,与P1(1,3)P2(2,4)在同一直线上,根据斜率相等可得:
即:
得: y=x+2
推广 已知直线经过P1(x1, y1)和P2(x2, y2)两点,求直线的方程.
即:
两点式方程
01 两点式方程
思考:是不是已知任一直线中的两点就能用两点式 写出直线方程呢?
当x1 =x2或y1= y2时,直线P1 P2没有两点式方程.
注:两点式不能表示平行于坐标轴或与坐标轴重合的直线.
已知直线 l 与x轴的交点为A(a, 0),与y轴的交点为B(0, b),其中a≠0,b≠0,求直线l 的方程.
解:将两点A(a,0), B(0,b)的坐标代入两点式, 得:
即
注:直线与 x 轴的交点(a, o)的横坐标 a 叫做直线在 x 轴上的截距
直线与 y 轴的交点(0, b)的纵坐标 b 叫做直线在 y 轴上的截距
ab≠0
02 截距式方程
图象的辨析【典例】两条直线l1: =1和
l2: =1在同一直角坐标系中的图象可以是( )
北京师范大学南山附属学校 陈诗韵
2023.09
3.2.3
直线的一般式方程
名称 已知条件 方程 适用范围
斜率k与点(x0,y0)
斜率k与纵截距b
两点(x1,y1),(x2,y2)
横(纵)截距a与b
y-y0=k(x-x0)
y=kx+b
不含垂直于x轴的直线
不含垂直于坐标轴和过原点的直线
不含垂直于x轴的直线
不含垂直于坐标轴的直线
点斜式
斜截式
两点式
截距式
00 复习
直线的四种方程形式均是二元一次方程.
若直线l过点A(2,0), B(0,2),分别写出直线l的点斜式、斜截式、两点式、截距式方程
00 复习
01 一般式方程
思考:
(1)平面直角坐标系中的任意一条直线都可以用一个关于x, y的二元一次方程表示吗?
(2)任意一个关于x, y的二元一次方程都能表示一条直线吗?
我们把关于x, y的二元一次方程Ax+ By+C=0 的二元一次方程(A, B不同时为0)叫做直线的一般式方程,简称一般式.
当B≠0 时, ,表示过点 ,斜率为 的直线.
当B=0 时, ,表示过点 ,且垂直于x轴的直线.
01 一般式方程
探究:
在Ax+ By+C=0 方程中,A,B,C为何值时,方程表示的直线:
①平行于x轴? ②平行于y轴? ③与x轴重合? ④与y轴重合?
A=0 ,B≠0, C≠0
By+C=0
A≠0 ,B=0, C≠0
Ax+C=0
形如:y=a(a≠0)
形如:x=a(x≠0)
y=0
x=0
A=0 ,B≠0, C=0
By=0
A≠0 ,B=0, C=0
Ax=0
注:一般式方程Ax+ By+C=0(A, B不同时为0)可以表示平面直角坐标系中所有直线!
一般式
两点或一个点和斜率或横纵截距
Ax+By+C=0
(A2+B2≠0)
平面直角坐标系内的所有直线都适用
01 一般式方程
平行:
重合:
垂直:
01 一般式方程
探究:已知直线l1:A1x+ B1y+C1=0 ,直线l2:A2x+ B2y+C2=0,那么两直线满足下列位置关系时的条件是什么?
①l1与l2重合 ②l1//l2 ③l1⊥l2
