人教版数学九年级上册 24.1.1 圆 同步练习(含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.1.1 圆 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 466.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 11:05:51 | ||
图片预览

文档简介
24.1.1 圆
一、基础题
1.下列命题正确的有( )
(1)半圆是弧;
(2)弦是圆上两点之间的部分;
(3)半径是弦;
(4)直径是最长的弦;
(5)在同一平面内,到定点的距离等于定长的点都在同一个圆上.
A.1个 B.2个 C.3个 D.4个
2.如图24-1-1所示,⊙O中点A,O,D以及点B,O,C分别在同一直线上,图中弦的条数为( )
A.2 B.3 C.4 D.5
图24-1-1
3.如图24-1-2,P是⊙O内的一点,P到⊙O的最小距离为4 cm,最大距离为9 cm,则该⊙O的直径为( )
A.6.5 cm B.2.5 cm C.13 cm D.不可求
图24-1-2
4.图24-1-3中,____是⊙O的直径;弦有____;劣弧有___;优弧有____.
图24-1-3
5.如图24-1-4所示,已知∠AOB=60°,则△AOB是____三角形.
图24-1-4
6.如图24-1-5,AB是⊙O的直径,AC是弦,若∠ACO=22°, 则∠COB的度数等于____.
图24-1-5
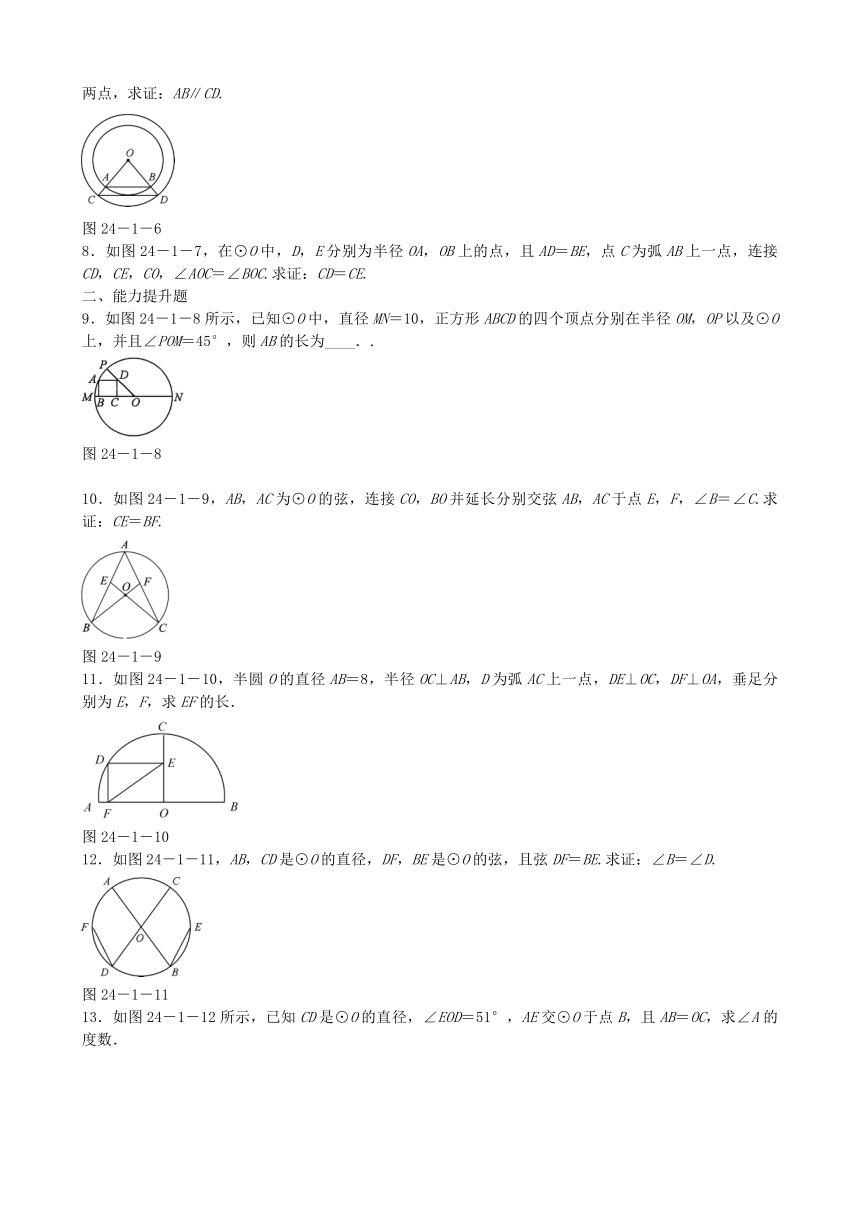
7.如图24-1-6,以O为圆心的两个同心圆⊙O,大圆O的半径OC,OD分别交小圆O于A,B
两点,求证:AB∥CD.
图24-1-6
8.如图24-1-7,在⊙O中,D,E分别为半径OA,OB上的点,且AD=BE,点C为弧AB上一点,连接CD,CE,CO,∠AOC=∠BOC.求证:CD=CE.
二、能力提升题
9.如图24-1-8所示,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM,OP以及⊙O上,并且∠POM=45°,则AB的长为____..
图24-1-8
10.如图24-1-9,AB,AC为⊙O的弦,连接CO,BO并延长分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
图24-1-9
11.如图24-1-10,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E,F,求EF的长.
图24-1-10
12.如图24-1-11,AB,CD是⊙O的直径,DF,BE是⊙O的弦,且弦DF=BE.求证:∠B=∠D.
图24-1-11
13.如图24-1-12所示,已知CD是⊙O的直径,∠EOD=51°,AE交⊙O于点B,且AB=OC,求∠A的度数.
图24-1-12
答案:
1.C 2.A 3.C 4.AC AB,BC,AC ,
5. 等边 6.44°
7.证明:∵OA=OB,OC=OD,
∴∠OAB=(180°-∠O)=∠C,∴AB∥CD.
图24-1-7
8.证明:∵OA=OB,AD=BE,∴OA-AD=OB-BE,即OD=OE.
在△ODC和△OEC中,
∴△ODC≌△OEC,∴CD=CE.
9.
10.证明:∵OB,OC是⊙O的半径,∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC,∴OE=OF,∴CE=BF.
11.解:连接OD.
∵OC⊥AB,DE⊥OC,DF⊥OA,
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,∴EF=OD.
∵OD=OA,∴EF=OA=4.
12.证明:如图,连接OE,OF.在△DOF和△BOE中,
∴△DOF≌△BOE(SSS).
∴∠B=∠D.
13.
解:如图所示,连接OB.∵AB=OC,OB=OC,
∴AB=OB,
∴∠A=∠1.
又∵OB=OE,
∴∠E=∠2=∠1+∠A=2∠A,
∴∠DOE=∠E+∠A=3∠A.而∠DOE=51°,
∴3∠A=51°,
∴∠A=17°.
一、基础题
1.下列命题正确的有( )
(1)半圆是弧;
(2)弦是圆上两点之间的部分;
(3)半径是弦;
(4)直径是最长的弦;
(5)在同一平面内,到定点的距离等于定长的点都在同一个圆上.
A.1个 B.2个 C.3个 D.4个
2.如图24-1-1所示,⊙O中点A,O,D以及点B,O,C分别在同一直线上,图中弦的条数为( )
A.2 B.3 C.4 D.5
图24-1-1
3.如图24-1-2,P是⊙O内的一点,P到⊙O的最小距离为4 cm,最大距离为9 cm,则该⊙O的直径为( )
A.6.5 cm B.2.5 cm C.13 cm D.不可求
图24-1-2
4.图24-1-3中,____是⊙O的直径;弦有____;劣弧有___;优弧有____.
图24-1-3
5.如图24-1-4所示,已知∠AOB=60°,则△AOB是____三角形.
图24-1-4
6.如图24-1-5,AB是⊙O的直径,AC是弦,若∠ACO=22°, 则∠COB的度数等于____.
图24-1-5
7.如图24-1-6,以O为圆心的两个同心圆⊙O,大圆O的半径OC,OD分别交小圆O于A,B
两点,求证:AB∥CD.
图24-1-6
8.如图24-1-7,在⊙O中,D,E分别为半径OA,OB上的点,且AD=BE,点C为弧AB上一点,连接CD,CE,CO,∠AOC=∠BOC.求证:CD=CE.
二、能力提升题
9.如图24-1-8所示,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM,OP以及⊙O上,并且∠POM=45°,则AB的长为____..
图24-1-8
10.如图24-1-9,AB,AC为⊙O的弦,连接CO,BO并延长分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
图24-1-9
11.如图24-1-10,半圆O的直径AB=8,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥OA,垂足分别为E,F,求EF的长.
图24-1-10
12.如图24-1-11,AB,CD是⊙O的直径,DF,BE是⊙O的弦,且弦DF=BE.求证:∠B=∠D.
图24-1-11
13.如图24-1-12所示,已知CD是⊙O的直径,∠EOD=51°,AE交⊙O于点B,且AB=OC,求∠A的度数.
图24-1-12
答案:
1.C 2.A 3.C 4.AC AB,BC,AC ,
5. 等边 6.44°
7.证明:∵OA=OB,OC=OD,
∴∠OAB=(180°-∠O)=∠C,∴AB∥CD.
图24-1-7
8.证明:∵OA=OB,AD=BE,∴OA-AD=OB-BE,即OD=OE.
在△ODC和△OEC中,
∴△ODC≌△OEC,∴CD=CE.
9.
10.证明:∵OB,OC是⊙O的半径,∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC,∴OE=OF,∴CE=BF.
11.解:连接OD.
∵OC⊥AB,DE⊥OC,DF⊥OA,
∴∠AOC=∠DEO=∠DFO=90°,
∴四边形DEOF是矩形,∴EF=OD.
∵OD=OA,∴EF=OA=4.
12.证明:如图,连接OE,OF.在△DOF和△BOE中,
∴△DOF≌△BOE(SSS).
∴∠B=∠D.
13.
解:如图所示,连接OB.∵AB=OC,OB=OC,
∴AB=OB,
∴∠A=∠1.
又∵OB=OE,
∴∠E=∠2=∠1+∠A=2∠A,
∴∠DOE=∠E+∠A=3∠A.而∠DOE=51°,
∴3∠A=51°,
∴∠A=17°.
同课章节目录
