9.2三角形的内角与外角 同步练习题 冀教版七年级数学下册(含答案)
文档属性
| 名称 | 9.2三角形的内角与外角 同步练习题 冀教版七年级数学下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 16:37:20 | ||
图片预览



文档简介
冀教版七年级数学下册《9.2三角形的内角与外角》同步练习题(附答案)
一.选择题(共10小题,满分30分)
1.在△ABC中,∠B=45°,∠C的外角等于100°,则∠A的度数是( )
A.65° B.55° C.54° D.35°
2.若一个三角形的三个内角度数的比为2:3:5,那么这个三角形的最大内角的度数为( )
A.54° B.60° C.90° D.100°
3.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠1=70°,则∠C的大小为( )
A.40° B.50° C.75° D.85°
4.如图,下列关于∠A,∠B,∠C,∠1的关系中一定成立的是( )
A.∠A+∠B=∠C+∠1 B.∠A+∠1=∠B+∠C
C.∠A+∠B+∠C=∠1 D.∠A+∠B+∠C+∠1=360°
5.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.则下列结论正确的是( )
A.∠1>∠D B.∠D>∠2 C.∠1=∠2+∠3 D.∠3=∠A
6.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线.∠BAC=50°,∠ABC=60°.则∠DAE+∠ACD等于( )
A.75° B.80° C.85° D.90°
7.如图所示,一副三角板叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.135°
8.如图,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2021BC与∠A2021CD的平分线相交于点A2022,得∠A2022,则∠A2022是( )度.
A.x B.x C.x D.x
9.如图,在△ABC中,∠C=90°,∠A=30°,将△ABC沿直线m翻折,点A落在点D的位置,则∠1﹣∠2的度数是( )
A.30° B.45° C.60° D.75°
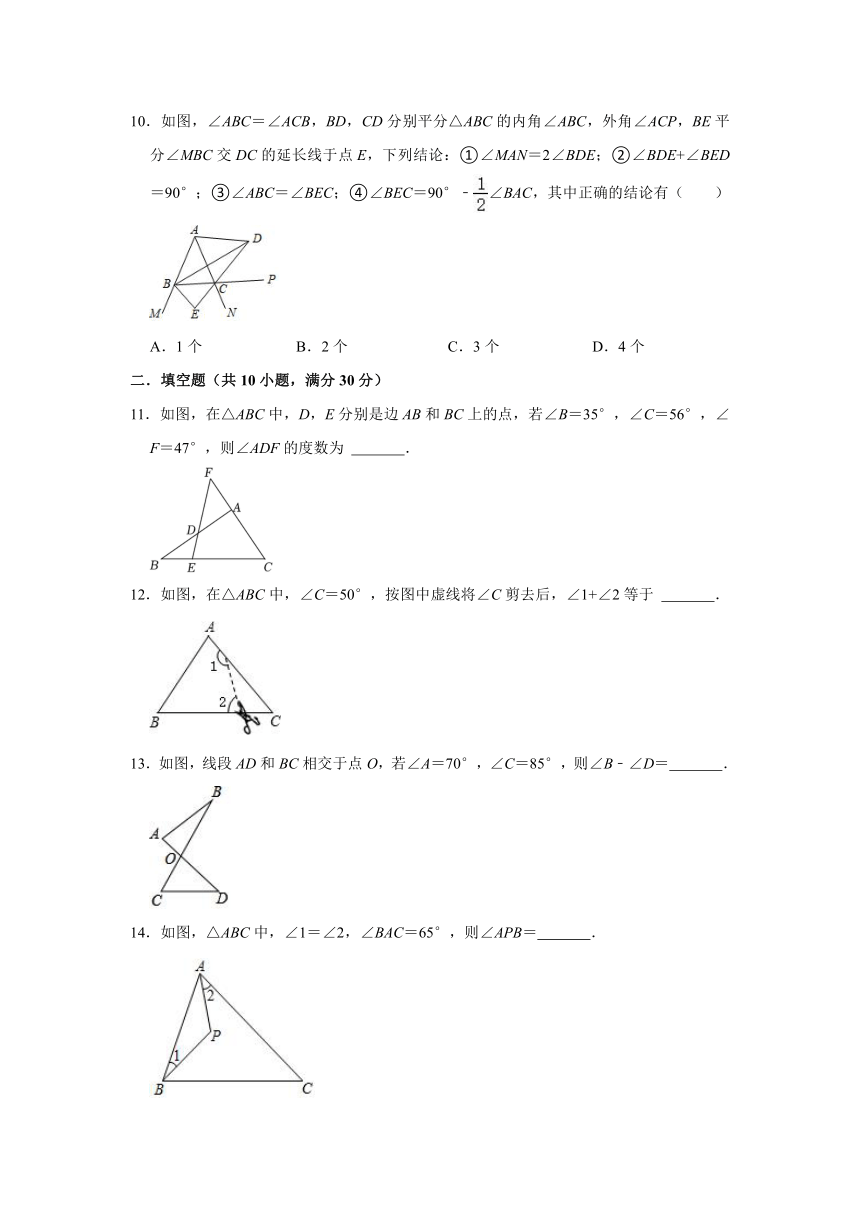
10.如图,∠ABC=∠ACB,BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,BE平分∠MBC交DC的延长线于点E,下列结论:①∠MAN=2∠BDE;②∠BDE+∠BED=90°;③∠ABC=∠BEC;④∠BEC=90°﹣∠BAC,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共10小题,满分30分)
11.如图,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 .
12.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .
13.如图,线段AD和BC相交于点O,若∠A=70°,∠C=85°,则∠B﹣∠D= .
14.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
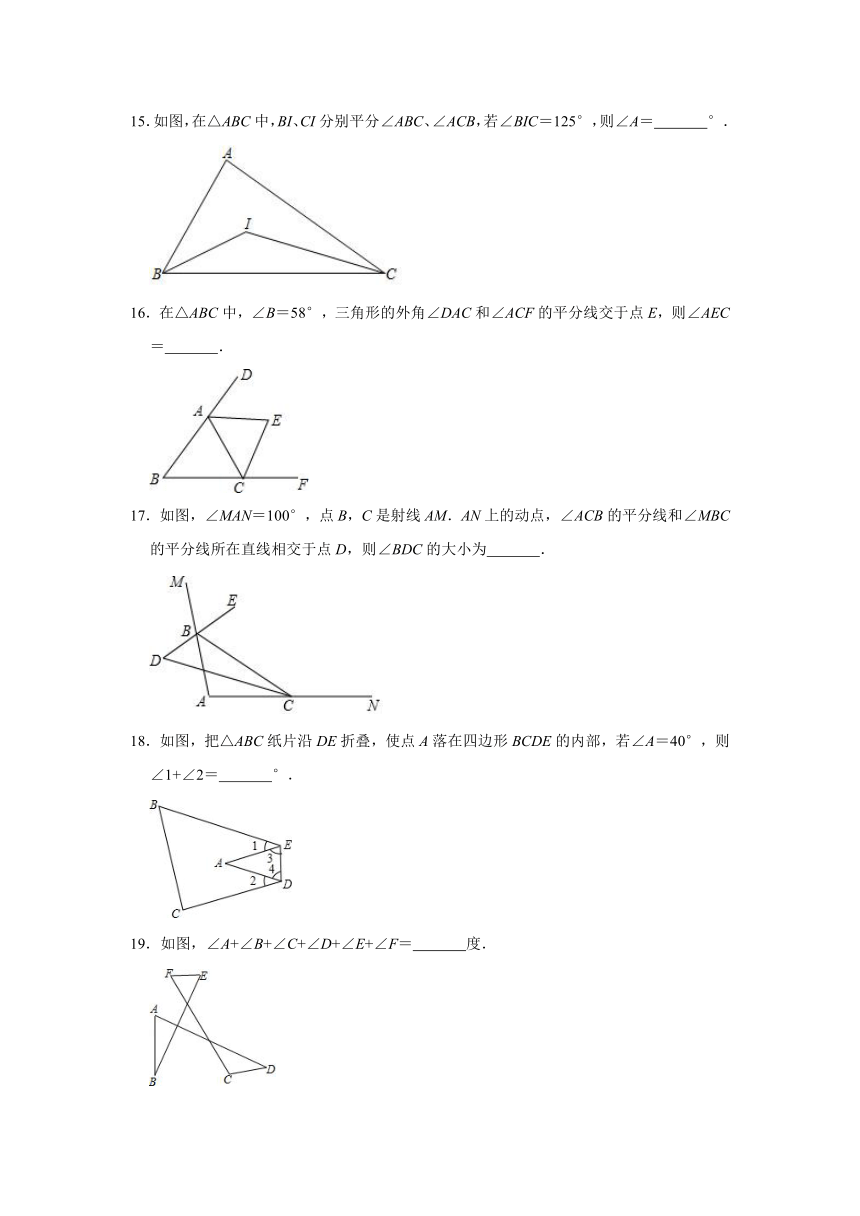
15.如图,在△ABC中,BI、CI分别平分∠ABC、∠ACB,若∠BIC=125°,则∠A= °.
16.在△ABC中,∠B=58°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
17.如图,∠MAN=100°,点B,C是射线AM.AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为 .
18.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,若∠A=40°,则∠1+∠2= °.
19.如图,∠A+∠B+∠C+∠D+∠E+∠F= 度.
20.如图,∠A+∠B+∠C+∠D+∠E的度数为 度.
三.解答题(共4小题,满分40分)
22.如图,在△ABC中,CD是∠ACB的角平分线交AC于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,求△CDE各内角的度数.
23.∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58°,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.
24.已知:在△ABC中,∠ABC、∠ACB的角平分线交于点O,∠ABC、∠ACB的外角平分线交于点D.
(1)请探究∠BOC的度数与∠BDC的度数有什么数量关系?并证明你的结论.
(2)若△ABC的三个外角平分线的交点为D、E、F,请判断△DEF是锐角三角形还是钝角三角形或直角三角形?并证明你的结论.
25.如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵∠B=45°,∠C的外角等于100°,
∴∠A=100°﹣45°=55°.
故选:B.
2.解:设三个角依次为2x,3x,5x,
则2x+3x+5x=180°,得x=18°,
所以最大的角为5x=90°,故选:C.
3.解:∵∠B=25°,∠1=70°,∠1=∠2,
∴∠CDA=∠2+∠B
=∠1+∠B
=70°+25°
=95°.
在△ACD中,∵∠ADC+∠A+∠C=180°,
∴∠C=180°﹣∠ADC﹣∠A
=180°﹣95°﹣35°
=50°.
故选:B.
4.解:延长AD交BC于点E,
∵∠AEC=∠A+∠B,∠1=∠C+∠ACE,
∴∠1=∠A+∠B+∠C,
故选:C.
5.解:A.∵∠2>∠D,∠1>∠2,
∴∠1>∠D,故本选项符合题意;
B.∠2>∠D,故本选项不符合题意;
C.∠1=∠2+∠A=∠D+∠3+∠A,∠2+∠3=∠D+∠3+∠3=2∠3+∠D,
又∵∠3和∠A不一定相等,
∴∠1和∠2+∠3不一定相等,故本选项不符合题意;
D.∠3和∠A不一定相等,故本选项不符合题意;
故选:A.
6.解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°.
故选:A.
7.解:如图,
由题意得:∠ABG=90°,
∵∠G=30°,
∴∠BFG=180°﹣∠ABG﹣∠G=60°,
∴∠AFH=∠BFG=60°,
∵∠α是△AFH的外角,∠A=45°,
∴∠α=∠A+∠AFH=105°,
故选:A.
8.解:∵∠ACD是△ABC三角形的外角,∠A1CD是△A1BC的外角,
∴∠A=∠ACD﹣∠ABC,∠A1=∠A1CD﹣∠A1BC,
∵BA1和CA1分别是∠ABC和∠ACD的角平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1=∠ACD﹣∠ABC=∠A=x°,
同理可得,∠A2=∠A1=×x°,∠A3=∠A2=××x°,…,
∴∠A2022=x°,
故选:C.
9.解:如图,假设m与AC和AB的交点分别是E、F,ED与AB的交点是G.
由外角定理可得:
∠1=∠AGE+∠A,∠AGE=∠D+∠2;
∴∠1=∠2+∠D+∠A=∠2+2∠A,
∴∠1﹣∠2=2∠A=60°.
故选:C.
10.解:∵BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,
∴∠ABD=∠CBD,∠ACD=∠PCD,
∴2∠PCD=2∠CBD+∠MAN,∠PCD=∠CBD+∠BDE,
由以上两式得∠MAN=2∠BDE,故①正确;
∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC,
∴∠DBE=∠DBC+∠EBC=∠ABC+∠MBC=×180°=90°,
∴∠BDE+∠BED=90°,
故②正确;
∵∠ABC=∠ACB,
∴∠CBM=∠NCB,
∵BE平分∠MBC,DE平分∠BCN,
∴∠EBC=∠ECB,
∴∠BEC=180°﹣2∠CBE
由∵∠ABC=180°﹣2∠CBE,
∴③∠ABC=∠BEC,故③正确;
∵∠BEC=180°﹣(∠MBC+∠NCB)=180°﹣(∠BAC+∠ACB+∠BAC+∠ABC)=180°﹣(180°+∠BAC),
∴∠BEC=90°﹣∠BAC,故④正确,
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵∠DAF是△ABC的外角,∠B=35°,∠C=56°,
∴∠DAF=∠B+∠C=91°,
∵∠F=47°,
∴∠ADF=180°﹣∠F﹣∠DAF=42°.
故答案为:42°.
12.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
13.解:∵∠C+∠D+∠COD=180°,∠A+∠B+∠AOB=180°,
∴∠D=180°﹣∠C﹣∠COD,∠B=180°﹣∠A﹣∠AOB.
∵∠AOB=∠COD,
∴∠B﹣∠D=(180°﹣∠A﹣∠AOB)﹣(180°﹣∠C﹣∠COD)=∠C﹣∠A=85°﹣70°=15°.
故答案为:15°.
14.解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
15.解:依题意,在△BIC中,125°+∠IBC+∠ICB=180°.
所以∠IBC+∠ICB=55°.
在△ABC中,∠A+∠ABC+∠ACB=180°.
又2∠IBC=∠ABC,2∠ICB=∠ACB,
所以∠A=180°﹣55°×2=70°.
故答案是:70°.
16.解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF,
∵∠DAC=∠B+∠2,∠ACF=∠B+∠1
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2),
∵∠B=58°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=119°
∴∠AEC=180°﹣(∠DAC+∠ACF)=61°.
故答案是:61°.
17.解:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故答案为:50°.
18.解:根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∠3+∠4=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A=80°.
故答案为:80°.
19.解:如右图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
20.解:延长CE交AB于F,
∵∠BFC是△ACF的外角,∴∠BFC=∠A+∠C,
∵∠EGB是△EDG的外角,∴∠EGB=∠D+∠DEG,
∵∠B+∠BFC+∠EGB=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
三.解答题(共4小题,满分40分)
22.解:∵CD是∠ACB的角平分线,
∴∠ACD=∠BCD=,
又∵∠BDC是△CDA的外角,
∴∠BDC=∠A+∠ACD,
∴∠ACD=∠BDC﹣∠A=80°﹣60°=20°,
∵DE∥BC,
∴∠CDE=∠BCD=20°,
∵∠CDE+∠DCE+∠DEC=180°,
∴∠DEC=180°﹣∠ECD﹣∠EDC
=180°﹣20°﹣20°
=140°,
∴∠CDE=∠ECD=20°,∠DEC=140°.
23.解:(1)∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2=∠ABC,∠4=∠ACD,
∴∠E=∠4﹣∠2=(∠ACD﹣∠ABC)=∠A=×58°=29°;
(2)∠A与∠E的关系是:∠E=∠A,
理由如下:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2=∠ABC,∠4=∠ACD,
∴∠E=∠4﹣∠2=(∠ACD﹣∠ABC)=∠A.
24.解:(1)∠BOC+∠BDC=180°,理由如下:
如图所示:
∵∠ABC、∠ACB的角平分线交于点O,
∴∠3=∠ABC,∠4=∠ACB,
∴∠BOC=180°﹣(∠3+∠4)=180°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣×(180°﹣∠A)=90°+∠A;
由题意得:∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,
∵∠ABC、∠ACB的外角平分线交于点D,
∴∠1=∠EBC=(∠A+∠ACB),
∠2=∠FCB=(∠A+∠ABC),
∴∠1+∠2=(∠A+∠ACB)+(∠A+∠ABC)=∠A+(∠ACB+∠ABC)=∠A+90°﹣∠A=90°+∠A,
∴∠BDC=180°﹣(∠1+∠2)=90°﹣∠A,
∴∠BOC+∠BDC=90°+∠A+90°﹣∠A=180°;
(2)△DEF是锐角三角形,理由如下:
如图所示:
由题意得:∠GBC=∠BAC+∠ACB,∠HCB=∠BAC+∠ABC,
∵∠ABC、∠ACB的外角平分线交于点D,
∴∠1=∠GBC=(∠BAC+∠ACB),
∠2=∠HCB=(∠BAC+∠ABC),
∴∠1+∠2=(∠BAC+∠ACB)+(∠BAC+∠ABC)=∠BAC+(∠ACB+∠ABC)=∠BAC+90°﹣∠BAC=90°+∠BAC,
∴∠D=180°﹣(∠1+∠2)=90°﹣∠BAC;
同理可得:∠E=90°﹣∠ABC,∠F=90°﹣∠ACB,
∴∠D,∠E,∠F都是锐角,
故△DEF是锐角三角形.
25.证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∴∠B+∠C=2∠P.
一.选择题(共10小题,满分30分)
1.在△ABC中,∠B=45°,∠C的外角等于100°,则∠A的度数是( )
A.65° B.55° C.54° D.35°
2.若一个三角形的三个内角度数的比为2:3:5,那么这个三角形的最大内角的度数为( )
A.54° B.60° C.90° D.100°
3.如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠1=70°,则∠C的大小为( )
A.40° B.50° C.75° D.85°
4.如图,下列关于∠A,∠B,∠C,∠1的关系中一定成立的是( )
A.∠A+∠B=∠C+∠1 B.∠A+∠1=∠B+∠C
C.∠A+∠B+∠C=∠1 D.∠A+∠B+∠C+∠1=360°
5.如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.则下列结论正确的是( )
A.∠1>∠D B.∠D>∠2 C.∠1=∠2+∠3 D.∠3=∠A
6.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线.∠BAC=50°,∠ABC=60°.则∠DAE+∠ACD等于( )
A.75° B.80° C.85° D.90°
7.如图所示,一副三角板叠放在一起,则图中∠α等于( )
A.105° B.115° C.120° D.135°
8.如图,在△ABC中,设∠A=x°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠A2021BC与∠A2021CD的平分线相交于点A2022,得∠A2022,则∠A2022是( )度.
A.x B.x C.x D.x
9.如图,在△ABC中,∠C=90°,∠A=30°,将△ABC沿直线m翻折,点A落在点D的位置,则∠1﹣∠2的度数是( )
A.30° B.45° C.60° D.75°
10.如图,∠ABC=∠ACB,BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,BE平分∠MBC交DC的延长线于点E,下列结论:①∠MAN=2∠BDE;②∠BDE+∠BED=90°;③∠ABC=∠BEC;④∠BEC=90°﹣∠BAC,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共10小题,满分30分)
11.如图,在△ABC中,D,E分别是边AB和BC上的点,若∠B=35°,∠C=56°,∠F=47°,则∠ADF的度数为 .
12.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .
13.如图,线段AD和BC相交于点O,若∠A=70°,∠C=85°,则∠B﹣∠D= .
14.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
15.如图,在△ABC中,BI、CI分别平分∠ABC、∠ACB,若∠BIC=125°,则∠A= °.
16.在△ABC中,∠B=58°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= .
17.如图,∠MAN=100°,点B,C是射线AM.AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为 .
18.如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,若∠A=40°,则∠1+∠2= °.
19.如图,∠A+∠B+∠C+∠D+∠E+∠F= 度.
20.如图,∠A+∠B+∠C+∠D+∠E的度数为 度.
三.解答题(共4小题,满分40分)
22.如图,在△ABC中,CD是∠ACB的角平分线交AC于点D,DE∥BC,交AC于点E,∠A=60°,∠BDC=80°,求△CDE各内角的度数.
23.∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58°,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.
24.已知:在△ABC中,∠ABC、∠ACB的角平分线交于点O,∠ABC、∠ACB的外角平分线交于点D.
(1)请探究∠BOC的度数与∠BDC的度数有什么数量关系?并证明你的结论.
(2)若△ABC的三个外角平分线的交点为D、E、F,请判断△DEF是锐角三角形还是钝角三角形或直角三角形?并证明你的结论.
25.如图1,已知线段AB、CD相交于点O,连接AC、BD.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,∠CAB与∠BDC的平分线AP、DP相交于点P,求证:∠B+∠C=2∠P.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵∠B=45°,∠C的外角等于100°,
∴∠A=100°﹣45°=55°.
故选:B.
2.解:设三个角依次为2x,3x,5x,
则2x+3x+5x=180°,得x=18°,
所以最大的角为5x=90°,故选:C.
3.解:∵∠B=25°,∠1=70°,∠1=∠2,
∴∠CDA=∠2+∠B
=∠1+∠B
=70°+25°
=95°.
在△ACD中,∵∠ADC+∠A+∠C=180°,
∴∠C=180°﹣∠ADC﹣∠A
=180°﹣95°﹣35°
=50°.
故选:B.
4.解:延长AD交BC于点E,
∵∠AEC=∠A+∠B,∠1=∠C+∠ACE,
∴∠1=∠A+∠B+∠C,
故选:C.
5.解:A.∵∠2>∠D,∠1>∠2,
∴∠1>∠D,故本选项符合题意;
B.∠2>∠D,故本选项不符合题意;
C.∠1=∠2+∠A=∠D+∠3+∠A,∠2+∠3=∠D+∠3+∠3=2∠3+∠D,
又∵∠3和∠A不一定相等,
∴∠1和∠2+∠3不一定相等,故本选项不符合题意;
D.∠3和∠A不一定相等,故本选项不符合题意;
故选:A.
6.解:∵AD是BC边上的高,∠ABC=60°,
∴∠BAD=30°,
∵∠BAC=50°,AE平分∠BAC,
∴∠BAE=25°,
∴∠DAE=30°﹣25°=5°,
∵△ABC中,∠C=180°﹣∠ABC﹣∠BAC=70°,
∴∠EAD+∠ACD=5°+70°=75°.
故选:A.
7.解:如图,
由题意得:∠ABG=90°,
∵∠G=30°,
∴∠BFG=180°﹣∠ABG﹣∠G=60°,
∴∠AFH=∠BFG=60°,
∵∠α是△AFH的外角,∠A=45°,
∴∠α=∠A+∠AFH=105°,
故选:A.
8.解:∵∠ACD是△ABC三角形的外角,∠A1CD是△A1BC的外角,
∴∠A=∠ACD﹣∠ABC,∠A1=∠A1CD﹣∠A1BC,
∵BA1和CA1分别是∠ABC和∠ACD的角平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1=∠ACD﹣∠ABC=∠A=x°,
同理可得,∠A2=∠A1=×x°,∠A3=∠A2=××x°,…,
∴∠A2022=x°,
故选:C.
9.解:如图,假设m与AC和AB的交点分别是E、F,ED与AB的交点是G.
由外角定理可得:
∠1=∠AGE+∠A,∠AGE=∠D+∠2;
∴∠1=∠2+∠D+∠A=∠2+2∠A,
∴∠1﹣∠2=2∠A=60°.
故选:C.
10.解:∵BD,CD分别平分△ABC的内角∠ABC,外角∠ACP,
∴∠ABD=∠CBD,∠ACD=∠PCD,
∴2∠PCD=2∠CBD+∠MAN,∠PCD=∠CBD+∠BDE,
由以上两式得∠MAN=2∠BDE,故①正确;
∵BD、BE分别平分△ABC的内角∠ABC、外角∠MBC,
∴∠DBE=∠DBC+∠EBC=∠ABC+∠MBC=×180°=90°,
∴∠BDE+∠BED=90°,
故②正确;
∵∠ABC=∠ACB,
∴∠CBM=∠NCB,
∵BE平分∠MBC,DE平分∠BCN,
∴∠EBC=∠ECB,
∴∠BEC=180°﹣2∠CBE
由∵∠ABC=180°﹣2∠CBE,
∴③∠ABC=∠BEC,故③正确;
∵∠BEC=180°﹣(∠MBC+∠NCB)=180°﹣(∠BAC+∠ACB+∠BAC+∠ABC)=180°﹣(180°+∠BAC),
∴∠BEC=90°﹣∠BAC,故④正确,
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵∠DAF是△ABC的外角,∠B=35°,∠C=56°,
∴∠DAF=∠B+∠C=91°,
∵∠F=47°,
∴∠ADF=180°﹣∠F﹣∠DAF=42°.
故答案为:42°.
12.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
13.解:∵∠C+∠D+∠COD=180°,∠A+∠B+∠AOB=180°,
∴∠D=180°﹣∠C﹣∠COD,∠B=180°﹣∠A﹣∠AOB.
∵∠AOB=∠COD,
∴∠B﹣∠D=(180°﹣∠A﹣∠AOB)﹣(180°﹣∠C﹣∠COD)=∠C﹣∠A=85°﹣70°=15°.
故答案为:15°.
14.解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
15.解:依题意,在△BIC中,125°+∠IBC+∠ICB=180°.
所以∠IBC+∠ICB=55°.
在△ABC中,∠A+∠ABC+∠ACB=180°.
又2∠IBC=∠ABC,2∠ICB=∠ACB,
所以∠A=180°﹣55°×2=70°.
故答案是:70°.
16.解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF,
∵∠DAC=∠B+∠2,∠ACF=∠B+∠1
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2),
∵∠B=58°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=119°
∴∠AEC=180°﹣(∠DAC+∠ACF)=61°.
故答案是:61°.
17.解:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故答案为:50°.
18.解:根据平角的定义和折叠的性质,得
∠1+∠2=360°﹣2(∠3+∠4).
又∠3+∠4=180°﹣∠A,
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A=80°.
故答案为:80°.
19.解:如右图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
20.解:延长CE交AB于F,
∵∠BFC是△ACF的外角,∴∠BFC=∠A+∠C,
∵∠EGB是△EDG的外角,∴∠EGB=∠D+∠DEG,
∵∠B+∠BFC+∠EGB=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:如图连接CE,
根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3,
在△DCE中有,∠D+∠2+∠DCB+∠3+∠AED=180°,
∴∠D+∠A+∠DCB+∠B+∠AED=180°.
三.解答题(共4小题,满分40分)
22.解:∵CD是∠ACB的角平分线,
∴∠ACD=∠BCD=,
又∵∠BDC是△CDA的外角,
∴∠BDC=∠A+∠ACD,
∴∠ACD=∠BDC﹣∠A=80°﹣60°=20°,
∵DE∥BC,
∴∠CDE=∠BCD=20°,
∵∠CDE+∠DCE+∠DEC=180°,
∴∠DEC=180°﹣∠ECD﹣∠EDC
=180°﹣20°﹣20°
=140°,
∴∠CDE=∠ECD=20°,∠DEC=140°.
23.解:(1)∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2=∠ABC,∠4=∠ACD,
∴∠E=∠4﹣∠2=(∠ACD﹣∠ABC)=∠A=×58°=29°;
(2)∠A与∠E的关系是:∠E=∠A,
理由如下:∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC,
∴∠A=∠ACD﹣∠ABC,
∵BE平分∠ABC,CE平分∠ACD,
∴∠2=∠ABC,∠4=∠ACD,
∴∠E=∠4﹣∠2=(∠ACD﹣∠ABC)=∠A.
24.解:(1)∠BOC+∠BDC=180°,理由如下:
如图所示:
∵∠ABC、∠ACB的角平分线交于点O,
∴∠3=∠ABC,∠4=∠ACB,
∴∠BOC=180°﹣(∠3+∠4)=180°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣×(180°﹣∠A)=90°+∠A;
由题意得:∠EBC=∠A+∠ACB,∠FCB=∠A+∠ABC,
∵∠ABC、∠ACB的外角平分线交于点D,
∴∠1=∠EBC=(∠A+∠ACB),
∠2=∠FCB=(∠A+∠ABC),
∴∠1+∠2=(∠A+∠ACB)+(∠A+∠ABC)=∠A+(∠ACB+∠ABC)=∠A+90°﹣∠A=90°+∠A,
∴∠BDC=180°﹣(∠1+∠2)=90°﹣∠A,
∴∠BOC+∠BDC=90°+∠A+90°﹣∠A=180°;
(2)△DEF是锐角三角形,理由如下:
如图所示:
由题意得:∠GBC=∠BAC+∠ACB,∠HCB=∠BAC+∠ABC,
∵∠ABC、∠ACB的外角平分线交于点D,
∴∠1=∠GBC=(∠BAC+∠ACB),
∠2=∠HCB=(∠BAC+∠ABC),
∴∠1+∠2=(∠BAC+∠ACB)+(∠BAC+∠ABC)=∠BAC+(∠ACB+∠ABC)=∠BAC+90°﹣∠BAC=90°+∠BAC,
∴∠D=180°﹣(∠1+∠2)=90°﹣∠BAC;
同理可得:∠E=90°﹣∠ABC,∠F=90°﹣∠ACB,
∴∠D,∠E,∠F都是锐角,
故△DEF是锐角三角形.
25.证明:(1)在△AOC中,∠A+∠C=180°﹣∠AOC,
在△BOD中,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)在AP、CD相交线中,有∠CAP+∠C=∠P+∠CDP,
在AB、DP相交线中,有∠B+∠BDP=∠P+∠BAP,
∴∠B+∠C+∠CAP+∠BDP=2∠P+∠CDP+∠BAP,
∵AP、DP分别平分∠CAB、∠BDC,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∴∠B+∠C=2∠P.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
