2022-2023学年青岛版七年级数学上册2.1 有理数 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年青岛版七年级数学上册2.1 有理数 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 16:01:43 | ||
图片预览








文档简介
(共22张PPT)
2.1 有理数
青岛版 数学 七年级(上) 第2章 有理数
情景导入
在小学时我们已经学习过负数,你能说出下面实例中这些带有“+”或“-”的意义吗?
(1)某家用电冰箱的说明书上写着:冰箱冷藏室的温度为+2℃,冷冻室的温度为-18℃。
零上2℃和零下18℃
(2)上海市2010年户籍人口出生率为+7.13‰,自然增长率为-0.60‰。
增长7.13‰和减少0.60‰
(3)北京与东京的时差(单位:时)+1,与巴黎的时差为-7.
早1小时和晚7小时
观察上面的三组数据,它们有什么样的共同点?
为了区别具有相反意义的两个量,我们把其中一种意义的量规定为正的,把与它相反意义的量规定为负的。
1、在下列横线上填上适当的词,使前后构成意义相反的量:
(1)收入1300元, 800元;
(2) 80米,下降64米;
(3)向北走30米, 50米.
(4)把公元2020年记作+2020年,那么-20年
表示 _______。
支出
上升
向南走
公元前20年
例题讲解
(5)如果将+8元计为收入8元,则-6元表示 _____ 。
(6)高出海平面789米计为+789米,
则-789米表示_______ _____。
(7)减少60千克计为-60千克,则+80千克
表示 __________。
支出6元
低于海平面789米
增加80千克
2、用正负数填空:
(1)如果零上5°C记作+5°C,那么零下3°C
记作______;
(2)如果向西运动4米表示- 4米,那么向东运动2米
表示_____,原地不动记为_______.
(3)某仓库运进面粉7.5吨记作+7.5吨, 那么运出
3.8吨应记作______.
0表示没有吗
-3°C
+2米
0米
-3.8吨
例题讲解
1、正数和负数的意义:
正数与负数通常用来表示具有相反意义的量。
课内小结1
注意:
(1)0既不是正数,也不是负数;
(2)0不单单表示没有;
(3)“+”号可以省略。
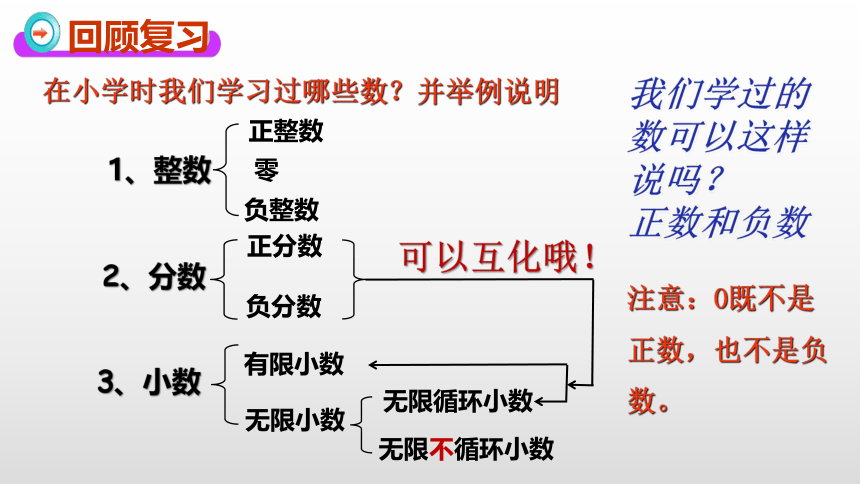
在小学时我们学习过哪些数?并举例说明
回顾复习
1、整数
正整数
零
负整数
2、分数
正分数
负分数
3、小数
有限小数
无限小数
无限循环小数
无限不循环小数
可以互化哦!
我们学过的
数可以这样
说吗?
正数和负数
注意:0既不是正数,也不是负数。
下列各数中,哪些是正整数?哪些是负整数 哪些是整数?
哪些是正分数?哪些是负分数?哪些是分数?
新知探索2
正整数、零、负整数统称整数。
正分数、负分数统称分数。
整数和分数统称有理数。
2、有理数的定义:
课内小结2
3、有理数的分类:
正整数
负整数
0
整数
正分数
负分数
分数
有理数
注意:我们把有限小数,无限循环小数和百分数都看作分数。
①按定义分类:
问题:小数是分数吗?
不是所有的小数都是分数。
圆周率π是一个无限不循环小数,它就不能化成分数。
讨论思考
(1)正数有:__________________________;
(2)负数有:__________________________;
(3)正整数有:_____;(4)正分数有:_________;
(5)负整数有:_____;(6)负分数有:_________ .
把下列各数填入相应集合:
新知探索3
你是否发现了有理数的另一种新的分类方法
0怎么办呢?
正数和正有理数有什么区别呢?
正整数
正分数
正有理数
负有理数
负整数
负分数
有理数
0
②按性质分类:
注意:正数和正有理数是不同的,例如: 就是正数,但不是正有理数;
课内小结3
3、有理数的分类:
3、把下列各数填在相应的括号中:
正数:{ };
负数:{ };
分数:{ };
整数:{ };
非负数:{ };
有理数:{ };
例题讲解
4、下列说法正确的是( )
A.非负有理数就是正有理数
B. 0仅表示没有,是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数
D
5、最小的正整数是___,最大的负整数是_____,所有大于-4的负整数有_________,不大于3的非负整数有_________。
1
-1
-1,-2,-3
0,1,2,3
例题讲解
例题讲解
6、下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数;
A.①② B.②③ C.③④ D.①④
C
7、(1)既是分数又是负数的数是_______;
(2)既是非负数又是整数的数是_______;
(3)非负整数又称为________;
(4)非负数包括________和_______;
(5)非正数包括________和_______.
非负整数
负分数
自然数
正数
0
负数
0
9、观察下列各组数,请找出它们的规律,并在横线上填上相应的数字.
6
8
1
0
-1
0
14
-16
8、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
例题讲解
课堂练习
P30 练习1、2
课堂总结
1、正数和负数的意义:
2、有理数的定义:
3、有理数的分类:
①按定义分类:
②按性质分类:
进步往往从归纳反思开始!
课下作业
P30 习题2.1 1~9题
同学们,下课!
2.1 有理数
青岛版 数学 七年级(上) 第2章 有理数
情景导入
在小学时我们已经学习过负数,你能说出下面实例中这些带有“+”或“-”的意义吗?
(1)某家用电冰箱的说明书上写着:冰箱冷藏室的温度为+2℃,冷冻室的温度为-18℃。
零上2℃和零下18℃
(2)上海市2010年户籍人口出生率为+7.13‰,自然增长率为-0.60‰。
增长7.13‰和减少0.60‰
(3)北京与东京的时差(单位:时)+1,与巴黎的时差为-7.
早1小时和晚7小时
观察上面的三组数据,它们有什么样的共同点?
为了区别具有相反意义的两个量,我们把其中一种意义的量规定为正的,把与它相反意义的量规定为负的。
1、在下列横线上填上适当的词,使前后构成意义相反的量:
(1)收入1300元, 800元;
(2) 80米,下降64米;
(3)向北走30米, 50米.
(4)把公元2020年记作+2020年,那么-20年
表示 _______。
支出
上升
向南走
公元前20年
例题讲解
(5)如果将+8元计为收入8元,则-6元表示 _____ 。
(6)高出海平面789米计为+789米,
则-789米表示_______ _____。
(7)减少60千克计为-60千克,则+80千克
表示 __________。
支出6元
低于海平面789米
增加80千克
2、用正负数填空:
(1)如果零上5°C记作+5°C,那么零下3°C
记作______;
(2)如果向西运动4米表示- 4米,那么向东运动2米
表示_____,原地不动记为_______.
(3)某仓库运进面粉7.5吨记作+7.5吨, 那么运出
3.8吨应记作______.
0表示没有吗
-3°C
+2米
0米
-3.8吨
例题讲解
1、正数和负数的意义:
正数与负数通常用来表示具有相反意义的量。
课内小结1
注意:
(1)0既不是正数,也不是负数;
(2)0不单单表示没有;
(3)“+”号可以省略。
在小学时我们学习过哪些数?并举例说明
回顾复习
1、整数
正整数
零
负整数
2、分数
正分数
负分数
3、小数
有限小数
无限小数
无限循环小数
无限不循环小数
可以互化哦!
我们学过的
数可以这样
说吗?
正数和负数
注意:0既不是正数,也不是负数。
下列各数中,哪些是正整数?哪些是负整数 哪些是整数?
哪些是正分数?哪些是负分数?哪些是分数?
新知探索2
正整数、零、负整数统称整数。
正分数、负分数统称分数。
整数和分数统称有理数。
2、有理数的定义:
课内小结2
3、有理数的分类:
正整数
负整数
0
整数
正分数
负分数
分数
有理数
注意:我们把有限小数,无限循环小数和百分数都看作分数。
①按定义分类:
问题:小数是分数吗?
不是所有的小数都是分数。
圆周率π是一个无限不循环小数,它就不能化成分数。
讨论思考
(1)正数有:__________________________;
(2)负数有:__________________________;
(3)正整数有:_____;(4)正分数有:_________;
(5)负整数有:_____;(6)负分数有:_________ .
把下列各数填入相应集合:
新知探索3
你是否发现了有理数的另一种新的分类方法
0怎么办呢?
正数和正有理数有什么区别呢?
正整数
正分数
正有理数
负有理数
负整数
负分数
有理数
0
②按性质分类:
注意:正数和正有理数是不同的,例如: 就是正数,但不是正有理数;
课内小结3
3、有理数的分类:
3、把下列各数填在相应的括号中:
正数:{ };
负数:{ };
分数:{ };
整数:{ };
非负数:{ };
有理数:{ };
例题讲解
4、下列说法正确的是( )
A.非负有理数就是正有理数
B. 0仅表示没有,是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数
D
5、最小的正整数是___,最大的负整数是_____,所有大于-4的负整数有_________,不大于3的非负整数有_________。
1
-1
-1,-2,-3
0,1,2,3
例题讲解
例题讲解
6、下列说法正确的是( )
①1是最小的正有理数; ②-1是最大的负有理数;
③0是最小的非负有理数;④0是最大的非正有理数;
A.①② B.②③ C.③④ D.①④
C
7、(1)既是分数又是负数的数是_______;
(2)既是非负数又是整数的数是_______;
(3)非负整数又称为________;
(4)非负数包括________和_______;
(5)非正数包括________和_______.
非负整数
负分数
自然数
正数
0
负数
0
9、观察下列各组数,请找出它们的规律,并在横线上填上相应的数字.
6
8
1
0
-1
0
14
-16
8、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
例题讲解
课堂练习
P30 练习1、2
课堂总结
1、正数和负数的意义:
2、有理数的定义:
3、有理数的分类:
①按定义分类:
②按性质分类:
进步往往从归纳反思开始!
课下作业
P30 习题2.1 1~9题
同学们,下课!
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
