2022-2023学年安徽省滁州市定远县启明中学九年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 2022-2023学年安徽省滁州市定远县启明中学九年级(上)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 17:03:43 | ||
图片预览


文档简介
2022-2023学年安徽省滁州市定远县启明中学九年级(上)期末数学试卷
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 关于的函数是二次函数的条件是( )
A. B. C. D.
2. 若点是线段的黄金分割点,,则的长为( )
A. B. C. D.
3. 在中,,,,下列各式中,正确的是( )
A. B. C. D.
4. 如图,是 的边的延长线上的一点,连接,交边于点若,则与的周长之比为( )
A. B. C. D.
5. 如图,,和平分和,过点且与直线垂直.若,则点到的距离是( )
A.
B.
C.
D.
6. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( )
A.
B.
C.
D.
7. 如图,矩形的边与轴平行,顶点的坐标为,的坐标为,反比例函数的图象与矩形有公共点,则的取值范围为( )
A. B. C. D.
8. 如图,在边长为的小正方形网格中,点,,,都在这些小正方形的顶点上,,相交于点,则( )
A. B. C. D.
9. 如图,在中,、为边的三等分点,,为与的交点若,则( )
A.
B.
C.
D.
10. 平面直角坐标系中,随着取值的变化,一次函数与函数的图象的公共点的个数分别为( )
A. ,, B. ,,,
C. ,,,, D. ,,
二、填空题(本大题共4小题,共20分)
11. 反比例函数的图象的一个分支在第二象限,则的取值范围是 .
12. 在中,若,,都是锐角,则的度数是 .
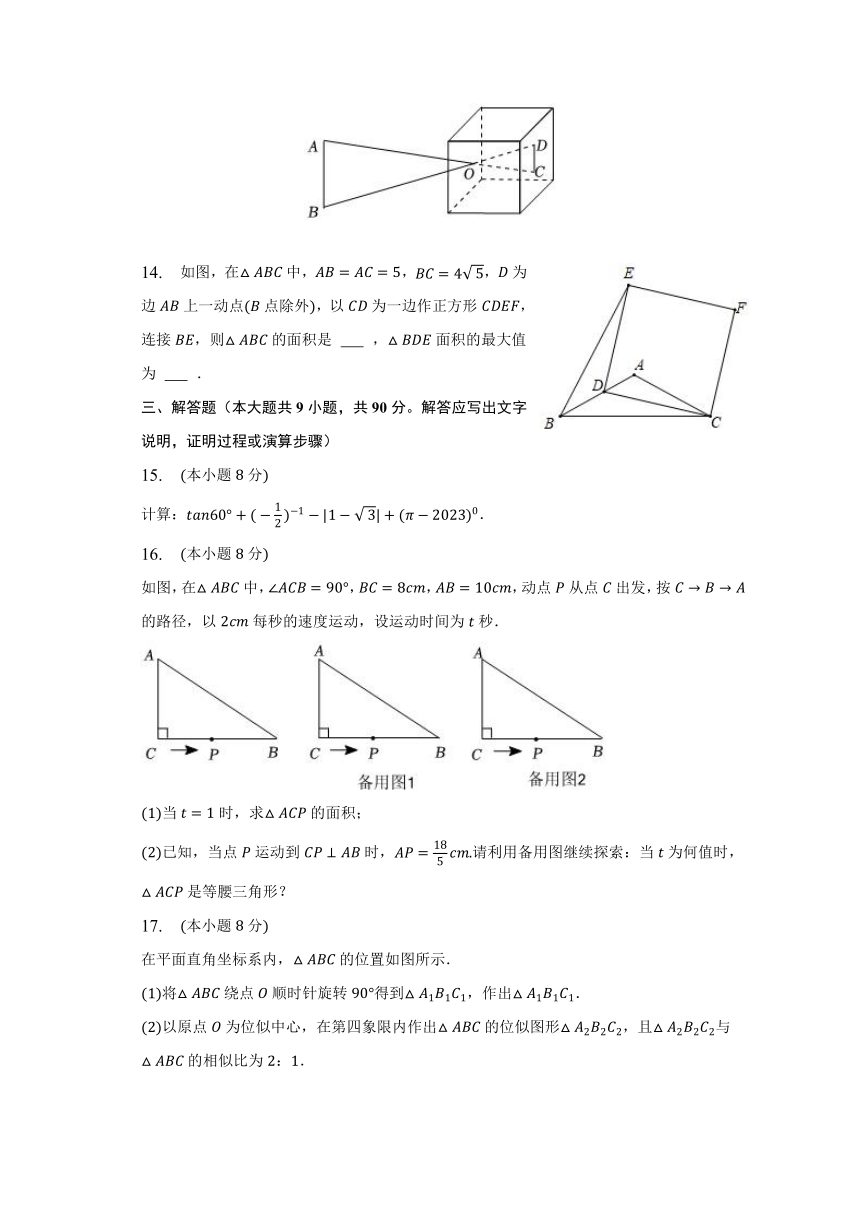
13. 如图是小孔成像原理的示意图,,,若物体的高度为,则像的高度是 .
14. 如图,在中,,,为边上一动点点除外,以为一边作正方形,连接,则的面积是 ,面积的最大值为 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
计算:.
16. 本小题分
如图,在中,,,,动点从点出发,按的路径,以每秒的速度运动,设运动时间为秒.
当时,求的面积;
已知,当点运动到时,请利用备用图继续探索:当为何值时,是等腰三角形?
17. 本小题分
在平面直角坐标系内,的位置如图所示.
将绕点顺时针旋转得到,作出.
以原点为位似中心,在第四象限内作出的位似图形,且与的相似比为:.
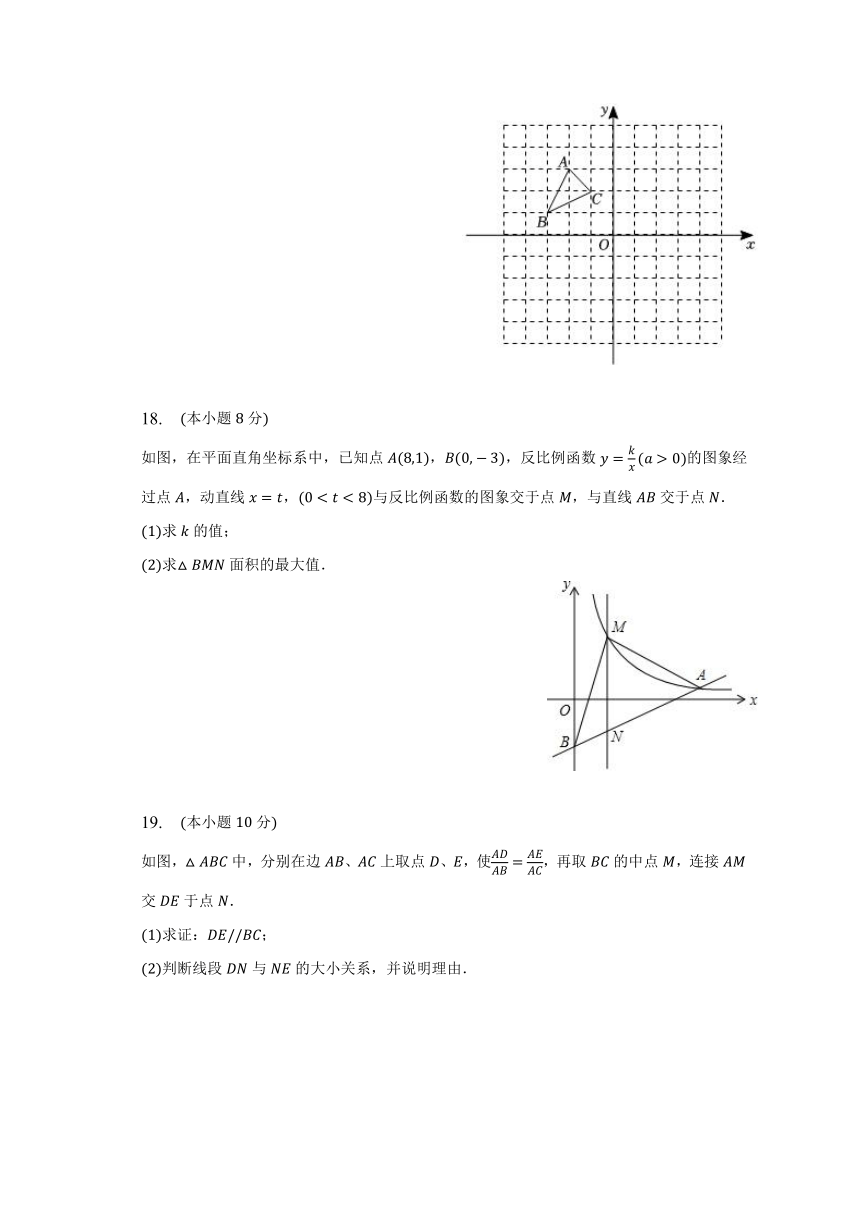
18. 本小题分
如图,在平面直角坐标系中,已知点,,反比例函数的图象经过点,动直线,与反比例函数的图象交于点,与直线交于点.
求的值;
求面积的最大值.
19. 本小题分
如图,中,分别在边、上取点、,使,再取的中点,连接交于点.
求证:;
判断线段与的大小关系,并说明理由.
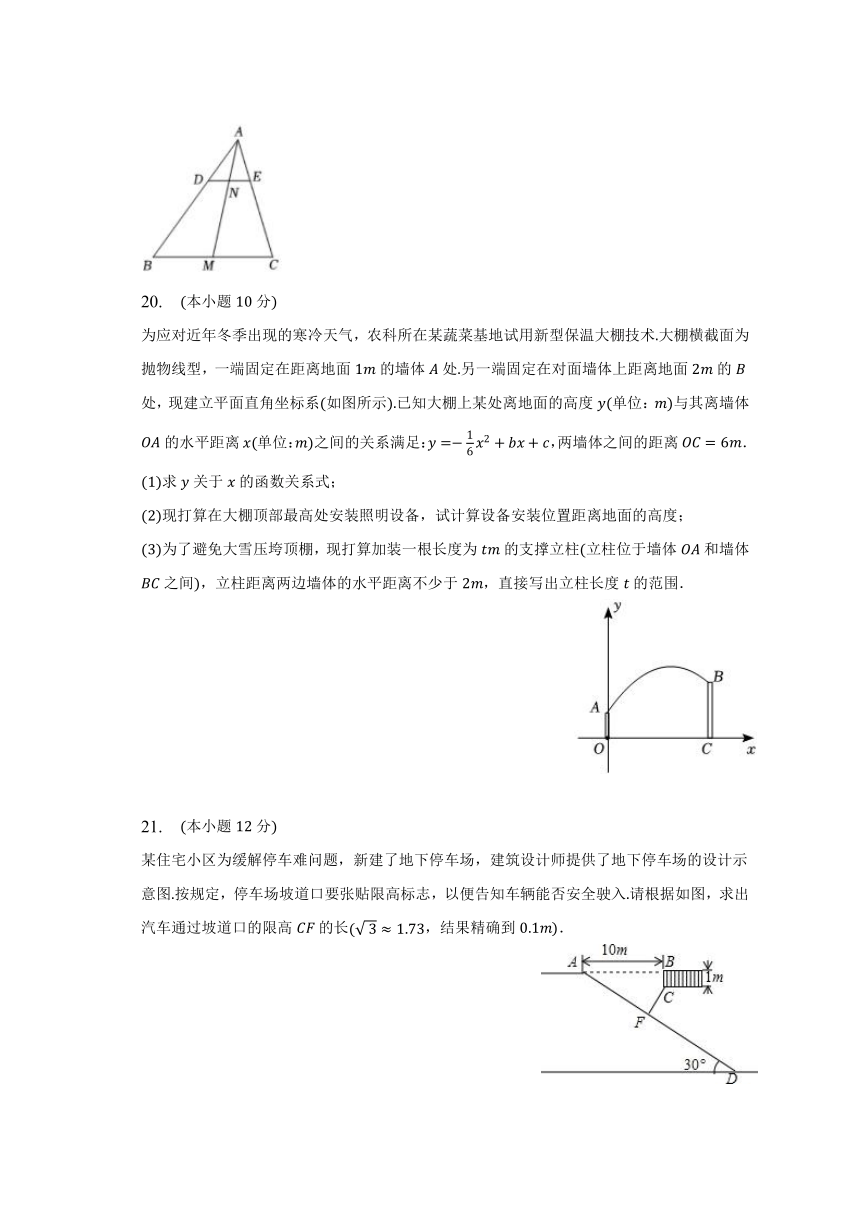
20. 本小题分
为应对近年冬季出现的寒冷天气,农科所在某蔬菜基地试用新型保温大棚技术大棚横截面为抛物线型,一端固定在距离地面的墙体处另一端固定在对面墙体上距离地面的处,现建立平面直角坐标系如图所示已知大棚上某处离地面的高度单位:与其离墙体的水平距离单位:之间的关系满足:,两墙体之间的距离.
求关于的函数关系式;
现打算在大棚顶部最高处安装照明设备,试计算设备安装位置距离地面的高度;
为了避免大雪压垮顶棚,现打算加装一根长度为的支撑立柱立柱位于墙体和墙体之间,立柱距离两边墙体的水平距离不少于,直接写出立柱长度的范围.
21. 本小题分
某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入请根据如图,求出汽车通过坡道口的限高的长,结果精确到.
22. 本小题分
现要修建一条公路隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以为坐标原点,以所在直线为轴,以过点垂直于轴的直线为轴,建立平面直角坐标系根据设计要求,隧道上距点水平方向米及竖直方向米的点有一照明灯.
求满足设计要求的抛物线的函数表达式;
现需在这个隧道中间位置设置双向通行车道,加中间隔离带合计宽度米,隧道入口对车辆要求限高,请通过计算说明高度不超过米的车辆能否安全通过该隧道?
23. 本小题分
如图,在等腰中,,,点在线段的中垂线上,连接、.
如图,若时,连接并延长交于点,若,求的面积;
如图,连接,若,过点作于点,交于点,过点作交的延长线于点求证:;
在等腰内部有一点,连接、、,将沿直线翻折至所在平面内得到,连接,当取得最小值时,请直接写出的值.
答 案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.
13.
14.
15.解:原式
.
16.解:在中,,
,,
,
如图,时,,
所以的面积;
如图,,,:
因为是以为边的等腰三角形,
如图,当时,;
如图,当时,;
如图中,当时,过点作于点.
,,
,
,
;
如图,当时,,,
,,
,
,
,
.
综上所述,或或或.
17.解:如图,即为所作.
如图,即为所作.
18.解:把点代入反比例函数得:
,,
;
设直线的解析式为:,
根据题意得:,
解得:,,
直线的解析式为:;
设,,
则,
的面积,
的面积是的二次函数,
,
有最大值,
当时,的面积的最大值为.
19.证明:,
∽
,
;
解:结论:.
理由:,
,
,
,
是的中点,
,
.
20.解:由题意可得,,,
将,代入得,
,
解得:,
;
,
顶点坐标为,
,图象开口向下,
函数有最大值,
设备安装位置距离地面的高度为;
立柱距离两边墙体的水平距离不少于,
当时,,
当时,,
,
.
21.解:如图,延长交于点,在中,,,
,
米,
在中,,米,
使用的方法是“去尾法”,
答:坡道口的限高的长是.
22.解:抛物线经过点,,
可以设抛物线的解析式为,
把点代入,可得,
抛物线的解析式为
即;
解:,
根据对称性,令,得
,
高度不超过米的车辆能安全通过该隧道.
23.解:如图,过作,交于,
点在的中垂线上,
,
,
,
,
,
,
,
,
;
证明:在线段上截取,过点作,交于,如图:
,,,
,,
,,,
,
,
,
,
,即,
在和中,
,
≌,
,
在和中,
,
≌,
,,,
在的中垂线上,
,
,
,
,
四边形是矩形,
,,
,
,
,
,
,
,
在和中,
,
≌,
,
,
,
,
,
;
解:如图,过作,使,作,使,
,
,
,
,
,
,
∽,
,
,
如图,当、、、在一条直线上时,的值最小,即的值最小,
如图,过作,交于,过作交的延长线于,过作,交的延长线于,
,
,
,
,
设,则,
,
,
,
,
∽,
,
,
,
∽,
,
,,
,
,
,
,
,
,
在和中,
,
≌,
,
由翻折得:,,
,
,
,
∽,
,
设,则,
,
,
解得:,
,
,
,
.
一、选择题(本大题共10小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 关于的函数是二次函数的条件是( )
A. B. C. D.
2. 若点是线段的黄金分割点,,则的长为( )
A. B. C. D.
3. 在中,,,,下列各式中,正确的是( )
A. B. C. D.
4. 如图,是 的边的延长线上的一点,连接,交边于点若,则与的周长之比为( )
A. B. C. D.
5. 如图,,和平分和,过点且与直线垂直.若,则点到的距离是( )
A.
B.
C.
D.
6. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( )
A.
B.
C.
D.
7. 如图,矩形的边与轴平行,顶点的坐标为,的坐标为,反比例函数的图象与矩形有公共点,则的取值范围为( )
A. B. C. D.
8. 如图,在边长为的小正方形网格中,点,,,都在这些小正方形的顶点上,,相交于点,则( )
A. B. C. D.
9. 如图,在中,、为边的三等分点,,为与的交点若,则( )
A.
B.
C.
D.
10. 平面直角坐标系中,随着取值的变化,一次函数与函数的图象的公共点的个数分别为( )
A. ,, B. ,,,
C. ,,,, D. ,,
二、填空题(本大题共4小题,共20分)
11. 反比例函数的图象的一个分支在第二象限,则的取值范围是 .
12. 在中,若,,都是锐角,则的度数是 .
13. 如图是小孔成像原理的示意图,,,若物体的高度为,则像的高度是 .
14. 如图,在中,,,为边上一动点点除外,以为一边作正方形,连接,则的面积是 ,面积的最大值为 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 本小题分
计算:.
16. 本小题分
如图,在中,,,,动点从点出发,按的路径,以每秒的速度运动,设运动时间为秒.
当时,求的面积;
已知,当点运动到时,请利用备用图继续探索:当为何值时,是等腰三角形?
17. 本小题分
在平面直角坐标系内,的位置如图所示.
将绕点顺时针旋转得到,作出.
以原点为位似中心,在第四象限内作出的位似图形,且与的相似比为:.
18. 本小题分
如图,在平面直角坐标系中,已知点,,反比例函数的图象经过点,动直线,与反比例函数的图象交于点,与直线交于点.
求的值;
求面积的最大值.
19. 本小题分
如图,中,分别在边、上取点、,使,再取的中点,连接交于点.
求证:;
判断线段与的大小关系,并说明理由.
20. 本小题分
为应对近年冬季出现的寒冷天气,农科所在某蔬菜基地试用新型保温大棚技术大棚横截面为抛物线型,一端固定在距离地面的墙体处另一端固定在对面墙体上距离地面的处,现建立平面直角坐标系如图所示已知大棚上某处离地面的高度单位:与其离墙体的水平距离单位:之间的关系满足:,两墙体之间的距离.
求关于的函数关系式;
现打算在大棚顶部最高处安装照明设备,试计算设备安装位置距离地面的高度;
为了避免大雪压垮顶棚,现打算加装一根长度为的支撑立柱立柱位于墙体和墙体之间,立柱距离两边墙体的水平距离不少于,直接写出立柱长度的范围.
21. 本小题分
某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入请根据如图,求出汽车通过坡道口的限高的长,结果精确到.
22. 本小题分
现要修建一条公路隧道,其截面为抛物线型,如图所示,线段表示水平的路面,以为坐标原点,以所在直线为轴,以过点垂直于轴的直线为轴,建立平面直角坐标系根据设计要求,隧道上距点水平方向米及竖直方向米的点有一照明灯.
求满足设计要求的抛物线的函数表达式;
现需在这个隧道中间位置设置双向通行车道,加中间隔离带合计宽度米,隧道入口对车辆要求限高,请通过计算说明高度不超过米的车辆能否安全通过该隧道?
23. 本小题分
如图,在等腰中,,,点在线段的中垂线上,连接、.
如图,若时,连接并延长交于点,若,求的面积;
如图,连接,若,过点作于点,交于点,过点作交的延长线于点求证:;
在等腰内部有一点,连接、、,将沿直线翻折至所在平面内得到,连接,当取得最小值时,请直接写出的值.
答 案
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.
13.
14.
15.解:原式
.
16.解:在中,,
,,
,
如图,时,,
所以的面积;
如图,,,:
因为是以为边的等腰三角形,
如图,当时,;
如图,当时,;
如图中,当时,过点作于点.
,,
,
,
;
如图,当时,,,
,,
,
,
,
.
综上所述,或或或.
17.解:如图,即为所作.
如图,即为所作.
18.解:把点代入反比例函数得:
,,
;
设直线的解析式为:,
根据题意得:,
解得:,,
直线的解析式为:;
设,,
则,
的面积,
的面积是的二次函数,
,
有最大值,
当时,的面积的最大值为.
19.证明:,
∽
,
;
解:结论:.
理由:,
,
,
,
是的中点,
,
.
20.解:由题意可得,,,
将,代入得,
,
解得:,
;
,
顶点坐标为,
,图象开口向下,
函数有最大值,
设备安装位置距离地面的高度为;
立柱距离两边墙体的水平距离不少于,
当时,,
当时,,
,
.
21.解:如图,延长交于点,在中,,,
,
米,
在中,,米,
使用的方法是“去尾法”,
答:坡道口的限高的长是.
22.解:抛物线经过点,,
可以设抛物线的解析式为,
把点代入,可得,
抛物线的解析式为
即;
解:,
根据对称性,令,得
,
高度不超过米的车辆能安全通过该隧道.
23.解:如图,过作,交于,
点在的中垂线上,
,
,
,
,
,
,
,
,
;
证明:在线段上截取,过点作,交于,如图:
,,,
,,
,,,
,
,
,
,
,即,
在和中,
,
≌,
,
在和中,
,
≌,
,,,
在的中垂线上,
,
,
,
,
四边形是矩形,
,,
,
,
,
,
,
,
在和中,
,
≌,
,
,
,
,
,
;
解:如图,过作,使,作,使,
,
,
,
,
,
,
∽,
,
,
如图,当、、、在一条直线上时,的值最小,即的值最小,
如图,过作,交于,过作交的延长线于,过作,交的延长线于,
,
,
,
,
设,则,
,
,
,
,
∽,
,
,
,
∽,
,
,,
,
,
,
,
,
,
在和中,
,
≌,
,
由翻折得:,,
,
,
,
∽,
,
设,则,
,
,
解得:,
,
,
,
.
同课章节目录
