八年级数学上册试题 3.2 平面直角坐标系--面积问题专项练习-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 3.2 平面直角坐标系--面积问题专项练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 23:16:48 | ||
图片预览


文档简介
3.2 平面直角坐标系--面积问题专项练习
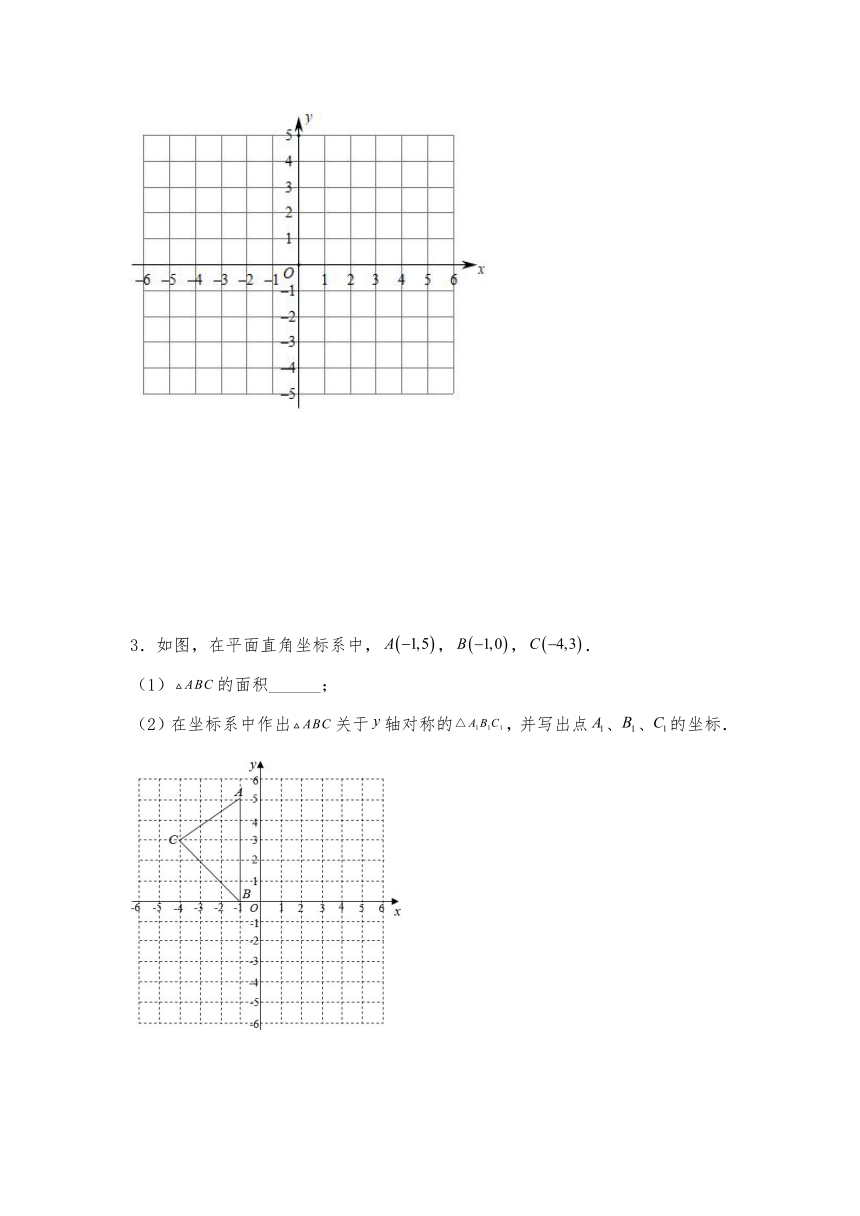
1.如图,已知A(﹣1,5),B(﹣1,1),C(﹣4,3).
(1)作出△ABC关于x轴对称的图形△A′B′C′;
(2)求△ABC的面积.
2.已知平面直角坐标系中,四边形ABCD四个顶点坐标分别为:A(﹣2,1),B(﹣3,﹣2),C(a+8,2a+8),D(1,2),且轴.
(1)点C的坐标为 ;
(2)在所给的平面直角坐标系中画出四边形ABCD.
(3)若网格中每个小正方形的边长均为1,则四边形ABCD的周长为 ;面积为 .
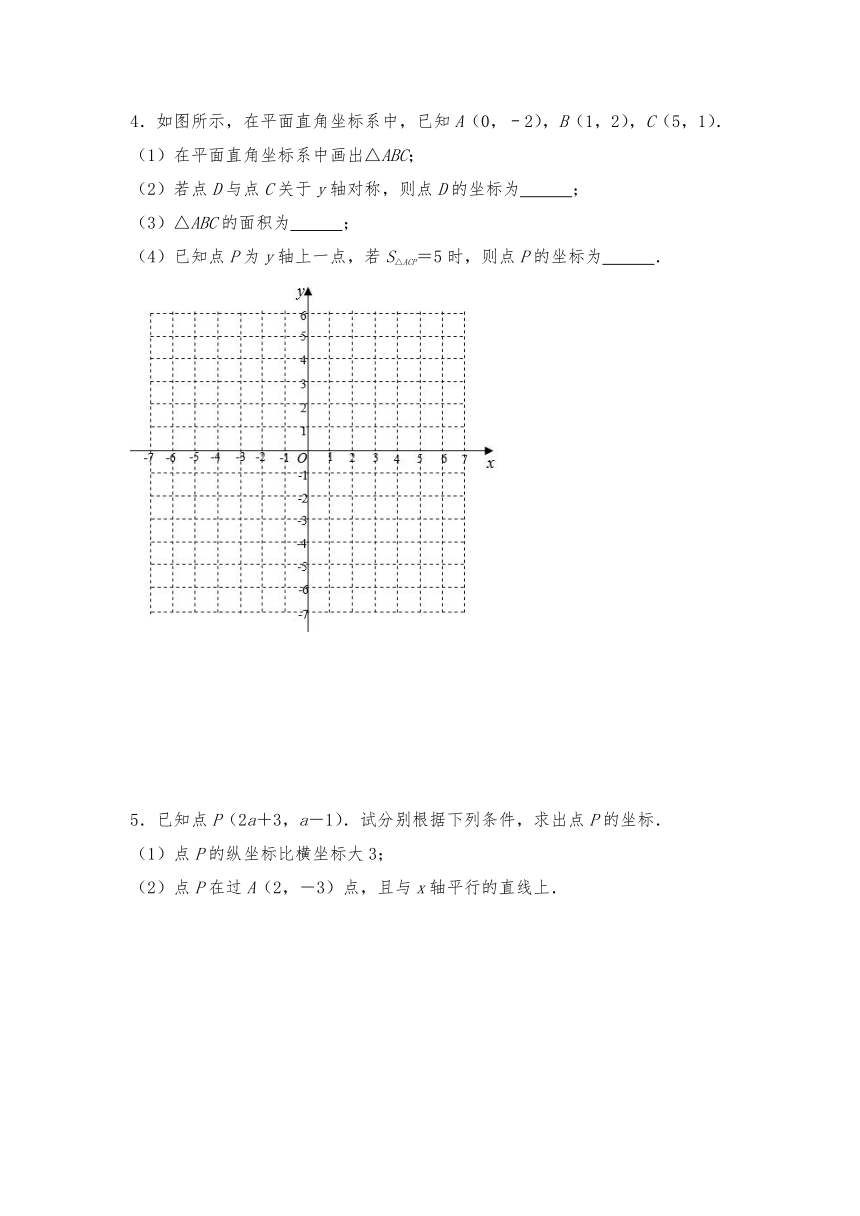
3.如图,在平面直角坐标系中,,,.
(1)的面积______;
(2)在坐标系中作出关于轴对称的,并写出点、、的坐标.
4.如图所示,在平面直角坐标系中,已知A(0,﹣2),B(1,2),C(5,1).
(1)在平面直角坐标系中画出△ABC;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)△ABC的面积为 ;
(4)已知点P为y轴上一点,若S△ACP=5时,则点P的坐标为 .
5.已知点P(2a+3,a-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,-3)点,且与x轴平行的直线上.
6.中,A、B、C三点坐标分别为、、.
(1)求的面积;
(2)若B、C点坐标不变,A点坐标变为,则的面积为______.
7.画出△ABC关于y轴对称的图形△A1B1C1.求:
(1)△A1B1C1三个顶点的坐标.
(2)△A1B1C1的面积.
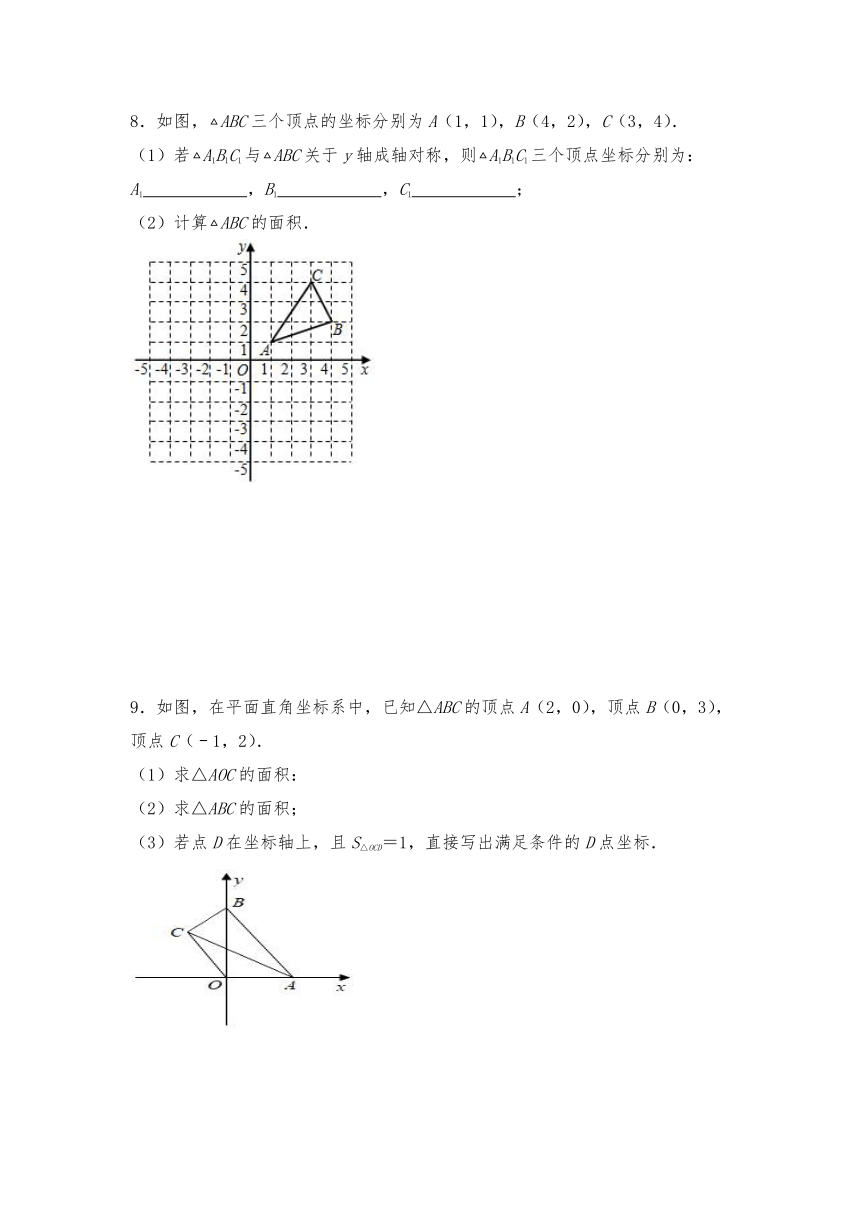
8.如图,ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)若A1B1C1与ABC关于y轴成轴对称,则A1B1C1三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)计算ABC的面积.
9.如图,在平面直角坐标系中,已知△ABC的顶点A(2,0),顶点B(0,3),顶点C(﹣1,2).
(1)求△AOC的面积:
(2)求△ABC的面积;
(3)若点D在坐标轴上,且S△OCD=1,直接写出满足条件的D点坐标.
10.已知A(0,0),B(9,O),C(7,5),D(2,7),求四边形ABCD的面积.
11.在如图的平面直角坐标系中:
(1)写出各点坐标:A ;C
(2)△ABC的面积为
(3)设点P在x轴上,且△ABP与△ABC的面积相等,点P的坐标为
12.如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)在网格中作出△ABC关于y轴对称的图形△A1B1C1;
(2)直接写出A1、B1、C1的坐标;
(3)若网格的单位长度为1,求△A1B1C1的面积.
13.如图,在平面直角坐标系中,O为坐标原点,点A(a,b)在第一象限,点B(﹣b﹣1,0),且实数a、b满足+(b﹣4)2=0
(1)求点A,B的坐标;
(2)若点P以2个单位长度/秒的速度从O点出发,沿x轴的负半轴运动,设点P运动时间为t秒,三角形ABP的面积为S,求S与t的关系式;
(3)在(2)的条件下,当t为何值时,S△ABP:S△AOP=2:3
14.如图,在平面直角坐标系中,△ABC的顶点均在网格的格点处.
(1)请写出A,B,C的坐标;
(2)请求出△ABC的面积;
(3)若点P在x轴上,且△PAB的面积与△ABC的面积相等,请直接写出点P的坐标.
15.如图,在平面直角坐标系中,已知是等边三角形,边上有一点,且、两点之间的距离为6.
(1)求的坐标(用含有的式子表示);
(2)如图,若点在线段上运动,点在轴的正半轴上运动.当的值最小时,.请求出此时的值.
(3)在(2)条件下,连接,请求出的值.
16.已知、、,当在y轴上,且的面积等于的面积时,求代数式的值.
17.如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足(a+8)2+=0,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是 ;
(2)如图(1)当P、Q分别在线段AO,OC上时,连接PB,QB,使S△PAB=2S△QBC,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请直接写出∠OPQ和∠PQB的数量关系.
18.已知:,,.
(1)在坐标系中描出各点,画出.
(2)求的面积;
(3)设点在轴上,且,求点的坐标.
19.如图,四边形OABC为长方形,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系.已知点A的坐标为(0,5),点C的坐标为(9,0).
(1)直接写出点B的坐标为 ;
(2)有一动点D从原点O出发,以1个单位长度/秒的速度沿线段OA向终点A运动,当直线CD将长方形的周长分为3:4两部分时,求D点的运动时间t值;
(3)在(2)的条件下,点E为坐标轴上一点,若三角形CDE的面积为18,直接写出点E的坐标.
20.如图1,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.
(1)求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图2,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
21.在平面直角坐标系中,画出点,点,点与点关于轴对称.
(1)连结、、,并画出的边上的中线.
(2)求出的面积.
答案
1.
解:(1)如图所示, 即为所求;
(2)如图所示:.
2.
解:(1)∵轴,
∴ ,
∴ ,
∴
∴
(2)如图:
(3)由图可知: , , ,
∴四边形ABCD的周长为 ,
如图:
四边形ABCD的面积等于:
.
3.
解:(1),
故答案为:7.5;
(2)如图,即为所求,并写出
4.
解:(1)在图中分别标记出三点,连接、、即可,如下图:
(2)点D与点C关于y轴对称,纵坐标不变,横坐标变为相反数
∵
∴
(3)由图形可知:△ABC的面积为长方形面积减去三个直角三角形的面积,
(4)设,则
,即,解得或
即或
5.
解:(1)∵点P(2a+3,a-1),且点P的纵坐标比横坐标大3,
∴a-1=2a+3+3,
解得a=-7,
∴点P(-11,-8);
(2)∵点P在过A(2,-3)点,且与x轴平行的直线上,
∴a-1=-3,
解得a=-2,
∴点P(-1,-3).
6.
解:(1)分别过点作的垂线交于两点,并反向延长,交于点,如下图:
则:、、、、、
由图形可得:
所以,
(2)分别过点作的垂线,分别相交于点,如下图:
则:、、、、
由图形可得:
所以,
7.
解:(1)如图所示:△A1B1C1三个顶点的坐标:A1(﹣3,4),B1(﹣1,2),C1(﹣5,1);
(2)3×4﹣×2×3﹣×2×2﹣×1×4=5.
8.
解:(1)∵A1B1C1与ABC关于y轴成轴对称,且A(1,1),B(4,2),C(3,4),
∴A1B1C1三个顶点坐标分别为:A1(﹣1,1),B1(﹣4,2),C1(﹣3,4);
故答案为:(﹣1,1);(﹣4,2);(﹣3,4);
(2)ABC的面积为3×3﹣﹣﹣
=9﹣1.5﹣1﹣3
=3.5.
9.
解:(1),
(2)过点C作CD垂直x轴,如下图:
,
.
(3)D点在y轴上时,,解得
yD=2或yD=﹣2,
此时D点(0,2),(0,﹣2),
D点在x轴上时,,解得
∴xD=1或xD=﹣1,
此时D点(﹣1,0),(1,0).
10.
解:过点C作CF⊥x轴于点F,过D作DE⊥x轴于点E
则AE=2,DE=7,BF=2,CF=5,EF=5
∴
.
11.解:(1)由图可得: , ;
(2)过点C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
则四边形DCEO为矩形,
∴
.
(3)设点P的坐标为(x,0),
则BP=|x 2|.
∵△ABP与△ABC的面积相等,
∴×1×|x 2|=4,
解得:x=10或x= 6,
∴点P的坐标为(10,0)或( 6,0),
12.
解:(1)按要求作出△ABC关于y轴对称的图形△A1B1C1如下:
(2)因为关于轴对称,横坐标不变纵坐标变为原来的相反数,即;
(3)如图:
,
,
.
13.
解:(1)∵a,b满足+(b﹣4)2=0,,(b﹣4)2≥0.
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴A(3,4),B(﹣5,0);
(2)过点A作AH⊥x轴于点H,AH=4,
分两种情况:
①点P在线段OB上(0≤t<),
如图1,BP=5﹣2t,
S===10﹣4t.
②点P在线段OB的延长线上(t>),
如图2,BP=2t﹣5,
S===4t﹣10.
(3)由题意可得,
分两种情况:
①点P在线段OB上(0≤t<),
∵S△ABP:S△AOP=2:3,
∴(10﹣4t):4t=2:3,
解得t=.
②点P在线段OB的延长线上(t>),
∵S△ABP:S△AOP=2:3,
∴(2t﹣5):2t=2:3,
解得t=.
综合以上可得,t=或时,S△ABP:S△AOP=2:3.
14.
解:解(1)由图可知,A(-3,-2),B(2,0),C(-1,2);
(2)S△ABC=S矩形ADEF-S△ADC-S△CEB-S△ABF,
=,
=,
=8;
(3)设,由点P在x轴上,点B也在x轴上,以PB为底,
∵点A到轴的距离为2,
∴△PAB的高为2,
∵S△PAB=S△ABC,
∴,
∴,
∵BP=|2-|,
∴|2-|=8,
解得或,
点P的坐标为(10,0)或(-6,0).
15.解:(1)∵边上有一点,且、两点之间的距离为6,
所以B点的横坐标为m-6,
∴点;
(2)如图,作点关于轴对称点,过点作,
由垂线段最短可得此时,的值最小,
∵,,,
∴,∴,
∴,∴,
(3)连接BP,
∵
∴
∴,
∴
,
∴.
16.解:∵在y轴上,
∴,
∴,
∵的面积等于的面积,
∴O、B到直线AC的距离相等,
∵A点的纵坐标为n+2=5,C点的纵坐标为n-1=2,
∴ AC与x轴不平行,
∴AC∥BO,
∴,
∴,
∴.
17.
解:(1)∵,
∴a+8=0,c+4=0,
∴a=﹣8,c=﹣4,
∴A(﹣8,0),B(﹣4,﹣4),C(0,﹣4),
∴BC//AO,
故答案为:平行;
(2)过B点作BE⊥AO于E,设时间经过t秒,S△PAB=4S△QBC,则AP=2t,OQ=t,BE=4,BC=4,CQ=4﹣t,
∴S△APB=AP BE=×2t×4=4t,S△BCQ=CQ BC=(4 t)×4=8 2t,
∵S△APB=4S△BCQ,
∴4t=4(8﹣2t)
解得,t= ,
∴AP=2t= ,
∴OP=OA﹣AP= ,
∴点P的坐标为(,0);
(3)∠PQB=∠OPQ+30°或∠BQP+∠OPQ=150°.理由如下:
当点Q在点C的上方时,过Q点作QH∥AO,如图2所示,
∴∠OPQ=∠PQH,
∵BC∥AO,QH∥AO,
∴QH∥BC,
∴∠HQB=∠CBQ=30°,
∴∠OPQ+∠CBQ=∠PQH+∠BQH,
∴∠PQB=∠OPQ+∠CBQ,即∠PQB=∠OPQ+30°;
②当点Q在点C的下方时;过Q点作HJ∥AO 如图3所示,
∴∠OPQ=∠PQJ,
∵BC∥AO,QH∥AO,
∴QH∥BC,
∴∠HQB=∠CBQ=30°,
∴∠HQB+∠BQP+∠PQJ=180°,
∴30°+∠BQP+∠OPQ=180°,
即∠BQP+∠OPQ=150°,
综上所述,∠PQB=∠OPQ+30°或∠BQP+∠OPQ=150°.
18.解:(1)如图所示:
(2)如(1)图,过点向、轴作垂线,垂足为、.
四边形的面积,
的面积,
的面积,
的面积.
的面积四边形的面积的面积的面积的面积;
(3)当点在轴上时,
,,
设点的坐标为,
解得:,.
点的坐标为或.
19.
解:(1)∵四边形OABC为长方形,
而点A的坐标为(0,5),点C的坐标为(9,0),
∴B点坐标为(9,5);
故答案为(9,5);
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,
∵直线CD将长方形OABC的周长分为3:4两部分,
∴(OD+OC):(AD+AB+BC)=3:4,
即(t+9):(5﹣t+9+5)=3:4,
∴t=3,
∴D点的运动时间为3 秒;
(3)由(2)得:D点坐标为(0,3),C点坐标为(9,0),
当E在x轴上时,设E点坐标为(a,0),
∵三角形CDE的面积是18,
∴×3×|9﹣a|=18,解得a=-3或a=21,
∴E点坐标为(-3,0)或(21,0).
当E在y轴上时,设E点坐标为(0,a),
∵三角形CDE的面积是18,
∴×9×|3﹣a|=18,解得a=﹣1或a=7,
∴E点坐标为(0,-1)或(0,7).
∴点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
20.
解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.
S△OBC=S梯形BCED+S△OBD-S△OCE
=(y1+y2)(x2-x1)+x1y1-x2y2
=(x2y1-x1y2).
∴△BOC的面积为(x2y1-x1y2).
(2)连接OB.
则有S四边形OABC=S△OAB+S△OBC
=(7×5-2×7)+(9×7-7×1)
=38.5.
∴四边形OABC的面积为38.5.
21.
解:∵点与点关于轴对称且,
∴
如下图所示,依次在图中画出点A、点B与点并连接即可,
又∵ 是边上的中线,
∴
如图所示,连接AE即可;
(2)
1.如图,已知A(﹣1,5),B(﹣1,1),C(﹣4,3).
(1)作出△ABC关于x轴对称的图形△A′B′C′;
(2)求△ABC的面积.
2.已知平面直角坐标系中,四边形ABCD四个顶点坐标分别为:A(﹣2,1),B(﹣3,﹣2),C(a+8,2a+8),D(1,2),且轴.
(1)点C的坐标为 ;
(2)在所给的平面直角坐标系中画出四边形ABCD.
(3)若网格中每个小正方形的边长均为1,则四边形ABCD的周长为 ;面积为 .
3.如图,在平面直角坐标系中,,,.
(1)的面积______;
(2)在坐标系中作出关于轴对称的,并写出点、、的坐标.
4.如图所示,在平面直角坐标系中,已知A(0,﹣2),B(1,2),C(5,1).
(1)在平面直角坐标系中画出△ABC;
(2)若点D与点C关于y轴对称,则点D的坐标为 ;
(3)△ABC的面积为 ;
(4)已知点P为y轴上一点,若S△ACP=5时,则点P的坐标为 .
5.已知点P(2a+3,a-1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,-3)点,且与x轴平行的直线上.
6.中,A、B、C三点坐标分别为、、.
(1)求的面积;
(2)若B、C点坐标不变,A点坐标变为,则的面积为______.
7.画出△ABC关于y轴对称的图形△A1B1C1.求:
(1)△A1B1C1三个顶点的坐标.
(2)△A1B1C1的面积.
8.如图,ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)若A1B1C1与ABC关于y轴成轴对称,则A1B1C1三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)计算ABC的面积.
9.如图,在平面直角坐标系中,已知△ABC的顶点A(2,0),顶点B(0,3),顶点C(﹣1,2).
(1)求△AOC的面积:
(2)求△ABC的面积;
(3)若点D在坐标轴上,且S△OCD=1,直接写出满足条件的D点坐标.
10.已知A(0,0),B(9,O),C(7,5),D(2,7),求四边形ABCD的面积.
11.在如图的平面直角坐标系中:
(1)写出各点坐标:A ;C
(2)△ABC的面积为
(3)设点P在x轴上,且△ABP与△ABC的面积相等,点P的坐标为
12.如图,在平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)在网格中作出△ABC关于y轴对称的图形△A1B1C1;
(2)直接写出A1、B1、C1的坐标;
(3)若网格的单位长度为1,求△A1B1C1的面积.
13.如图,在平面直角坐标系中,O为坐标原点,点A(a,b)在第一象限,点B(﹣b﹣1,0),且实数a、b满足+(b﹣4)2=0
(1)求点A,B的坐标;
(2)若点P以2个单位长度/秒的速度从O点出发,沿x轴的负半轴运动,设点P运动时间为t秒,三角形ABP的面积为S,求S与t的关系式;
(3)在(2)的条件下,当t为何值时,S△ABP:S△AOP=2:3
14.如图,在平面直角坐标系中,△ABC的顶点均在网格的格点处.
(1)请写出A,B,C的坐标;
(2)请求出△ABC的面积;
(3)若点P在x轴上,且△PAB的面积与△ABC的面积相等,请直接写出点P的坐标.
15.如图,在平面直角坐标系中,已知是等边三角形,边上有一点,且、两点之间的距离为6.
(1)求的坐标(用含有的式子表示);
(2)如图,若点在线段上运动,点在轴的正半轴上运动.当的值最小时,.请求出此时的值.
(3)在(2)条件下,连接,请求出的值.
16.已知、、,当在y轴上,且的面积等于的面积时,求代数式的值.
17.如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足(a+8)2+=0,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.
(1)直接写出点B的坐标,AO和BC位置关系是 ;
(2)如图(1)当P、Q分别在线段AO,OC上时,连接PB,QB,使S△PAB=2S△QBC,求出点P的坐标;
(3)在P、Q的运动过程中,当∠CBQ=30°时,请直接写出∠OPQ和∠PQB的数量关系.
18.已知:,,.
(1)在坐标系中描出各点,画出.
(2)求的面积;
(3)设点在轴上,且,求点的坐标.
19.如图,四边形OABC为长方形,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系.已知点A的坐标为(0,5),点C的坐标为(9,0).
(1)直接写出点B的坐标为 ;
(2)有一动点D从原点O出发,以1个单位长度/秒的速度沿线段OA向终点A运动,当直线CD将长方形的周长分为3:4两部分时,求D点的运动时间t值;
(3)在(2)的条件下,点E为坐标轴上一点,若三角形CDE的面积为18,直接写出点E的坐标.
20.如图1,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.
(1)求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图2,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
21.在平面直角坐标系中,画出点,点,点与点关于轴对称.
(1)连结、、,并画出的边上的中线.
(2)求出的面积.
答案
1.
解:(1)如图所示, 即为所求;
(2)如图所示:.
2.
解:(1)∵轴,
∴ ,
∴ ,
∴
∴
(2)如图:
(3)由图可知: , , ,
∴四边形ABCD的周长为 ,
如图:
四边形ABCD的面积等于:
.
3.
解:(1),
故答案为:7.5;
(2)如图,即为所求,并写出
4.
解:(1)在图中分别标记出三点,连接、、即可,如下图:
(2)点D与点C关于y轴对称,纵坐标不变,横坐标变为相反数
∵
∴
(3)由图形可知:△ABC的面积为长方形面积减去三个直角三角形的面积,
(4)设,则
,即,解得或
即或
5.
解:(1)∵点P(2a+3,a-1),且点P的纵坐标比横坐标大3,
∴a-1=2a+3+3,
解得a=-7,
∴点P(-11,-8);
(2)∵点P在过A(2,-3)点,且与x轴平行的直线上,
∴a-1=-3,
解得a=-2,
∴点P(-1,-3).
6.
解:(1)分别过点作的垂线交于两点,并反向延长,交于点,如下图:
则:、、、、、
由图形可得:
所以,
(2)分别过点作的垂线,分别相交于点,如下图:
则:、、、、
由图形可得:
所以,
7.
解:(1)如图所示:△A1B1C1三个顶点的坐标:A1(﹣3,4),B1(﹣1,2),C1(﹣5,1);
(2)3×4﹣×2×3﹣×2×2﹣×1×4=5.
8.
解:(1)∵A1B1C1与ABC关于y轴成轴对称,且A(1,1),B(4,2),C(3,4),
∴A1B1C1三个顶点坐标分别为:A1(﹣1,1),B1(﹣4,2),C1(﹣3,4);
故答案为:(﹣1,1);(﹣4,2);(﹣3,4);
(2)ABC的面积为3×3﹣﹣﹣
=9﹣1.5﹣1﹣3
=3.5.
9.
解:(1),
(2)过点C作CD垂直x轴,如下图:
,
.
(3)D点在y轴上时,,解得
yD=2或yD=﹣2,
此时D点(0,2),(0,﹣2),
D点在x轴上时,,解得
∴xD=1或xD=﹣1,
此时D点(﹣1,0),(1,0).
10.
解:过点C作CF⊥x轴于点F,过D作DE⊥x轴于点E
则AE=2,DE=7,BF=2,CF=5,EF=5
∴
.
11.解:(1)由图可得: , ;
(2)过点C作CD⊥x轴于D,CE⊥y轴于E,如图所示:
则四边形DCEO为矩形,
∴
.
(3)设点P的坐标为(x,0),
则BP=|x 2|.
∵△ABP与△ABC的面积相等,
∴×1×|x 2|=4,
解得:x=10或x= 6,
∴点P的坐标为(10,0)或( 6,0),
12.
解:(1)按要求作出△ABC关于y轴对称的图形△A1B1C1如下:
(2)因为关于轴对称,横坐标不变纵坐标变为原来的相反数,即;
(3)如图:
,
,
.
13.
解:(1)∵a,b满足+(b﹣4)2=0,,(b﹣4)2≥0.
∴a﹣3=0,b﹣4=0,
∴a=3,b=4,
∴A(3,4),B(﹣5,0);
(2)过点A作AH⊥x轴于点H,AH=4,
分两种情况:
①点P在线段OB上(0≤t<),
如图1,BP=5﹣2t,
S===10﹣4t.
②点P在线段OB的延长线上(t>),
如图2,BP=2t﹣5,
S===4t﹣10.
(3)由题意可得,
分两种情况:
①点P在线段OB上(0≤t<),
∵S△ABP:S△AOP=2:3,
∴(10﹣4t):4t=2:3,
解得t=.
②点P在线段OB的延长线上(t>),
∵S△ABP:S△AOP=2:3,
∴(2t﹣5):2t=2:3,
解得t=.
综合以上可得,t=或时,S△ABP:S△AOP=2:3.
14.
解:解(1)由图可知,A(-3,-2),B(2,0),C(-1,2);
(2)S△ABC=S矩形ADEF-S△ADC-S△CEB-S△ABF,
=,
=,
=8;
(3)设,由点P在x轴上,点B也在x轴上,以PB为底,
∵点A到轴的距离为2,
∴△PAB的高为2,
∵S△PAB=S△ABC,
∴,
∴,
∵BP=|2-|,
∴|2-|=8,
解得或,
点P的坐标为(10,0)或(-6,0).
15.解:(1)∵边上有一点,且、两点之间的距离为6,
所以B点的横坐标为m-6,
∴点;
(2)如图,作点关于轴对称点,过点作,
由垂线段最短可得此时,的值最小,
∵,,,
∴,∴,
∴,∴,
(3)连接BP,
∵
∴
∴,
∴
,
∴.
16.解:∵在y轴上,
∴,
∴,
∵的面积等于的面积,
∴O、B到直线AC的距离相等,
∵A点的纵坐标为n+2=5,C点的纵坐标为n-1=2,
∴ AC与x轴不平行,
∴AC∥BO,
∴,
∴,
∴.
17.
解:(1)∵,
∴a+8=0,c+4=0,
∴a=﹣8,c=﹣4,
∴A(﹣8,0),B(﹣4,﹣4),C(0,﹣4),
∴BC//AO,
故答案为:平行;
(2)过B点作BE⊥AO于E,设时间经过t秒,S△PAB=4S△QBC,则AP=2t,OQ=t,BE=4,BC=4,CQ=4﹣t,
∴S△APB=AP BE=×2t×4=4t,S△BCQ=CQ BC=(4 t)×4=8 2t,
∵S△APB=4S△BCQ,
∴4t=4(8﹣2t)
解得,t= ,
∴AP=2t= ,
∴OP=OA﹣AP= ,
∴点P的坐标为(,0);
(3)∠PQB=∠OPQ+30°或∠BQP+∠OPQ=150°.理由如下:
当点Q在点C的上方时,过Q点作QH∥AO,如图2所示,
∴∠OPQ=∠PQH,
∵BC∥AO,QH∥AO,
∴QH∥BC,
∴∠HQB=∠CBQ=30°,
∴∠OPQ+∠CBQ=∠PQH+∠BQH,
∴∠PQB=∠OPQ+∠CBQ,即∠PQB=∠OPQ+30°;
②当点Q在点C的下方时;过Q点作HJ∥AO 如图3所示,
∴∠OPQ=∠PQJ,
∵BC∥AO,QH∥AO,
∴QH∥BC,
∴∠HQB=∠CBQ=30°,
∴∠HQB+∠BQP+∠PQJ=180°,
∴30°+∠BQP+∠OPQ=180°,
即∠BQP+∠OPQ=150°,
综上所述,∠PQB=∠OPQ+30°或∠BQP+∠OPQ=150°.
18.解:(1)如图所示:
(2)如(1)图,过点向、轴作垂线,垂足为、.
四边形的面积,
的面积,
的面积,
的面积.
的面积四边形的面积的面积的面积的面积;
(3)当点在轴上时,
,,
设点的坐标为,
解得:,.
点的坐标为或.
19.
解:(1)∵四边形OABC为长方形,
而点A的坐标为(0,5),点C的坐标为(9,0),
∴B点坐标为(9,5);
故答案为(9,5);
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,
∵直线CD将长方形OABC的周长分为3:4两部分,
∴(OD+OC):(AD+AB+BC)=3:4,
即(t+9):(5﹣t+9+5)=3:4,
∴t=3,
∴D点的运动时间为3 秒;
(3)由(2)得:D点坐标为(0,3),C点坐标为(9,0),
当E在x轴上时,设E点坐标为(a,0),
∵三角形CDE的面积是18,
∴×3×|9﹣a|=18,解得a=-3或a=21,
∴E点坐标为(-3,0)或(21,0).
当E在y轴上时,设E点坐标为(0,a),
∵三角形CDE的面积是18,
∴×9×|3﹣a|=18,解得a=﹣1或a=7,
∴E点坐标为(0,-1)或(0,7).
∴点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
20.
解:(1)过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.
S△OBC=S梯形BCED+S△OBD-S△OCE
=(y1+y2)(x2-x1)+x1y1-x2y2
=(x2y1-x1y2).
∴△BOC的面积为(x2y1-x1y2).
(2)连接OB.
则有S四边形OABC=S△OAB+S△OBC
=(7×5-2×7)+(9×7-7×1)
=38.5.
∴四边形OABC的面积为38.5.
21.
解:∵点与点关于轴对称且,
∴
如下图所示,依次在图中画出点A、点B与点并连接即可,
又∵ 是边上的中线,
∴
如图所示,连接AE即可;
(2)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
