八年级数学上册试题 6.2中位数与众数-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 6.2中位数与众数-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 143.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 23:22:19 | ||
图片预览



文档简介
6.2中位数与众数
一、选择题
1.数据 -1,0,1,2,-2的中位数是( )
A.-1 B.0 C.1 D.2
2.在抗击新型冠状病毒肺炎疫情中,某社区志愿者小分队10名队员年龄统计如下表:则这10名队员年龄的中位数、众数分别是( )
年龄(岁)
人数
A.20岁,35岁 B.26岁,22岁 C.22岁,26岁 D.30岁,30岁
3.下列说法中,正确的是( )
A.一组数据的众数一定只有一个.
B.一组数据的众数是6,则这组数据中出现次数最多的数据是6.
C.一组数据的中位数一定是这组数据中的某一个数据.
D.一组数据中的最大的数据增大时,这组数据的中位数也随之增大.
4.一家鞋店在一段时间内销售某种女鞋30双,各种尺码鞋的销售量如下表所示,在鞋的尺码组成的数据中,这组数据的众数是( )
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
A.23.5 B.11 C.24 D.7
5.某班班主任调查了本班学生一周的居家体育锻炼时间,统计数据如下表所示:
时间(小时) 7 8 9 10 11
人数(人) 8 5 7 12 8
则该班学生一周的居家体育锻炼时间的中位数和众数分别是( )
A.9,10 B.9.5,10 C.10,10 D.9.5,11
6.小红在班上做节水意识调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:5,5,6,7,8,9,10.她发现,若去掉其中两个数据后,这组数据的中位数、众数保持不变,则去掉的两个数可能是( )
A.5,10 B.5,9 C.6,8 D.7,8
7.新冠肺炎疫情期间,某市实施静态管理,九年级某班组建了若干个数学学习互助小组,其中一个9人小组进行数学线上学习效果的自测,九名学生的平均成绩为73分,若将他们的成绩从高分到低分排序后,前五名学生的平均成绩为85分,后五名学生的平均成绩为63分,则这九名学生成绩的中位数是( )
A.84 B.83 C.74 D.73
8.某装配车间为了较合理地确定每名工人标准目产量,车间管理者从过去的工作日中随机地抽查了该车间15名工人在某一天中各自装配机器的数量(单位:台),具体如下:6,7,7,8,8,8,8,9,10,10,11,13,15,15,16.根据抽样的数据,车间管理者将每名工人标准日产量定为9台,其依据是统计数据中的( )
A.最大数据 B.众数 C.中位数 D.平均数
9.以下是某校八年级10名同学参加创建“文明校园”演讲比赛的统计表:
成绩(分) 80 85 90 95
人数(人) 1 2 5 2
则这组数据的众数是( )
A.85 B.90 C.90.5 D.95
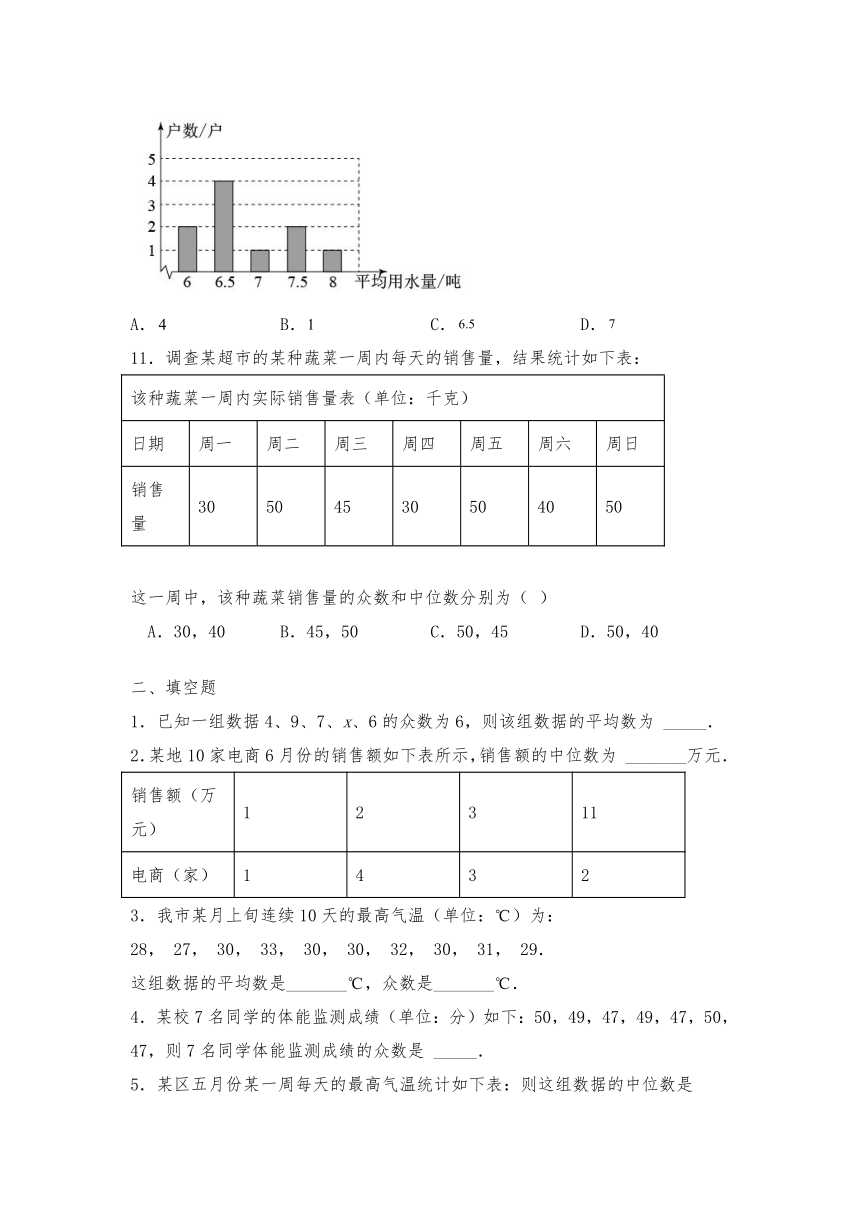
10.为了解班级同学的家庭用水状况,小明在全班50名同学中随机调查了10名同学家庭中一年的月平均用水量(单位:吨),绘制了条形统计图如图,这10名同学家庭中一年的月平均用水量的中位数是( )
B. C. D.
11.调查某超市的某种蔬菜一周内每天的销售量,结果统计如下表:
该种蔬菜一周内实际销售量表(单位:千克)
日期 周一 周二 周三 周四 周五 周六 周日
销售量 30 50 45 30 50 40 50
这一周中,该种蔬菜销售量的众数和中位数分别为( )
A.30,40 B.45,50 C.50,45 D.50,40
二、填空题
1.已知一组数据4、9、7、x、6的众数为6,则该组数据的平均数为 _____.
2.某地10家电商6月份的销售额如下表所示,销售额的中位数为 _______万元.
销售额(万元) 1 2 3 11
电商(家) 1 4 3 2
3.我市某月上旬连续10天的最高气温(单位:℃)为:
28, 27, 30, 33, 30, 30, 32, 30, 31, 29.
这组数据的平均数是_______℃,众数是_______℃.
4.某校7名同学的体能监测成绩(单位:分)如下:50,49,47,49,47,50,47,则7名同学体能监测成绩的众数是 _____.
5.某区五月份某一周每天的最高气温统计如下表:则这组数据的中位数是______℃,众数是______ ℃.
最高气温(℃) 22 24 25 27
天数 2 3 1 1
6.在一次有10人参加的数学测试中,得100分,95分,85分,75分的人数分别是1,3,4,2,那么这组数据的中位数是______分.
7.东门某商场试销一种新款衬衫,一周内销售情况如下表所示:
型号(厘米) 38 39 40 41 42 43
数量(件) 25 30 36 50 28 8
商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是________.(填“平均数”或“中位数”或“众数”)
8.“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别是:6,8,9,15,15.这组数据的中位数、众数分别为______、___________.
三、解答题
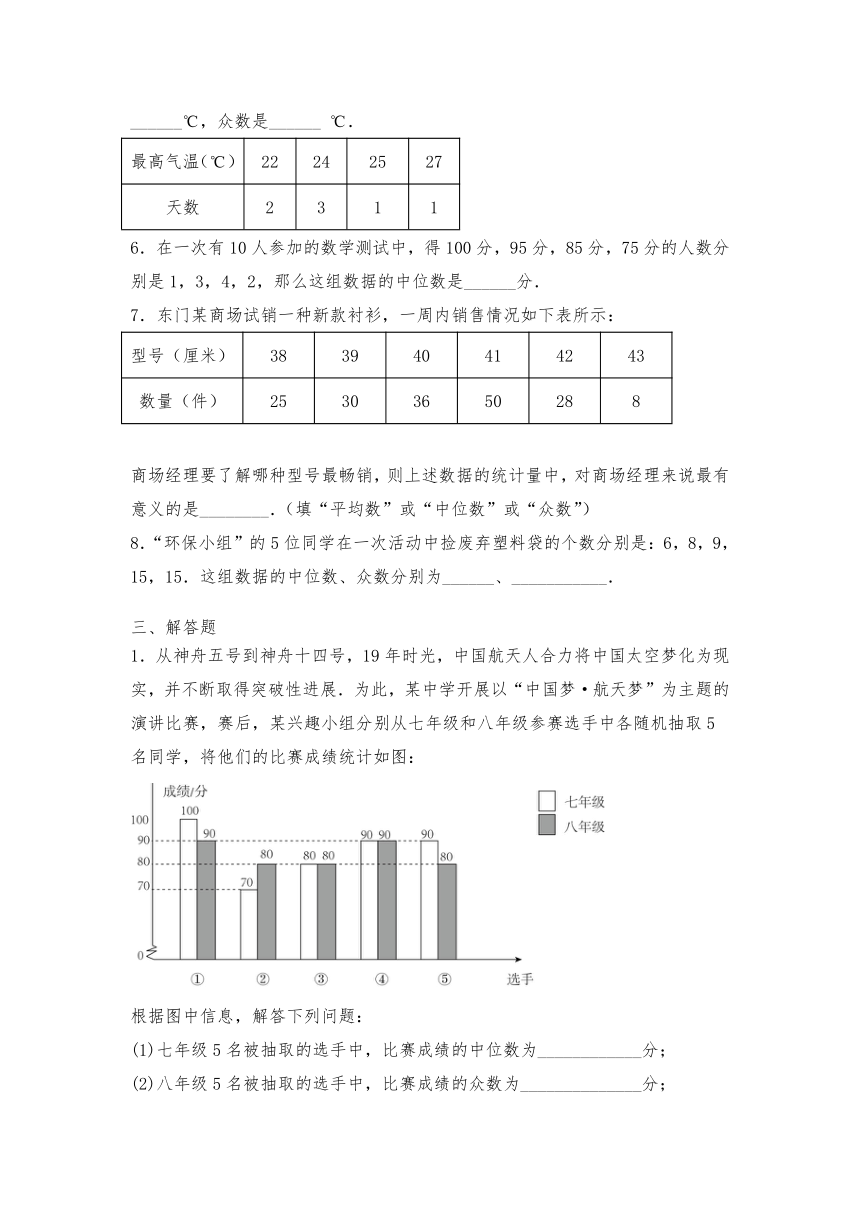
1.从神舟五号到神舟十四号,19年时光,中国航天人合力将中国太空梦化为现实,并不断取得突破性进展.为此,某中学开展以“中国梦·航天梦”为主题的演讲比赛,赛后,某兴趣小组分别从七年级和八年级参赛选手中各随机抽取5名同学,将他们的比赛成绩统计如图:
根据图中信息,解答下列问题:
(1)七年级5名被抽取的选手中,比赛成绩的中位数为____________分;
(2)八年级5名被抽取的选手中,比赛成绩的众数为______________分;
(3)分别计算两个年级被抽取的选手的平均成绩,并估计哪个年级的平均成绩较高?
2.某公司有15名员工,他们所在部门及相应每人所创年利润如表所示.
部门 人数 每人所创年利润/万元
A 5 3
B 2 8
C 1 7
D 4 4
E 3 9
(1)指出这个公司年利润的众数、中位数;
(2)这个公司平均每人所创年利润是多少?
(3)公司规定,个人所创年利润由高到低前40%的人可以获奖.试判断D部门的员工能否获奖,并说明理由.
3.某校开展了“学党史,知党恩,跟党走”的知识竞赛.现从该校七、八年级中各随机抽取20名学生的竞赛成绩进行调查:
【收集数据】
七年级:70,74,74,76,78,78,80,80,82,85,88,88,94,95,98,100,100,100,100,100;
八年级:64,68,70,72,74,80,82,82,84,86,90,92,98,98,100,100,100,100,100,100
【分析数据】两组数据的平均数、众数、中位数如表:
年级 平均数 众数 中位数
七年级 87 100 a
八年级 87 b 88
根据以上信息,解答下列问题:
(1)直接写出上述表格中a,b的值;
(2)根据以上样本数据,你认为该校七、八年级中哪个年级学生对“党史”掌握较好?请说明理由;
(3)若成绩在80分以上(含80分)为优秀,该校七、八年级共有800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
4.2020年东京奥运会于2021年7月23日至8月8日举行,跳水比赛是大家最喜爱观看的项目之一,其计分规则如下:
a.每次试跳的动作,按照其完成难度的不同对应一个难度系数H;
b.每次试跳都有7名裁判进行打分(0~10分,分数为0.5的整数倍),在7个得分中去掉2个最高分和2个最低分,剩下3个得分的平均值为这次试跳的完成分p;
c.运动员该次试跳的得分A=难度系数H×完成分p×3
在比赛中,某运动员一次试跳后的打分表为:
难度系数 裁判 1# 2# 3# 4# 5# 6# 7#
3.5 打分 7.5 8.5 7.5 9.0 7.5 8.5 8.0
(1)7名裁判打分的众数是 ;中位数是 .
(2)该运动员本次试跳的得分是多少?
5.某校对八年级甲、乙两班各60名学生进行知识测试,测试完成后分别抽取了12份成绩,整理分析过程如下.
【收集数据】
甲班12名学生测试成绩(单位:分)统计如下:45,59,60,38,57,53,52,58,60,50,43,49;
乙班12名学生测试成绩(单位:分)统计如下:35,55,46,39,54,47,43,57.42,59,60.47.
【整理数据】
按如下分数段整理,描述这两组样本数据:
组别频数 班级 35≦x<40 40≦x<45 45≦x<50 50≦x<55 55≦x<60
甲班 1 1 2 3 5
乙班 2 2 3 1 4
【分析数据】
两组样本数据的平均数、众数、中位数如表所示,根据以上信息回答下列问题:
班级 平均数 众数 中位数
甲班 52 a 52.5
乙班 48.7 47 b
(1)__________,__________;
(2)若规定成绩在40分及以上为合格,请估计乙班60名学生中知识测试成绩合格的学生有多少人;
(3)你认为哪个班的学生知识测试成绩的整体水平较好,请说出一条理由.
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.B.A.B.C.B.C.B.C.C.
二、填空题
1.6.4.
2..
3.30,30
4..
5.24,24.
6.85.
7.众数.
8.9,15.
三、解答题
1.(1)
解:由图可把七年级5名选手的成绩按从小到大顺序排列为70、80、90、90、100,所以他们比赛成绩的中位数为90分;
故答案为90;
(2)
解:由统计图可知:八年级5名选手中,成绩为80分的出现了三次,所以他们比赛成绩的众数为80分;
故答案为80;
(3)
解:七年级5名选手的平均成绩为(分);
八年级5名选手的平均成绩为(分);
∵86>84,
∴估计七年级的平均成绩较高.
2.(1)
解:由题意可得,
这15名员工的每人创年利润为:9、9、9、8、8、7、4、4、4、4、3、3、3、3、3,
∴这组数据的众数是3,中位数是4.
(2)
公司平均每人所创年利润(万元).
∴这个公司平均每人所创年利润是多少万元.
(3)
D部门员工不能获奖.
理由:获奖人数为:(人)
个人所创年利润由高到低分别为E部门3人,B部门2人,C部门1人,共6人,而本组数据的中位数是4,按个人所创年利润由高到低排在本组数据的第7位.
∴D部门的员工不能获奖.
3.(1)
解:,b=100;
(2)
八年级学生对“党史”掌握的比较好,
因为七年级和八年级学生的平均分和众数相同,但八年级学生的中位数大于七年级;
(3)
七年级抽取的学生成绩在80分及以上的人数为14人,
八年级抽取的学生成绩在80分及以上的人数为15人,
估计该校七,八年级参加此次竞赛活动成绩优秀的学生人数为800=580(人).
4.解:(1)7.5出现的次数最多,7名裁判打分的众数是7.5;
将这组数据按照从小到大的顺序排列得:7.5、7.5、7.5、8.0、8.5、8.5、9.0,根据中位数的定义可得,中位数为8.0;
故答案为:7.5,8.0;
(2)根据试跳得分公式可得:
(分),
故该运动员本次试跳得分为84分.
5.(1)
解:∵甲班12名学生测试成绩中得60分的有两个,人数最多,
∴甲班的众数a=60,
将乙班成绩按从小到大的顺序排列为:35,39,42,43,46,47,47,54,55,57,59,60,
∴处在最中间位置的两个数是47和47,
∴乙班的中位数b=,
故答案为:60,47;
(2)
(人),
答:估计乙班60名学生中知识测试成绩合格的学生约有50人;
(3)
甲班的学生知识测试成绩的整体水平较好,
理由:∵样本中甲班成绩的平均数和众数均高于乙班,
∴甲班的学生知识测试成绩的整体水平较好.
一、选择题
1.数据 -1,0,1,2,-2的中位数是( )
A.-1 B.0 C.1 D.2
2.在抗击新型冠状病毒肺炎疫情中,某社区志愿者小分队10名队员年龄统计如下表:则这10名队员年龄的中位数、众数分别是( )
年龄(岁)
人数
A.20岁,35岁 B.26岁,22岁 C.22岁,26岁 D.30岁,30岁
3.下列说法中,正确的是( )
A.一组数据的众数一定只有一个.
B.一组数据的众数是6,则这组数据中出现次数最多的数据是6.
C.一组数据的中位数一定是这组数据中的某一个数据.
D.一组数据中的最大的数据增大时,这组数据的中位数也随之增大.
4.一家鞋店在一段时间内销售某种女鞋30双,各种尺码鞋的销售量如下表所示,在鞋的尺码组成的数据中,这组数据的众数是( )
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
A.23.5 B.11 C.24 D.7
5.某班班主任调查了本班学生一周的居家体育锻炼时间,统计数据如下表所示:
时间(小时) 7 8 9 10 11
人数(人) 8 5 7 12 8
则该班学生一周的居家体育锻炼时间的中位数和众数分别是( )
A.9,10 B.9.5,10 C.10,10 D.9.5,11
6.小红在班上做节水意识调查,收集了班上7位同学家里上个月的用水量(单位:吨)如下:5,5,6,7,8,9,10.她发现,若去掉其中两个数据后,这组数据的中位数、众数保持不变,则去掉的两个数可能是( )
A.5,10 B.5,9 C.6,8 D.7,8
7.新冠肺炎疫情期间,某市实施静态管理,九年级某班组建了若干个数学学习互助小组,其中一个9人小组进行数学线上学习效果的自测,九名学生的平均成绩为73分,若将他们的成绩从高分到低分排序后,前五名学生的平均成绩为85分,后五名学生的平均成绩为63分,则这九名学生成绩的中位数是( )
A.84 B.83 C.74 D.73
8.某装配车间为了较合理地确定每名工人标准目产量,车间管理者从过去的工作日中随机地抽查了该车间15名工人在某一天中各自装配机器的数量(单位:台),具体如下:6,7,7,8,8,8,8,9,10,10,11,13,15,15,16.根据抽样的数据,车间管理者将每名工人标准日产量定为9台,其依据是统计数据中的( )
A.最大数据 B.众数 C.中位数 D.平均数
9.以下是某校八年级10名同学参加创建“文明校园”演讲比赛的统计表:
成绩(分) 80 85 90 95
人数(人) 1 2 5 2
则这组数据的众数是( )
A.85 B.90 C.90.5 D.95
10.为了解班级同学的家庭用水状况,小明在全班50名同学中随机调查了10名同学家庭中一年的月平均用水量(单位:吨),绘制了条形统计图如图,这10名同学家庭中一年的月平均用水量的中位数是( )
B. C. D.
11.调查某超市的某种蔬菜一周内每天的销售量,结果统计如下表:
该种蔬菜一周内实际销售量表(单位:千克)
日期 周一 周二 周三 周四 周五 周六 周日
销售量 30 50 45 30 50 40 50
这一周中,该种蔬菜销售量的众数和中位数分别为( )
A.30,40 B.45,50 C.50,45 D.50,40
二、填空题
1.已知一组数据4、9、7、x、6的众数为6,则该组数据的平均数为 _____.
2.某地10家电商6月份的销售额如下表所示,销售额的中位数为 _______万元.
销售额(万元) 1 2 3 11
电商(家) 1 4 3 2
3.我市某月上旬连续10天的最高气温(单位:℃)为:
28, 27, 30, 33, 30, 30, 32, 30, 31, 29.
这组数据的平均数是_______℃,众数是_______℃.
4.某校7名同学的体能监测成绩(单位:分)如下:50,49,47,49,47,50,47,则7名同学体能监测成绩的众数是 _____.
5.某区五月份某一周每天的最高气温统计如下表:则这组数据的中位数是______℃,众数是______ ℃.
最高气温(℃) 22 24 25 27
天数 2 3 1 1
6.在一次有10人参加的数学测试中,得100分,95分,85分,75分的人数分别是1,3,4,2,那么这组数据的中位数是______分.
7.东门某商场试销一种新款衬衫,一周内销售情况如下表所示:
型号(厘米) 38 39 40 41 42 43
数量(件) 25 30 36 50 28 8
商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是________.(填“平均数”或“中位数”或“众数”)
8.“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别是:6,8,9,15,15.这组数据的中位数、众数分别为______、___________.
三、解答题
1.从神舟五号到神舟十四号,19年时光,中国航天人合力将中国太空梦化为现实,并不断取得突破性进展.为此,某中学开展以“中国梦·航天梦”为主题的演讲比赛,赛后,某兴趣小组分别从七年级和八年级参赛选手中各随机抽取5名同学,将他们的比赛成绩统计如图:
根据图中信息,解答下列问题:
(1)七年级5名被抽取的选手中,比赛成绩的中位数为____________分;
(2)八年级5名被抽取的选手中,比赛成绩的众数为______________分;
(3)分别计算两个年级被抽取的选手的平均成绩,并估计哪个年级的平均成绩较高?
2.某公司有15名员工,他们所在部门及相应每人所创年利润如表所示.
部门 人数 每人所创年利润/万元
A 5 3
B 2 8
C 1 7
D 4 4
E 3 9
(1)指出这个公司年利润的众数、中位数;
(2)这个公司平均每人所创年利润是多少?
(3)公司规定,个人所创年利润由高到低前40%的人可以获奖.试判断D部门的员工能否获奖,并说明理由.
3.某校开展了“学党史,知党恩,跟党走”的知识竞赛.现从该校七、八年级中各随机抽取20名学生的竞赛成绩进行调查:
【收集数据】
七年级:70,74,74,76,78,78,80,80,82,85,88,88,94,95,98,100,100,100,100,100;
八年级:64,68,70,72,74,80,82,82,84,86,90,92,98,98,100,100,100,100,100,100
【分析数据】两组数据的平均数、众数、中位数如表:
年级 平均数 众数 中位数
七年级 87 100 a
八年级 87 b 88
根据以上信息,解答下列问题:
(1)直接写出上述表格中a,b的值;
(2)根据以上样本数据,你认为该校七、八年级中哪个年级学生对“党史”掌握较好?请说明理由;
(3)若成绩在80分以上(含80分)为优秀,该校七、八年级共有800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
4.2020年东京奥运会于2021年7月23日至8月8日举行,跳水比赛是大家最喜爱观看的项目之一,其计分规则如下:
a.每次试跳的动作,按照其完成难度的不同对应一个难度系数H;
b.每次试跳都有7名裁判进行打分(0~10分,分数为0.5的整数倍),在7个得分中去掉2个最高分和2个最低分,剩下3个得分的平均值为这次试跳的完成分p;
c.运动员该次试跳的得分A=难度系数H×完成分p×3
在比赛中,某运动员一次试跳后的打分表为:
难度系数 裁判 1# 2# 3# 4# 5# 6# 7#
3.5 打分 7.5 8.5 7.5 9.0 7.5 8.5 8.0
(1)7名裁判打分的众数是 ;中位数是 .
(2)该运动员本次试跳的得分是多少?
5.某校对八年级甲、乙两班各60名学生进行知识测试,测试完成后分别抽取了12份成绩,整理分析过程如下.
【收集数据】
甲班12名学生测试成绩(单位:分)统计如下:45,59,60,38,57,53,52,58,60,50,43,49;
乙班12名学生测试成绩(单位:分)统计如下:35,55,46,39,54,47,43,57.42,59,60.47.
【整理数据】
按如下分数段整理,描述这两组样本数据:
组别频数 班级 35≦x<40 40≦x<45 45≦x<50 50≦x<55 55≦x<60
甲班 1 1 2 3 5
乙班 2 2 3 1 4
【分析数据】
两组样本数据的平均数、众数、中位数如表所示,根据以上信息回答下列问题:
班级 平均数 众数 中位数
甲班 52 a 52.5
乙班 48.7 47 b
(1)__________,__________;
(2)若规定成绩在40分及以上为合格,请估计乙班60名学生中知识测试成绩合格的学生有多少人;
(3)你认为哪个班的学生知识测试成绩的整体水平较好,请说出一条理由.
【中小学教辅资源店 微信:mlxt2022】
答案
一、选择题
B.B.B.A.B.C.B.C.B.C.C.
二、填空题
1.6.4.
2..
3.30,30
4..
5.24,24.
6.85.
7.众数.
8.9,15.
三、解答题
1.(1)
解:由图可把七年级5名选手的成绩按从小到大顺序排列为70、80、90、90、100,所以他们比赛成绩的中位数为90分;
故答案为90;
(2)
解:由统计图可知:八年级5名选手中,成绩为80分的出现了三次,所以他们比赛成绩的众数为80分;
故答案为80;
(3)
解:七年级5名选手的平均成绩为(分);
八年级5名选手的平均成绩为(分);
∵86>84,
∴估计七年级的平均成绩较高.
2.(1)
解:由题意可得,
这15名员工的每人创年利润为:9、9、9、8、8、7、4、4、4、4、3、3、3、3、3,
∴这组数据的众数是3,中位数是4.
(2)
公司平均每人所创年利润(万元).
∴这个公司平均每人所创年利润是多少万元.
(3)
D部门员工不能获奖.
理由:获奖人数为:(人)
个人所创年利润由高到低分别为E部门3人,B部门2人,C部门1人,共6人,而本组数据的中位数是4,按个人所创年利润由高到低排在本组数据的第7位.
∴D部门的员工不能获奖.
3.(1)
解:,b=100;
(2)
八年级学生对“党史”掌握的比较好,
因为七年级和八年级学生的平均分和众数相同,但八年级学生的中位数大于七年级;
(3)
七年级抽取的学生成绩在80分及以上的人数为14人,
八年级抽取的学生成绩在80分及以上的人数为15人,
估计该校七,八年级参加此次竞赛活动成绩优秀的学生人数为800=580(人).
4.解:(1)7.5出现的次数最多,7名裁判打分的众数是7.5;
将这组数据按照从小到大的顺序排列得:7.5、7.5、7.5、8.0、8.5、8.5、9.0,根据中位数的定义可得,中位数为8.0;
故答案为:7.5,8.0;
(2)根据试跳得分公式可得:
(分),
故该运动员本次试跳得分为84分.
5.(1)
解:∵甲班12名学生测试成绩中得60分的有两个,人数最多,
∴甲班的众数a=60,
将乙班成绩按从小到大的顺序排列为:35,39,42,43,46,47,47,54,55,57,59,60,
∴处在最中间位置的两个数是47和47,
∴乙班的中位数b=,
故答案为:60,47;
(2)
(人),
答:估计乙班60名学生中知识测试成绩合格的学生约有50人;
(3)
甲班的学生知识测试成绩的整体水平较好,
理由:∵样本中甲班成绩的平均数和众数均高于乙班,
∴甲班的学生知识测试成绩的整体水平较好.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
