北师大版数学七年级上册4.5多边形和圆的初步认识 同步练习(含答案)
文档属性
| 名称 | 北师大版数学七年级上册4.5多边形和圆的初步认识 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 09:38:39 | ||
图片预览


文档简介
4.5多边形和圆的初步认识
一、选择题
1. 下列各组图形都是平面图形的一组是( )
A. 线段、圆、圆锥、球 B. 角、三角形、长方形、圆柱
C. 长方体、圆柱、棱锥、球 D. 圆、三角形、正方形、长方形
2. 从六边形的一个顶点出发,可引出的对角线共有( )
A. 1条 B. 2条 C. 3条 D. 4条
3. 下列正多边形中,能够铺满地面的是( )
A. 正方形 B. 正五边形 C. 正七边形 D. 正九边形
4.关于正多边形的概念,下列说法正确的是( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等或各角相等的多边形是正多边形
D.各边相等且各角相等的多边形是正多边形
5.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
6.下列说法正确的个数为( )
①连接C,D两点的线段叫两点之间的距离
②两点之间直线最短
③射线上点的个数是直线上点的个数的一半
④n边形从其中一个顶点出发连接其余各顶点,可以画出(n-3)条对角线,这些对角线把这个n边形分成了(n-2)个三角形
A.3个 B.2个 C.1个 D.0个
7.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为( )
A.2001 B.2005 C.2004 D.2006
二、填空题
1. 一个圆的直径是4cm,周长是______cm.
2. 用正六边形的瓷砖铺满地面,围绕一点拼在一起的正六边形瓷砖的块数是______块.
3.一个多边形从一个顶点引出的对角线有6条,则此多边形的边数是________ 条.
4.我们把各边相等,且各角也相等的多边形叫做正多边形,如图,边长相等的正五边形和正方形的一边重合,则________°.
5.将一个圆分成四个扇形,它们的圆心角的度数比为2:4:5:7,则最大扇形的圆心角是__.
6.从n边形的一个顶点出发,分别连接这个点与同它不相邻的各个顶点,得到7个三角形,那么这个多边形为______边形.
7.若一个多边形从一个顶点出发可以引7条对角线,则这个多边形共有______条对角线.
8.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
9.已知从六边形的一个顶点出发,可以引条对角线,这些对角线可以把这个六边形分成个三角形,则______.
三、解答题
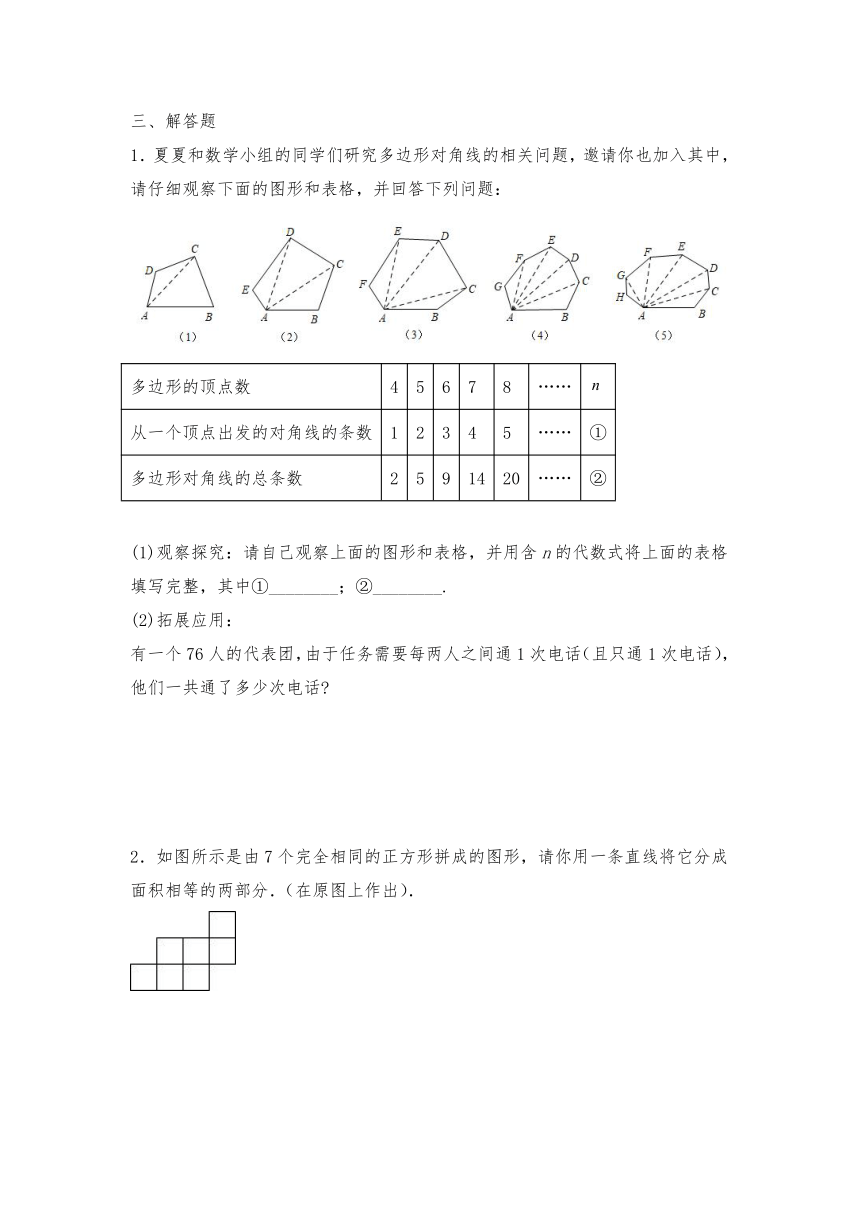
1.夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
2.如图所示是由7个完全相同的正方形拼成的图形,请你用一条直线将它分成面积相等的两部分.(在原图上作出).
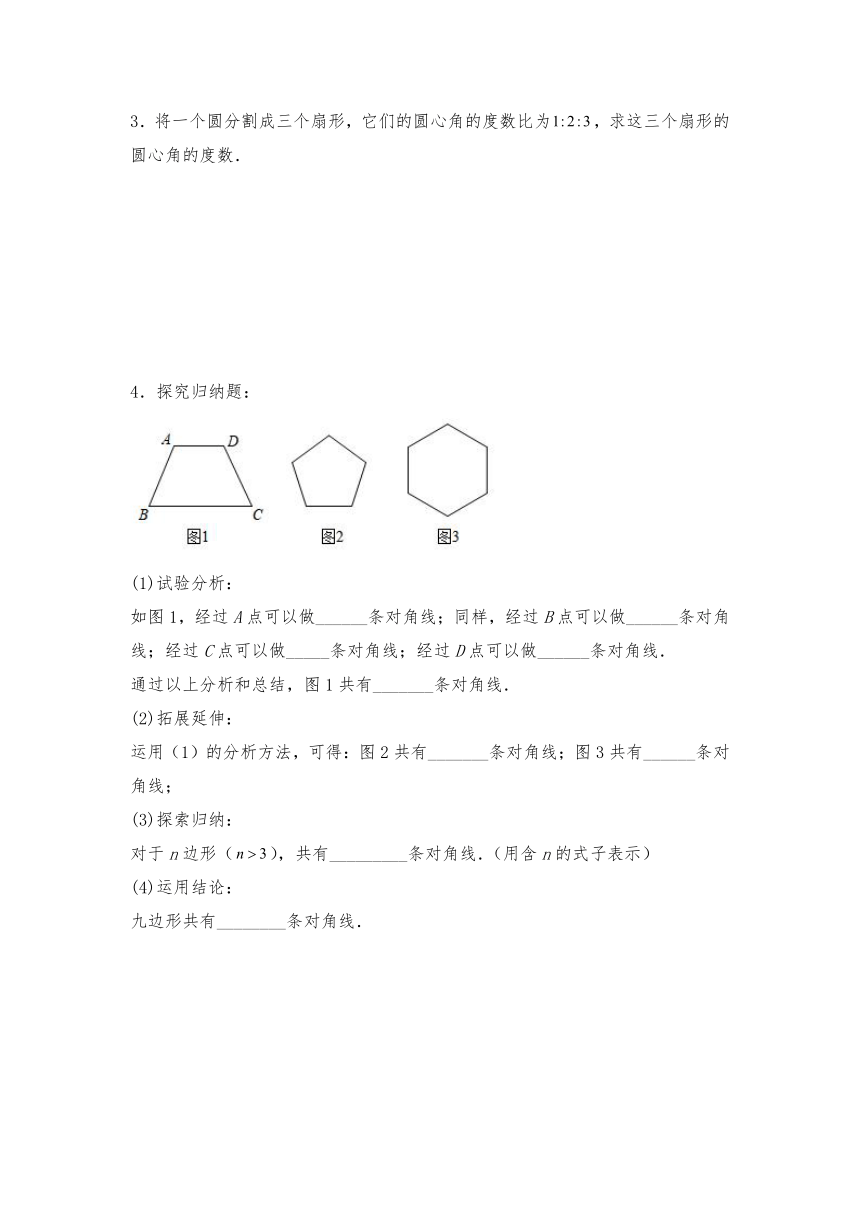
3.将一个圆分割成三个扇形,它们的圆心角的度数比为,求这三个扇形的圆心角的度数.
4.探究归纳题:
(1)试验分析:
如图1,经过A点可以做______条对角线;同样,经过B点可以做______条对角线;经过C点可以做_____条对角线;经过D点可以做______条对角线.
通过以上分析和总结,图1共有_______条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:图2共有_______条对角线;图3共有______条对角线;
(3)探索归纳:
对于n边形(),共有_________条对角线.(用含n的式子表示)
(4)运用结论:
九边形共有________条对角线.
5.如图,你能数出多少个不同的四边形?
答案
一、选择题
D.C.A.D.C.C.C.
二、填空题
1..
2.3.
3.9.
4.18.
5.140°
6.九.
7.35.
8.20°.
9.﹣1
三 、解答题
1.(1)
解:多边形的顶点数为4时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为5时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为6时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为7时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为8时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
归纳类推得:当多边形的顶点数为时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为(其中,且n为整数),
故答案为:,.
(2)
解:由题意,将问题转化为一个多边形的顶点数为76个,求这个多边形对角线的总条数与边数之和,
则,
答:他们一共通了2850次电话.
2.解:如图:
设小正方形的边长为2,E为BC中点.
则S△ABE=×1×4=2,
∴梯形ADCE的面积为:8-2=6;
则AE左侧的面积总和为:4×3+2=14,
AE右侧的面积为:4×2+6=14.
∴AE两侧的图形面积相等.
3.解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
,,,
答:这三个扇形的圆心角的度数分别为60°,120°,180°.
4.(1)
解:经过A点可以做 1条对角线;同样,经过B点可以做 1条;经过C点可以做 1条;经过D点可以做 1条对角线.
通过以上分析和总结,图1共有 2条对角线.
故答案为∶1,1,1,1,2;
(2)解∶ 运用(1)的分析方法,可得:图2共有 5条对角线;图3共有 9条对角线;
故答案为:5,9;
(3)解∶由(1),(2)可知,对于n边形(n>3),共有条对角线;
故答案为:;
(4)解:当n=9时,,
∴十边形有27对角线.
故答案为:27.
5.解:单个的四边形:一共有9个,
由2个四边形组成的四边形有6个,
由3个四边形组成的四边形有4个,
由4个四边形组成的四边形有1个,
由5个四边形组成的四边形有4个,
由6个四边形组成的四边形有2个,
由7个四边形组成的四边形有1个,
故一共有27个四边形.
一、选择题
1. 下列各组图形都是平面图形的一组是( )
A. 线段、圆、圆锥、球 B. 角、三角形、长方形、圆柱
C. 长方体、圆柱、棱锥、球 D. 圆、三角形、正方形、长方形
2. 从六边形的一个顶点出发,可引出的对角线共有( )
A. 1条 B. 2条 C. 3条 D. 4条
3. 下列正多边形中,能够铺满地面的是( )
A. 正方形 B. 正五边形 C. 正七边形 D. 正九边形
4.关于正多边形的概念,下列说法正确的是( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等或各角相等的多边形是正多边形
D.各边相等且各角相等的多边形是正多边形
5.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A. B. C. D.
6.下列说法正确的个数为( )
①连接C,D两点的线段叫两点之间的距离
②两点之间直线最短
③射线上点的个数是直线上点的个数的一半
④n边形从其中一个顶点出发连接其余各顶点,可以画出(n-3)条对角线,这些对角线把这个n边形分成了(n-2)个三角形
A.3个 B.2个 C.1个 D.0个
7.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为( )
A.2001 B.2005 C.2004 D.2006
二、填空题
1. 一个圆的直径是4cm,周长是______cm.
2. 用正六边形的瓷砖铺满地面,围绕一点拼在一起的正六边形瓷砖的块数是______块.
3.一个多边形从一个顶点引出的对角线有6条,则此多边形的边数是________ 条.
4.我们把各边相等,且各角也相等的多边形叫做正多边形,如图,边长相等的正五边形和正方形的一边重合,则________°.
5.将一个圆分成四个扇形,它们的圆心角的度数比为2:4:5:7,则最大扇形的圆心角是__.
6.从n边形的一个顶点出发,分别连接这个点与同它不相邻的各个顶点,得到7个三角形,那么这个多边形为______边形.
7.若一个多边形从一个顶点出发可以引7条对角线,则这个多边形共有______条对角线.
8.如图,将三个同样的正方形的一个顶点重合放置,那么的度数为__________.
9.已知从六边形的一个顶点出发,可以引条对角线,这些对角线可以把这个六边形分成个三角形,则______.
三、解答题
1.夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
2.如图所示是由7个完全相同的正方形拼成的图形,请你用一条直线将它分成面积相等的两部分.(在原图上作出).
3.将一个圆分割成三个扇形,它们的圆心角的度数比为,求这三个扇形的圆心角的度数.
4.探究归纳题:
(1)试验分析:
如图1,经过A点可以做______条对角线;同样,经过B点可以做______条对角线;经过C点可以做_____条对角线;经过D点可以做______条对角线.
通过以上分析和总结,图1共有_______条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:图2共有_______条对角线;图3共有______条对角线;
(3)探索归纳:
对于n边形(),共有_________条对角线.(用含n的式子表示)
(4)运用结论:
九边形共有________条对角线.
5.如图,你能数出多少个不同的四边形?
答案
一、选择题
D.C.A.D.C.C.C.
二、填空题
1..
2.3.
3.9.
4.18.
5.140°
6.九.
7.35.
8.20°.
9.﹣1
三 、解答题
1.(1)
解:多边形的顶点数为4时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为5时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为6时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为7时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
多边形的顶点数为8时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为,
归纳类推得:当多边形的顶点数为时,从一个顶点出发的对角线的条数为,多边形对角线的总条数为(其中,且n为整数),
故答案为:,.
(2)
解:由题意,将问题转化为一个多边形的顶点数为76个,求这个多边形对角线的总条数与边数之和,
则,
答:他们一共通了2850次电话.
2.解:如图:
设小正方形的边长为2,E为BC中点.
则S△ABE=×1×4=2,
∴梯形ADCE的面积为:8-2=6;
则AE左侧的面积总和为:4×3+2=14,
AE右侧的面积为:4×2+6=14.
∴AE两侧的图形面积相等.
3.解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
,,,
答:这三个扇形的圆心角的度数分别为60°,120°,180°.
4.(1)
解:经过A点可以做 1条对角线;同样,经过B点可以做 1条;经过C点可以做 1条;经过D点可以做 1条对角线.
通过以上分析和总结,图1共有 2条对角线.
故答案为∶1,1,1,1,2;
(2)解∶ 运用(1)的分析方法,可得:图2共有 5条对角线;图3共有 9条对角线;
故答案为:5,9;
(3)解∶由(1),(2)可知,对于n边形(n>3),共有条对角线;
故答案为:;
(4)解:当n=9时,,
∴十边形有27对角线.
故答案为:27.
5.解:单个的四边形:一共有9个,
由2个四边形组成的四边形有6个,
由3个四边形组成的四边形有4个,
由4个四边形组成的四边形有1个,
由5个四边形组成的四边形有4个,
由6个四边形组成的四边形有2个,
由7个四边形组成的四边形有1个,
故一共有27个四边形.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
