第二十七章 相似 单元卷(无答案)人教版数学九年级下册
文档属性
| 名称 | 第二十七章 相似 单元卷(无答案)人教版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 714.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 20:45:32 | ||
图片预览

文档简介
第二十七章 相似单元卷
一、单选题(共10小题;共20分)
1. 下列选项中的两个图形一定相似的是
A. 两个等腰三角形 B. 两个矩形
C. 两个菱形 D. 两个正方形
2. 若两个相似多边形的面积之比为 ,则这两个多边形的周长之比为
A. B. C. D.
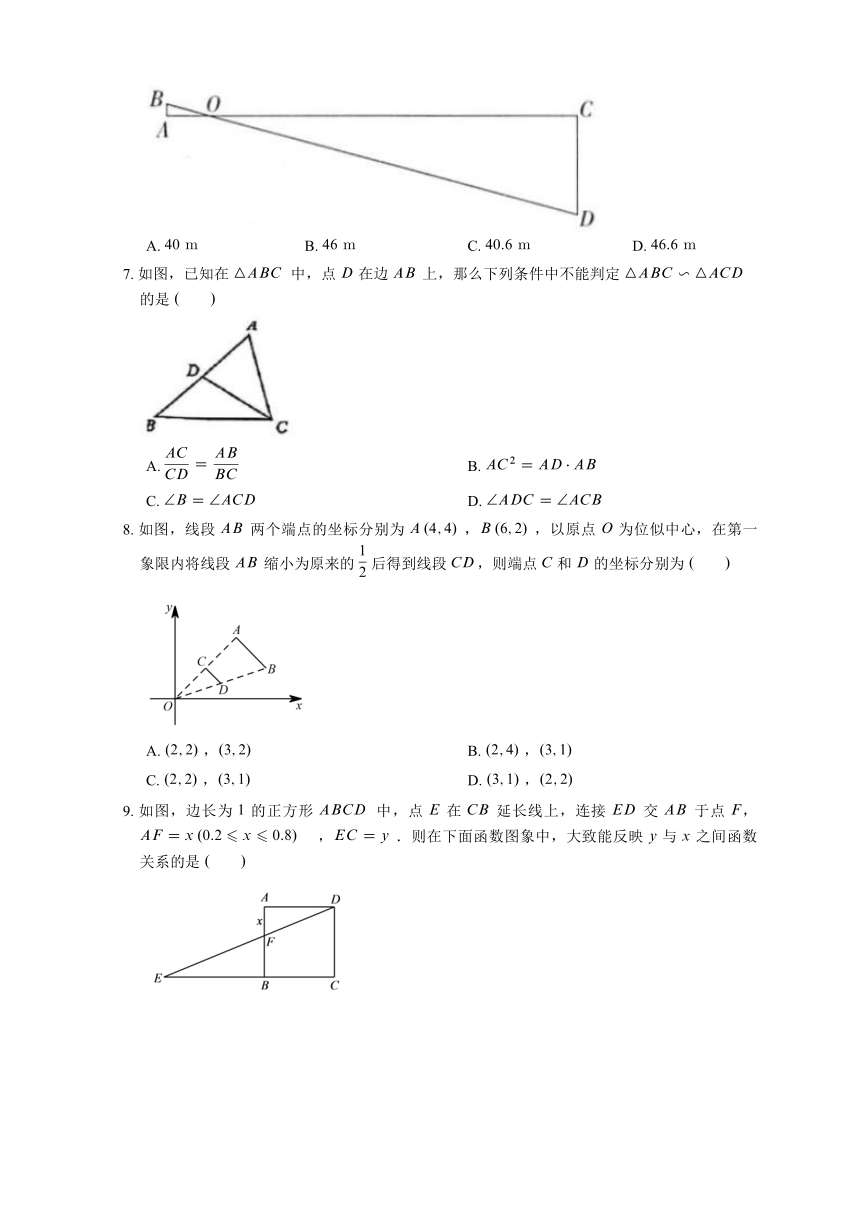
3. 某地需要开辟一条隧道,隧道 的长度无法直接测量.如图所示,在地面上取一点 ,使 到 , 两点均可直接到达,测量找到 和 的中点 ,,测得 的长为 ,则隧道 的长度为
A. B. C. D.
4. 如图,四边形 四边形 , 的度数与 的长度分别为
A. , B. , C. , D. ,
5. 如图,已知 ,,那么下列结论中,正确的是
A. B.
C. D.
6. 电视剧中炮兵用手指测量距离的方法在军事术语中叫做跳眼法,是军队使用的一种简易测距方法.如图,两眼之间的距离 ,手臂长度 ,被测物体 ,若手臂与身体垂直,被测物体与人体平行,则被测物体到人的距离 约为
A. B. C. D.
7. 如图,已知在 中,点 在边 上,那么下列条件中不能判定 的是
A. B.
C. D.
8. 如图,线段 两个端点的坐标分别为 ,,以原点 为位似中心,在第一象限内将线段 缩小为原来的 后得到线段 ,则端点 和 的坐标分别为
A. , B. ,
C. , D. ,
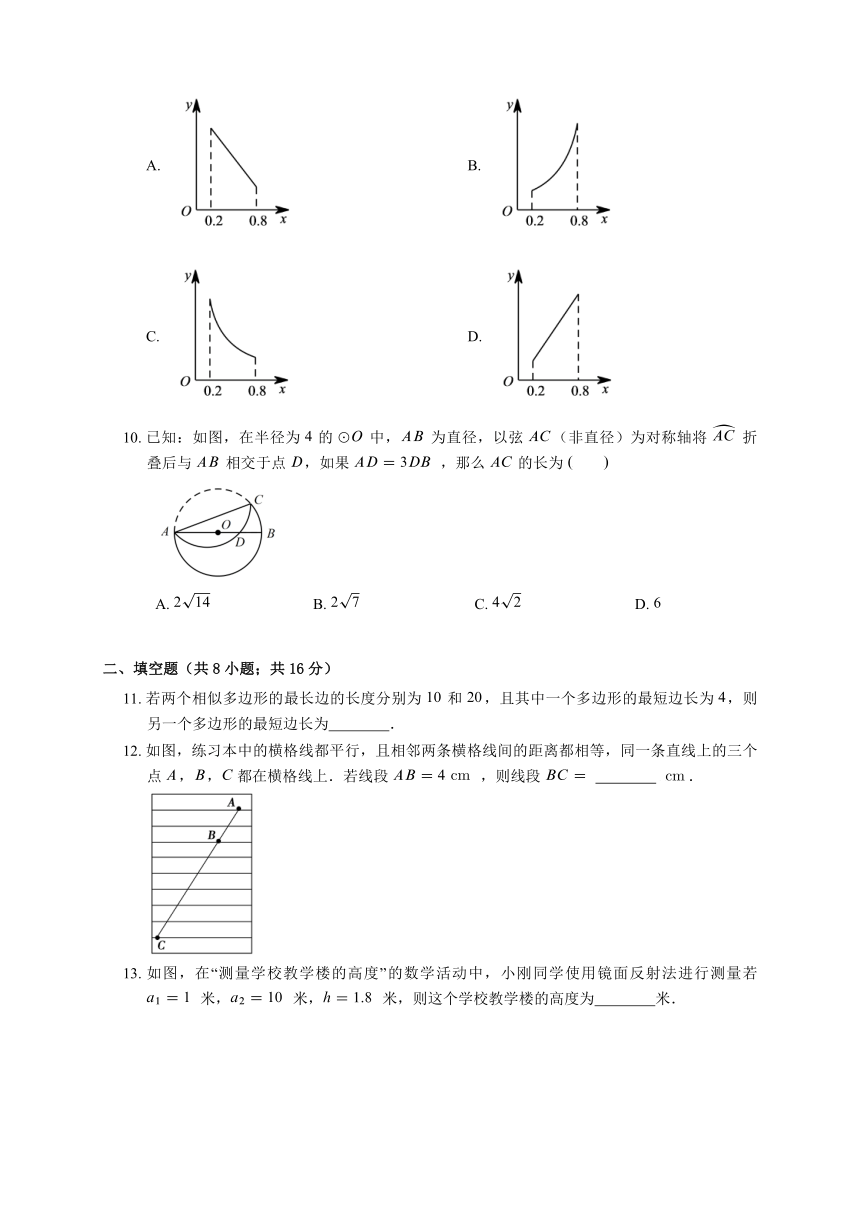
9. 如图,边长为 的正方形 中,点 在 延长线上,连接 交 于点 ,,.则在下面函数图象中,大致能反映 与 之间函数关系的是
A. B.
C. D.
10. 已知:如图,在半径为 的 中, 为直径,以弦 (非直径)为对称轴将 折叠后与 相交于点 ,如果 ,那么 的长为
A. B. C. D.
二、填空题(共8小题;共16分)
11. 若两个相似多边形的最长边的长度分别为 和 ,且其中一个多边形的最短边长为 ,则另一个多边形的最短边长为 .
12. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点 ,, 都在横格线上.若线段 ,则线段 .
13. 如图,在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量若 米, 米, 米,则这个学校教学楼的高度为 米.
14. 如图,矩形纸片 中,,,点 在 边上, 交 于点 ,若 ,则 .
15. 如图, 与 关于 轴对称,已知 ,,,若以原点 为位似中心,相似比为 作 的缩小的位似图形 ,则 的坐标是 .
16. 如图,点 , 分别在 的边 , 上,且 ,若 ,,,则 的长为 .
17. 如图,在平面直角坐标系中,正方形 的面积为 ,顶点 在 轴上,顶点 在 轴上,顶点 在双曲线 的图象上,边 交 轴于点 ,若 ,则 的值为 .
18. 如图,矩形 中,,, 在 边上,且 ,将 沿直线 折叠,得到 ,连接 ,则 的面积为 .
三、解答题(共7小题;共14分)
19. 如图,点 为平行四边形 的边 延长线上一点, 分别与 , 相交于点 ,.
(1)求证:;
(2)若 与 的面积比是 ,求 的值.
20. 如图,已知 、 均为正三角形, 、 分别在 、 上.请找出一个与 相似的三角形并证明.
21. 如图,在 中,, 沿 折叠,使得点 落在斜边 上的点 处.
(1)求证:;
(2)已知 ,,求线段 的长度.
22. 已知:如图,在四边形 中,,过点 作 ,分别交 , 于点 ,,且满足 .
(1)求证:;
(2)求证:.
23. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
24. 阅读下面材料:
小骏遇到这样一个问题:画一个和已知矩形 面积相等的正方形.
小骏发现:延长 到 ,使得 ,以 为直径作半圆,过点 作 的垂线,交半圆于点 ,以 为边作正方形 ,则正方形 即为所求.
请回答:, 和 的数量关系为 .
参考小骏思考问题的方法,解决问题:
画一个和已知平行四边形 面积相等的正方形,并写出画图的简要步骤.
25. 如图,在半径为 的圆 中,, 都是圆 的半径,且 ,点 是劣弧 上的一个动点(点 不与点 , 重合),延长 交射线 于点 .
(1)当点 为线段 中点时,求 的大小;
(2)如果设 ,,求 关于 的函数解析式,并写出定义域;
(3)当 时,点 在线段 上,且 ,点 是射线 上一点,射线 与射线 交于点 ,如果以点 ,, 为顶点的三角形与 相似,求 的值.
一、单选题(共10小题;共20分)
1. 下列选项中的两个图形一定相似的是
A. 两个等腰三角形 B. 两个矩形
C. 两个菱形 D. 两个正方形
2. 若两个相似多边形的面积之比为 ,则这两个多边形的周长之比为
A. B. C. D.
3. 某地需要开辟一条隧道,隧道 的长度无法直接测量.如图所示,在地面上取一点 ,使 到 , 两点均可直接到达,测量找到 和 的中点 ,,测得 的长为 ,则隧道 的长度为
A. B. C. D.
4. 如图,四边形 四边形 , 的度数与 的长度分别为
A. , B. , C. , D. ,
5. 如图,已知 ,,那么下列结论中,正确的是
A. B.
C. D.
6. 电视剧中炮兵用手指测量距离的方法在军事术语中叫做跳眼法,是军队使用的一种简易测距方法.如图,两眼之间的距离 ,手臂长度 ,被测物体 ,若手臂与身体垂直,被测物体与人体平行,则被测物体到人的距离 约为
A. B. C. D.
7. 如图,已知在 中,点 在边 上,那么下列条件中不能判定 的是
A. B.
C. D.
8. 如图,线段 两个端点的坐标分别为 ,,以原点 为位似中心,在第一象限内将线段 缩小为原来的 后得到线段 ,则端点 和 的坐标分别为
A. , B. ,
C. , D. ,
9. 如图,边长为 的正方形 中,点 在 延长线上,连接 交 于点 ,,.则在下面函数图象中,大致能反映 与 之间函数关系的是
A. B.
C. D.
10. 已知:如图,在半径为 的 中, 为直径,以弦 (非直径)为对称轴将 折叠后与 相交于点 ,如果 ,那么 的长为
A. B. C. D.
二、填空题(共8小题;共16分)
11. 若两个相似多边形的最长边的长度分别为 和 ,且其中一个多边形的最短边长为 ,则另一个多边形的最短边长为 .
12. 如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点 ,, 都在横格线上.若线段 ,则线段 .
13. 如图,在“测量学校教学楼的高度”的数学活动中,小刚同学使用镜面反射法进行测量若 米, 米, 米,则这个学校教学楼的高度为 米.
14. 如图,矩形纸片 中,,,点 在 边上, 交 于点 ,若 ,则 .
15. 如图, 与 关于 轴对称,已知 ,,,若以原点 为位似中心,相似比为 作 的缩小的位似图形 ,则 的坐标是 .
16. 如图,点 , 分别在 的边 , 上,且 ,若 ,,,则 的长为 .
17. 如图,在平面直角坐标系中,正方形 的面积为 ,顶点 在 轴上,顶点 在 轴上,顶点 在双曲线 的图象上,边 交 轴于点 ,若 ,则 的值为 .
18. 如图,矩形 中,,, 在 边上,且 ,将 沿直线 折叠,得到 ,连接 ,则 的面积为 .
三、解答题(共7小题;共14分)
19. 如图,点 为平行四边形 的边 延长线上一点, 分别与 , 相交于点 ,.
(1)求证:;
(2)若 与 的面积比是 ,求 的值.
20. 如图,已知 、 均为正三角形, 、 分别在 、 上.请找出一个与 相似的三角形并证明.
21. 如图,在 中,, 沿 折叠,使得点 落在斜边 上的点 处.
(1)求证:;
(2)已知 ,,求线段 的长度.
22. 已知:如图,在四边形 中,,过点 作 ,分别交 , 于点 ,,且满足 .
(1)求证:;
(2)求证:.
23. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
24. 阅读下面材料:
小骏遇到这样一个问题:画一个和已知矩形 面积相等的正方形.
小骏发现:延长 到 ,使得 ,以 为直径作半圆,过点 作 的垂线,交半圆于点 ,以 为边作正方形 ,则正方形 即为所求.
请回答:, 和 的数量关系为 .
参考小骏思考问题的方法,解决问题:
画一个和已知平行四边形 面积相等的正方形,并写出画图的简要步骤.
25. 如图,在半径为 的圆 中,, 都是圆 的半径,且 ,点 是劣弧 上的一个动点(点 不与点 , 重合),延长 交射线 于点 .
(1)当点 为线段 中点时,求 的大小;
(2)如果设 ,,求 关于 的函数解析式,并写出定义域;
(3)当 时,点 在线段 上,且 ,点 是射线 上一点,射线 与射线 交于点 ,如果以点 ,, 为顶点的三角形与 相似,求 的值.
