湖南省邵阳市新邵县2022-2023学年八年级下学期期末数学试题(含答案)
文档属性
| 名称 | 湖南省邵阳市新邵县2022-2023学年八年级下学期期末数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 481.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-01 22:29:23 | ||
图片预览



文档简介
2023年上期八年级期末质量检测
数 学
(温馨提示:本试卷共三个大题,总分120分,考试时量120分钟)
一、选择题(每小题3分,共30分)
1. 点关于原点对称的点的坐标为( )
A. B. C. D.
2. 下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列命题是假命题的是( )
A. 直角三角形斜边上的中线等于斜边的一半 B. 任意多边形的外角和等于
C. 矩形的对角线互相平分且相等 D. 四条边都相等的四边形是正方形
4. 在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
5. 如图,足球图片中的一块黑色皮块的内角和是( )
A. B. C. D.
6. 已知、,是一次函数的图象上的点.当时,、的大小关系为( )
A. B. C. D. 以上结论都有可能
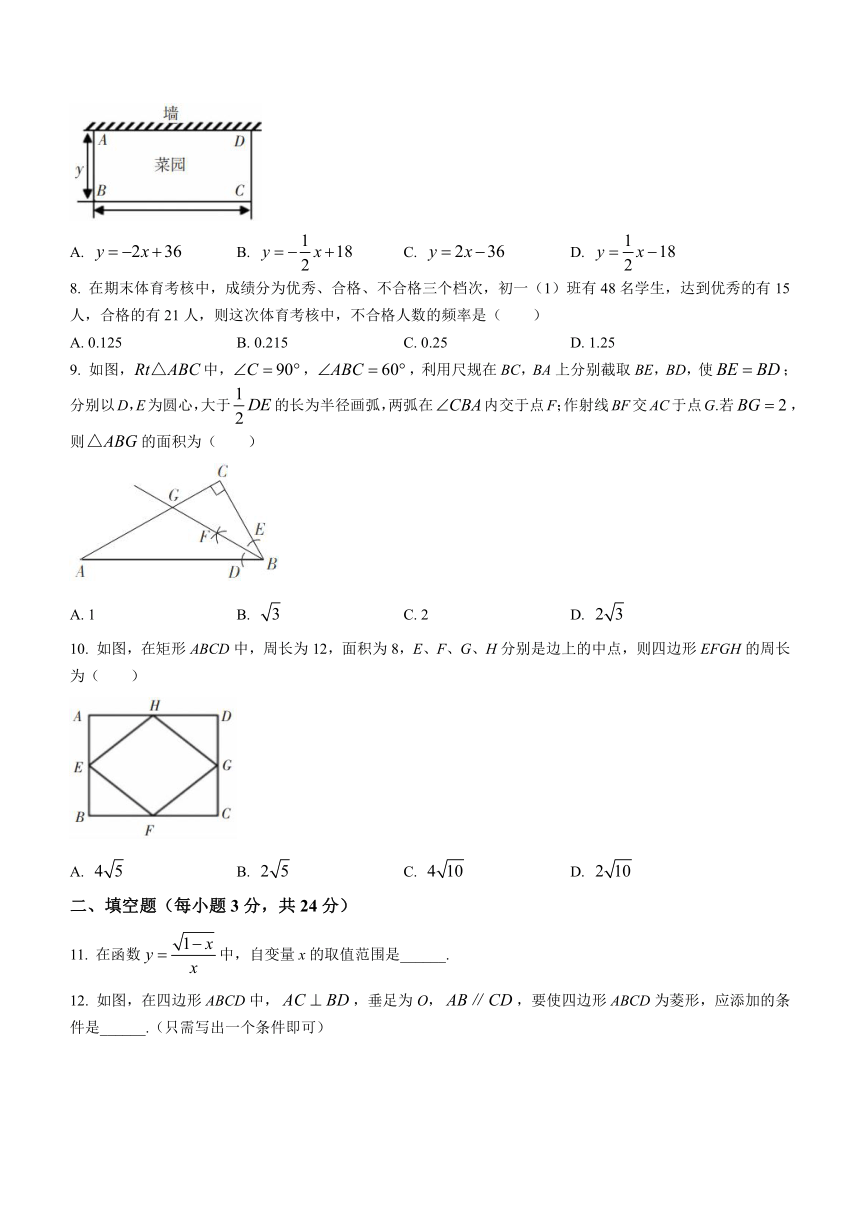
7. 某中学开设了劳动课,在校园内围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为36米,要围成的菜园是如图所示的长方形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. B. C. D.
8. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,初一(1)班有48名学生,达到优秀的有15人,合格的有21人,则这次体育考核中,不合格人数的频率是( )
A. 0.125 B. 0.215 C. 0.25 D. 1.25
9. 如图,中,,,利用尺规在BC,BA上分别截取BE,BD,使;分别以D,E为圆心,大于的长为半径画弧,两弧在内交于点F;作射线BF交AC于点G.若,则的面积为( )
A. 1 B. C. 2 D.
10. 如图,在矩形ABCD中,周长为12,面积为8,E、F、G、H分别是边上的中点,则四边形EFGH的周长为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11. 在函数中,自变量x的取值范围是______.
12. 如图,在四边形ABCD中,,垂足为O,,要使四边形ABCD为菱形,应添加的条件是______.(只需写出一个条件即可)
13. 若点是第二象限内的一点,则a的取值范围是______.
14. 已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是______.
15. 已知y与成正比例,当时,,则y与x的函数解析式是______.
16. 我们知道,四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为______.
17. 如图,等腰直角三角形纸板ABC如图放置.直角顶点C在直线l上,分别过点A、B作于点D,于点E.若,,则AB的长为______.
18. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,也被誉为“东方魔板”.19世纪传到国外,被称为“唐图”.如图是由边长为8cm的正方形ABCD薄板分为7块制作成的“七巧板”,点O是正方形的中心,点F为CD的中点,该“七巧板”中7块图形之一的正方形(阴影部分)面积为______.
三、解答题(19、20、22小题每小题8分,21、23、24小题每小题10分,25小题12分,共66分)
19. 如图,在平面直角坐标系中,三个顶点的坐标分别为,,,作出关于y轴对称的图形为.
(1)请作出;
(2)点、的坐标分别为:______、______;
(3)求的大小.
20. 如图,已知,,,BC与EF交于点O.
(1)求证:;
(2)若,求的度数.
21. 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使,测得米,在l上点D的同侧取点A、B,使,.
(1)求AB的长;
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据:,)
22. 如图,一次函数的图象过、两点,与x轴交于A点.
(1)求此一次函数的解析式;
(2)求的面积.
23. 某市各校都在深入开展劳动教育,某校为了解八年级学生一学期参加课外劳动时间(单位:h)的情况,从该校八年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数直方图.
课外劳动时间频数分布表
劳动时间分组 频数 频率
2 0.1
a 0.2
6 0.3
5 m
3 0.15
解答下列问题:
(1)频数分布表中a的值为______,m的值为______;
(2)将频数直方图补充完整;
(3)甲同学说“我参加课外劳动的时间是此次抽样调查所获得数据的中位数”,问甲同学参加课外劳动的时间在哪个范围内?
(4)若该校八年级共有学生1200人,试估计该校八年级学生一学期课外劳动时间不少于60h的人数.
24. 为全面落实乡村振兴总要求,充分发扬“为民服务孺子牛”“创新发展拓荒牛”“艰苦奋斗老黄牛”精神,某镇政府计划在该镇试种植黄桃树和桔子树共100棵.已知平均每棵果树的投入成本和产量如下表所示,且黄桃的售价为10元/kg,桔子的售价为6元/kg.设种植黄桃树x棵.
成本(元/棵) 产量(kg/棵)
黄桃树 120 30
桔子树 80 25
(1)若种植黄桃树和桔子树共获利y元,求y与x之间的函数关系式;
(2)若种植黄桃树和桔子树共获利不低于10000元,则至少要种植黄桃树多少棵?
25. 如图,在平面直角坐标系xOy,四边形OBCD是正方形,,点E是OB延长线上的一点,M是线段OB上一动点(不包括O、B),作,交的平分线于点N.
(1)直接写出C点的坐标;
(2)求证:;
(3)如图2,若,在OD上找一点P,使四边形MNCP是平行四边形,求点N的坐标.
2023年上期八年级期末质量检测数学试题(答案)
一、选择题:(本大题有10个小题,每小题3分,共30分)
1~10 BDDCB ADCBA
二、填空题:(本大题有8个小题,每小题3分,共24分)
11. 且 12. 答案不唯一 13. 14. 4
15. 16. 17. 18. 8
三、解答题:(19、20、22小题每小题8分,21、23、24小题每小题10分,26小题12分,共66分)
19. 解:(1)作图(略)………………………………………………2分
(2)、;…………………………………4分
(3)…………………………………8分
20. 解:(1)证明(略)…………………………………………………………4分
(2)………………………………………………………8分
21. 解:(1)米………………………………………5分
(2)米/秒≈43.6千米/小时>40千米/小时
∴这辆校车已超速.…………………………………………………10分
22. 解:(1)直线AB的表达式为:……………………………………4分
(2)………………………………8分
23. 解:(1)4,0. 25…………………………………………………………………4分
(2)补充频数分布直方图(略)…………………………………………6分
(3)………………………………………………………………8分
(4)(人)…………………………………………10分
24. 解:(1)y与x的函数关系式为
…………………………5分
(2)当时,,
解得.
∴至少要种植黄桃树28棵,才能获利不低于10000元.………………10分
25. 解:(1)…………………………………2分
(2)在DO上截取,
易证,
∴…………………………………7分
(3)当四边形MNCP是平行四边形时,,,
∵,∴,
又∵,,
∴,∴,
∴,∴,
作轴,垂足为点F,
可证,
∴,,
∴点N的坐标为……………………………………………12分
数 学
(温馨提示:本试卷共三个大题,总分120分,考试时量120分钟)
一、选择题(每小题3分,共30分)
1. 点关于原点对称的点的坐标为( )
A. B. C. D.
2. 下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列命题是假命题的是( )
A. 直角三角形斜边上的中线等于斜边的一半 B. 任意多边形的外角和等于
C. 矩形的对角线互相平分且相等 D. 四条边都相等的四边形是正方形
4. 在同一平面直角坐标系中,直线与相交于点,则关于x,y的方程组的解为( )
A. B. C. D.
5. 如图,足球图片中的一块黑色皮块的内角和是( )
A. B. C. D.
6. 已知、,是一次函数的图象上的点.当时,、的大小关系为( )
A. B. C. D. 以上结论都有可能
7. 某中学开设了劳动课,在校园内围一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为36米,要围成的菜园是如图所示的长方形ABCD,设BC的边长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. B. C. D.
8. 在期末体育考核中,成绩分为优秀、合格、不合格三个档次,初一(1)班有48名学生,达到优秀的有15人,合格的有21人,则这次体育考核中,不合格人数的频率是( )
A. 0.125 B. 0.215 C. 0.25 D. 1.25
9. 如图,中,,,利用尺规在BC,BA上分别截取BE,BD,使;分别以D,E为圆心,大于的长为半径画弧,两弧在内交于点F;作射线BF交AC于点G.若,则的面积为( )
A. 1 B. C. 2 D.
10. 如图,在矩形ABCD中,周长为12,面积为8,E、F、G、H分别是边上的中点,则四边形EFGH的周长为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11. 在函数中,自变量x的取值范围是______.
12. 如图,在四边形ABCD中,,垂足为O,,要使四边形ABCD为菱形,应添加的条件是______.(只需写出一个条件即可)
13. 若点是第二象限内的一点,则a的取值范围是______.
14. 已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是______.
15. 已知y与成正比例,当时,,则y与x的函数解析式是______.
16. 我们知道,四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为______.
17. 如图,等腰直角三角形纸板ABC如图放置.直角顶点C在直线l上,分别过点A、B作于点D,于点E.若,,则AB的长为______.
18. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,也被誉为“东方魔板”.19世纪传到国外,被称为“唐图”.如图是由边长为8cm的正方形ABCD薄板分为7块制作成的“七巧板”,点O是正方形的中心,点F为CD的中点,该“七巧板”中7块图形之一的正方形(阴影部分)面积为______.
三、解答题(19、20、22小题每小题8分,21、23、24小题每小题10分,25小题12分,共66分)
19. 如图,在平面直角坐标系中,三个顶点的坐标分别为,,,作出关于y轴对称的图形为.
(1)请作出;
(2)点、的坐标分别为:______、______;
(3)求的大小.
20. 如图,已知,,,BC与EF交于点O.
(1)求证:;
(2)若,求的度数.
21. 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使,测得米,在l上点D的同侧取点A、B,使,.
(1)求AB的长;
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据:,)
22. 如图,一次函数的图象过、两点,与x轴交于A点.
(1)求此一次函数的解析式;
(2)求的面积.
23. 某市各校都在深入开展劳动教育,某校为了解八年级学生一学期参加课外劳动时间(单位:h)的情况,从该校八年级随机抽查了部分学生进行问卷调查,并将调查结果绘制成如下不完整的频数分布表和频数直方图.
课外劳动时间频数分布表
劳动时间分组 频数 频率
2 0.1
a 0.2
6 0.3
5 m
3 0.15
解答下列问题:
(1)频数分布表中a的值为______,m的值为______;
(2)将频数直方图补充完整;
(3)甲同学说“我参加课外劳动的时间是此次抽样调查所获得数据的中位数”,问甲同学参加课外劳动的时间在哪个范围内?
(4)若该校八年级共有学生1200人,试估计该校八年级学生一学期课外劳动时间不少于60h的人数.
24. 为全面落实乡村振兴总要求,充分发扬“为民服务孺子牛”“创新发展拓荒牛”“艰苦奋斗老黄牛”精神,某镇政府计划在该镇试种植黄桃树和桔子树共100棵.已知平均每棵果树的投入成本和产量如下表所示,且黄桃的售价为10元/kg,桔子的售价为6元/kg.设种植黄桃树x棵.
成本(元/棵) 产量(kg/棵)
黄桃树 120 30
桔子树 80 25
(1)若种植黄桃树和桔子树共获利y元,求y与x之间的函数关系式;
(2)若种植黄桃树和桔子树共获利不低于10000元,则至少要种植黄桃树多少棵?
25. 如图,在平面直角坐标系xOy,四边形OBCD是正方形,,点E是OB延长线上的一点,M是线段OB上一动点(不包括O、B),作,交的平分线于点N.
(1)直接写出C点的坐标;
(2)求证:;
(3)如图2,若,在OD上找一点P,使四边形MNCP是平行四边形,求点N的坐标.
2023年上期八年级期末质量检测数学试题(答案)
一、选择题:(本大题有10个小题,每小题3分,共30分)
1~10 BDDCB ADCBA
二、填空题:(本大题有8个小题,每小题3分,共24分)
11. 且 12. 答案不唯一 13. 14. 4
15. 16. 17. 18. 8
三、解答题:(19、20、22小题每小题8分,21、23、24小题每小题10分,26小题12分,共66分)
19. 解:(1)作图(略)………………………………………………2分
(2)、;…………………………………4分
(3)…………………………………8分
20. 解:(1)证明(略)…………………………………………………………4分
(2)………………………………………………………8分
21. 解:(1)米………………………………………5分
(2)米/秒≈43.6千米/小时>40千米/小时
∴这辆校车已超速.…………………………………………………10分
22. 解:(1)直线AB的表达式为:……………………………………4分
(2)………………………………8分
23. 解:(1)4,0. 25…………………………………………………………………4分
(2)补充频数分布直方图(略)…………………………………………6分
(3)………………………………………………………………8分
(4)(人)…………………………………………10分
24. 解:(1)y与x的函数关系式为
…………………………5分
(2)当时,,
解得.
∴至少要种植黄桃树28棵,才能获利不低于10000元.………………10分
25. 解:(1)…………………………………2分
(2)在DO上截取,
易证,
∴…………………………………7分
(3)当四边形MNCP是平行四边形时,,,
∵,∴,
又∵,,
∴,∴,
∴,∴,
作轴,垂足为点F,
可证,
∴,,
∴点N的坐标为……………………………………………12分
同课章节目录
