北师大版八年级数学上册试题 6.4 数据的离散程度 (含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 6.4 数据的离散程度 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-02 00:00:00 | ||
图片预览




文档简介
6.4 数据的离散程度
一、选择题
1.有一组数据1、2、3、4 、5,它的方差是( )
A.2 B.10 C. D.
2.甲,乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差S甲2与S乙2的大小关系是( )
A.S甲2<S乙2 B.S甲2>S乙2 C.S甲2=S乙2 D.无法确定
3.2022年将在北京——张家口举办冬季奥运会,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 176 176 175 177 177 175
乙组 183 175 170 174 178 176
设两队队员身高的平均数依次为,,方差依次为,下列关系中正确的是( )
A. B.
C. D.
4.在第十四届全运会女排比赛中,山东女子排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,极差变大 B.中位数变小,方差变小
C.平均数变大,极差变小 D.中位数变大,方差变大
5.己知一组数据a,b,c的平均数为6,方差为4.1,那么数据,,的平均数和方差分别是( )
A.4,2.1 B.4,4.1 C.6,2.1 D.6,4.1
6.一组数据,0,3,1,的极差是( )
A.2 B.3 C.4 D.5
7.某中学青年志愿者协会的10名志愿者,一周的社区志愿服务时间如下表所示:
时间/h 2 3 4 5 6
人数 1 3 2 3 1
关于志愿者服务时间的描述正确的是( )
A.众数是6 B.平均数是4 C.中位数是3 D.方差是1
8.我们在外卖平台点单时会有点餐用的钱和外卖费6元,我们计算了点单的总额和不计算外卖费的总额的数据,则两种情况计算出的数据一样的是( )
A.平均数 B.中位数 C.众数 D.方差
9.一组数据2,4,5,6,5.对该组数据描述正确的是( )
A.平均数是4.4 B.中位数是4.5
C.众数是4 D.方差是9.2
10.一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
11.射击比赛中,某队员的10次射击成绩如图所示,则下列结论错误的是( )
A.平均数是9环 B.中位数是9环 C.众数是9环 D.方差是0.8
二、填空题
1.如图是南方某市4月7日开始未来7天日最高气温和日最低气温走势图,则在这7天中温度值的极差为________________℃.
2.已知一组数据1,5,2,4,x的平均数是3,则这组数据的方差为___________.
3.已知一个样本a,4,2,5,3,它的平均数是4,则这个样本的标准差为_____.
4.已知一组数据、、、、的方差为,则新的数据、、、、的方差是______.
5.小芳测得连续五日最低气温并整理后得出下表:
日期 一 二 三 四 五 方差 平均气温
最低气温 1 3 2 5 3
由于不小心第4日及方差两个数据被墨迹污染,这两个数据是_____.
6.甲、乙、丙、丁四名同学参加掷实心球测试,每人掷5次,他们的平均成绩恰好相同,方差分别是s甲2=0.55,s乙2=0.56,s丙2=0.52,s丁2=0.48,则这四名同学掷实心球的成绩最稳定的是_____.
三、解答题
1.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:,,,,,,.关于这组数据,
(1)众数是________,中位数是________.
(2)这组数据的平均数是________.
(3)求这组数据的方差.
2.某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 第二次 第三次 第四次
甲 9 8 8 7
乙 10 6 7 9
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩和方差;
(2)根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
3.为增强学生的防疫意识,学校进行了防疫知识宣传教育活动,为了了解活动效果,组织了测试.现从七、八年级分别任意抽取了名学生的测试成绩如下:满分为分,七、八年级学生人数分别为人和人
七年级:,,,,,,,,,
八年级:,,,,,,,,,
经整理、分析获得如下不完整的数据分析表:
年级 平均数 中位数 众数 方差
七年级 87.4 43.44
八年级 89.2
(1)填空:______,______.
(2)若成绩分以上的为良好,请估计该校七、八年级各有多少名学生的成绩为良好;
(3)根据数据分析表中所提供的统计量判断哪个年级的成绩较好?说明理由.仅需要从一个的角度说明推断的合理性
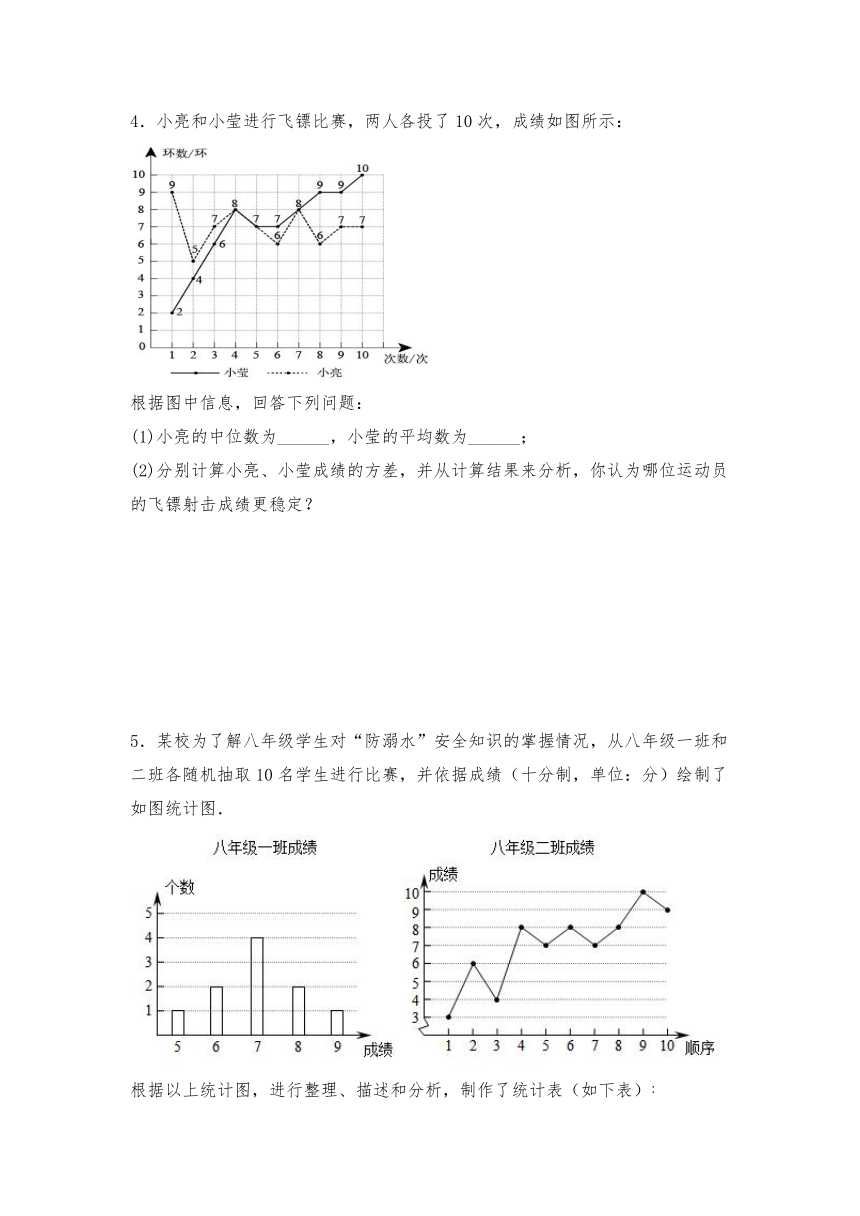
4.小亮和小莹进行飞镖比赛,两人各投了10次,成绩如图所示:
根据图中信息,回答下列问题:
(1)小亮的中位数为______,小莹的平均数为______;
(2)分别计算小亮、小莹成绩的方差,并从计算结果来分析,你认为哪位运动员的飞镖射击成绩更稳定?
5.某校为了解八年级学生对“防溺水”安全知识的掌握情况,从八年级一班和二班各随机抽取10名学生进行比赛,并依据成绩(十分制,单位:分)绘制了如图统计图.
根据以上统计图,进行整理、描述和分析,制作了统计表(如下表)
项目班级 平均分 中位数 众数 方差
八年级一班 7 7
八年级二班 7.5 4.2
温馨提示:方差计算公式:
(1)求表格中的,,,的值,并写出具体的计算过程;
(2)你认为哪个班级的成绩比较稳定?
6.某科研小组计划对某一品种的西瓜采用两种种植技术种植在选择种植技术时,该科研小组主要关心的问题是:西瓜的产量和产量的稳定性,以及西瓜的优等品率.为了解这两种种植技术种出的西瓜的质量情况,科研小组在两块自然条件相同的试验田进行对比试验,并从这两块实验田中各随机抽取20个西瓜,分别称重后,将称重的结果记录如下:
表1甲种种植技术种出的西瓜质量统计表(单位:kg)
编号 1 2 3 4 5 6 7 8 9 10
西瓜质量.(单位:kg) 3.5 4.8 5.4 4.9 4.2 5.0 4.9 4.8 5.8 4.8
编号 11 12 13 14 15 16 17 18 19 20
西瓜质量.(单位:kg) 5.0 4.8 5.2 4.9 5.1 5.0 4.8 6.0 5.7 5.0
表2乙种种植技术种出的西瓜质量统计表(单位:kg)
编号 1 2 3 4 5 6 7 8 9 10
西瓜质量.(单位:kg) 4.4 4.9 4.8 4.1 5.2 5.1 5.0 4.5 4.7 4.9
编号 11 12 13 14 15 16 17 18 19 20
西瓜质量.(单位:kg) 5.4 5.5 4.0 5.3 4.8 5.6 5.2 5.7 5.0 5.3
回答下列问题:
(1)若将质量为4.5~5.5(单位:kg)的西瓜记为优等品,完成下表:
平均数 方差 优等品西瓜个数
甲种种植技术种出的西瓜质量 4.98 0.27
乙种种植技术种出的西瓜质量 4.97 0.21 15
(2)根据以上数据,你认为该科研小组应选择哪种种植技术,并请说明理由.
7.某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、乙两位同学得分的折线图:
b.丙同学得分:
10,10,10,9,9,8,3,9,8,10
c.甲、乙、丙三位同学得分的平均数:
同学 甲 乙 丙
平均数 8.6 8.6 m
根据以上信息,回答下列问题:
(1)求表中m的值;
(2)在参加比赛的同学中,如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致.据此推断:甲、乙两位同学中,评委对_________的评价更一致(填“甲”或“乙”);
(3)如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀.据此推断:在甲、乙、丙三位同学中,表现最优秀的是_________(填“甲”“乙”或“丙”).
8.为庆祝中国共产主义青年团成立100周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示:
众数 中位数 方差
八年级竞赛成绩 7 8 1.88
九年级竞赛成绩 a 8 b
(1)你能用成绩的平均数判断哪个年级的成绩比较好吗?通过计算说明;
(2)请根据图表中的信息,回答下列问题.
①表中的______,______;
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖?
(3)若规定成绩10分获一等奖,9分获二等奖,8分获三等奖,则哪个年级的获奖率高?
9.为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
答案
一、选择题
A.B.A.B.B.D.B.D.A.B.D
二、填空题
1.15. 2.2. 3.. 4.4.8 5.4和2. 6.丁.
三、解答题
1.(1)
解:在这组数据中,11出现的次数最多,
所以众数是11,
将这组数据按从小到大进行排序为,
所以中位数是11,
故答案为:11,11.
(2)
解:这组数据的平均数是,
故答案为:12.
(3)
解:这组数据的方差为,
答:这组数据的方差为.
2.(1)
解:甲的平均成绩是:(9+8+8+7)÷4=8,
甲的方差是:=,
乙的平均成绩是:(10+6+7+9)÷4=8,
乙的方差是:.
(2)
解:推荐甲参加省比赛更合适.
理由:两人的平均成绩相等,说明实力相当;但是甲的测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加省比赛更合适.
3.(1)
解:由七年级的测试成绩可得, 众数a=81
把八年级的测试成绩排序为:,,,,,,,,,,
则八年级的中位数
故答案为:,;
(2)
该校七年级学生成绩良好的比例为
∴ 成绩良好的人数为
该校八年级学生成绩良好的比例为
∴ 成绩良好的人数为
故该校七年级名学生的成绩为良好,八年级名学生的成绩为良好
(3)
七年级的成绩较好,理由如下:
七年级的平均数比八年级的平均数高;
七年级的方差较小,成绩稳定.
4.(1)
解:小亮的飞镖射击成绩由小到大排列为:5,6,6,7,7,7,7,8,8,9,
位于第5、第6位的数分别是7,7,
所以小亮的中位数是(7+7)÷2=7;
小莹的平均数(2+4+6+8+7+7+8+9+9+10)=7,
故答案为:7,7;
(2)
小亮的平均数(5+6+6+7+7+7+7+8+8+9)=7,
S2小亮[(5﹣7)2+2×(6﹣7)2+4×(7﹣7)2+(9﹣7)2+2×(8﹣7)2]=1.2,
S2小莹[(2﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+2×(9﹣7)2+2×(8﹣7)2+(10﹣7)2]=5.4,
∵S2小亮<S2小莹,
∴小亮的飞镖射击成绩更稳定.
5.(1)
解:根据题意可知:
八年一班10名学生成绩:
5,6,6,7,7,7,7,8,8,9;
所以,
.
八年二班10名学生成绩:
3,4,6,7,7,8,8,8,9,10.
所以,
;
(2)
解:,
八年一班学生成绩比较稳定.
6.(1)
解:甲种种植技术种岀的西瓜优等品西瓜个数是15,
故答案为:15.
(2)
该科研小组应选择乙种种植技术
因为甲、乙优等品西瓜个数相同,虽然甲种种植技术种出的西瓜平均数略高,但乙种种植技术种出的西瓜的质量比较稳定,
应选择乙种种植技术.
7.(1)
解:丙的平均数:,
则.
(2)
,
,
,
∴甲、乙两位同学中,评委对甲的评价更一致,
故答案为:甲.
(3)
由题意得,去掉一个最高分和一个最低分后的平均分为:
甲:,
乙:,
丙:,
∵去掉一个最高分和一个最低分后丙的平均分最高,
因此最优秀的是丙,
故答案为:丙.
8.(1)
解:无法判断,计算如下:
由题意得:
八年级成绩的平均数是:(6×7+7×15+8×10+9×7+10×11)÷50=8(分),
九年级成绩的平均数是:(6×8+7×9+8×14+9×13+10×6)÷50=8(分),
故用平均数无法判定哪个年级的成绩比较好;
(2)
解:①九年级竞赛成绩中8分出现的次数最多,故众数a=8分;
九年级竞赛成绩的方差为:
,
故答案为:8;1.56;
②如果从众数角度看,八年级的众数为7分,九年级的众数为8分,所以应该给九年级颁奖;
如果从方差角度看,八年级的方差为1.88,九年级的方差为1.56,又因为两个年级的平均数相同,九年级的成绩的波动小,所以应该给九年级颁奖,
故如果分别从众数和方差两个角度来分析,应该给九年级颁奖;
(3)
解:八年级的获奖率为:(10+7+11)÷50=56%,
九年级的获奖率为:(14+13+6)÷50=66%,
∵66%>56%,
∴九年级的获奖率高.
9.(1)解:由题意知,(1)班和(2)班人数相等,为:5+10+19+12+4=50(人),∴(2)班学生中测试成绩为10分的人数为:50×(1﹣28%﹣22%﹣24%﹣14%)=6(人),答:(2)班学生中测试成绩为10分的人数是6人;
(2)由题意知:a==8;∵9分占总体的百分比为28%是最大的,∴9分的人数是最多的,∴众数为9分,即b=9;由题意可知,(1)班的成绩按照从小到大排列后,中间两个数都是8,∴c==8;答:a,b,c的值分别为8,9,8;
(3)∵(1)班的方差为1.16,(2)班的方差为1.56,且1.16<1.56,∴根据方差越小,数据分布越均匀可知(1)班成绩更均匀.
一、选择题
1.有一组数据1、2、3、4 、5,它的方差是( )
A.2 B.10 C. D.
2.甲,乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差S甲2与S乙2的大小关系是( )
A.S甲2<S乙2 B.S甲2>S乙2 C.S甲2=S乙2 D.无法确定
3.2022年将在北京——张家口举办冬季奥运会,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 队员2 队员3 队员4 队员5 队员6
甲组 176 176 175 177 177 175
乙组 183 175 170 174 178 176
设两队队员身高的平均数依次为,,方差依次为,下列关系中正确的是( )
A. B.
C. D.
4.在第十四届全运会女排比赛中,山东女子排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,极差变大 B.中位数变小,方差变小
C.平均数变大,极差变小 D.中位数变大,方差变大
5.己知一组数据a,b,c的平均数为6,方差为4.1,那么数据,,的平均数和方差分别是( )
A.4,2.1 B.4,4.1 C.6,2.1 D.6,4.1
6.一组数据,0,3,1,的极差是( )
A.2 B.3 C.4 D.5
7.某中学青年志愿者协会的10名志愿者,一周的社区志愿服务时间如下表所示:
时间/h 2 3 4 5 6
人数 1 3 2 3 1
关于志愿者服务时间的描述正确的是( )
A.众数是6 B.平均数是4 C.中位数是3 D.方差是1
8.我们在外卖平台点单时会有点餐用的钱和外卖费6元,我们计算了点单的总额和不计算外卖费的总额的数据,则两种情况计算出的数据一样的是( )
A.平均数 B.中位数 C.众数 D.方差
9.一组数据2,4,5,6,5.对该组数据描述正确的是( )
A.平均数是4.4 B.中位数是4.5
C.众数是4 D.方差是9.2
10.一组数据:3,4,4,6,若添加一个数据6,则不发生变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
11.射击比赛中,某队员的10次射击成绩如图所示,则下列结论错误的是( )
A.平均数是9环 B.中位数是9环 C.众数是9环 D.方差是0.8
二、填空题
1.如图是南方某市4月7日开始未来7天日最高气温和日最低气温走势图,则在这7天中温度值的极差为________________℃.
2.已知一组数据1,5,2,4,x的平均数是3,则这组数据的方差为___________.
3.已知一个样本a,4,2,5,3,它的平均数是4,则这个样本的标准差为_____.
4.已知一组数据、、、、的方差为,则新的数据、、、、的方差是______.
5.小芳测得连续五日最低气温并整理后得出下表:
日期 一 二 三 四 五 方差 平均气温
最低气温 1 3 2 5 3
由于不小心第4日及方差两个数据被墨迹污染,这两个数据是_____.
6.甲、乙、丙、丁四名同学参加掷实心球测试,每人掷5次,他们的平均成绩恰好相同,方差分别是s甲2=0.55,s乙2=0.56,s丙2=0.52,s丁2=0.48,则这四名同学掷实心球的成绩最稳定的是_____.
三、解答题
1.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:,,,,,,.关于这组数据,
(1)众数是________,中位数是________.
(2)这组数据的平均数是________.
(3)求这组数据的方差.
2.某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了四次测试,测试成绩如表(单位:环):
第一次 第二次 第三次 第四次
甲 9 8 8 7
乙 10 6 7 9
(1)根据表格中的数据,分别计算甲、乙两名运动员的平均成绩和方差;
(2)根据计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
3.为增强学生的防疫意识,学校进行了防疫知识宣传教育活动,为了了解活动效果,组织了测试.现从七、八年级分别任意抽取了名学生的测试成绩如下:满分为分,七、八年级学生人数分别为人和人
七年级:,,,,,,,,,
八年级:,,,,,,,,,
经整理、分析获得如下不完整的数据分析表:
年级 平均数 中位数 众数 方差
七年级 87.4 43.44
八年级 89.2
(1)填空:______,______.
(2)若成绩分以上的为良好,请估计该校七、八年级各有多少名学生的成绩为良好;
(3)根据数据分析表中所提供的统计量判断哪个年级的成绩较好?说明理由.仅需要从一个的角度说明推断的合理性
4.小亮和小莹进行飞镖比赛,两人各投了10次,成绩如图所示:
根据图中信息,回答下列问题:
(1)小亮的中位数为______,小莹的平均数为______;
(2)分别计算小亮、小莹成绩的方差,并从计算结果来分析,你认为哪位运动员的飞镖射击成绩更稳定?
5.某校为了解八年级学生对“防溺水”安全知识的掌握情况,从八年级一班和二班各随机抽取10名学生进行比赛,并依据成绩(十分制,单位:分)绘制了如图统计图.
根据以上统计图,进行整理、描述和分析,制作了统计表(如下表)
项目班级 平均分 中位数 众数 方差
八年级一班 7 7
八年级二班 7.5 4.2
温馨提示:方差计算公式:
(1)求表格中的,,,的值,并写出具体的计算过程;
(2)你认为哪个班级的成绩比较稳定?
6.某科研小组计划对某一品种的西瓜采用两种种植技术种植在选择种植技术时,该科研小组主要关心的问题是:西瓜的产量和产量的稳定性,以及西瓜的优等品率.为了解这两种种植技术种出的西瓜的质量情况,科研小组在两块自然条件相同的试验田进行对比试验,并从这两块实验田中各随机抽取20个西瓜,分别称重后,将称重的结果记录如下:
表1甲种种植技术种出的西瓜质量统计表(单位:kg)
编号 1 2 3 4 5 6 7 8 9 10
西瓜质量.(单位:kg) 3.5 4.8 5.4 4.9 4.2 5.0 4.9 4.8 5.8 4.8
编号 11 12 13 14 15 16 17 18 19 20
西瓜质量.(单位:kg) 5.0 4.8 5.2 4.9 5.1 5.0 4.8 6.0 5.7 5.0
表2乙种种植技术种出的西瓜质量统计表(单位:kg)
编号 1 2 3 4 5 6 7 8 9 10
西瓜质量.(单位:kg) 4.4 4.9 4.8 4.1 5.2 5.1 5.0 4.5 4.7 4.9
编号 11 12 13 14 15 16 17 18 19 20
西瓜质量.(单位:kg) 5.4 5.5 4.0 5.3 4.8 5.6 5.2 5.7 5.0 5.3
回答下列问题:
(1)若将质量为4.5~5.5(单位:kg)的西瓜记为优等品,完成下表:
平均数 方差 优等品西瓜个数
甲种种植技术种出的西瓜质量 4.98 0.27
乙种种植技术种出的西瓜质量 4.97 0.21 15
(2)根据以上数据,你认为该科研小组应选择哪种种植技术,并请说明理由.
7.某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
a.甲、乙两位同学得分的折线图:
b.丙同学得分:
10,10,10,9,9,8,3,9,8,10
c.甲、乙、丙三位同学得分的平均数:
同学 甲 乙 丙
平均数 8.6 8.6 m
根据以上信息,回答下列问题:
(1)求表中m的值;
(2)在参加比赛的同学中,如果某同学得分的10个数据的方差越小,则认为评委对该同学演唱的评价越一致.据此推断:甲、乙两位同学中,评委对_________的评价更一致(填“甲”或“乙”);
(3)如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀.据此推断:在甲、乙、丙三位同学中,表现最优秀的是_________(填“甲”“乙”或“丙”).
8.为庆祝中国共产主义青年团成立100周年,学校团委在八、九年级各抽取50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示:
众数 中位数 方差
八年级竞赛成绩 7 8 1.88
九年级竞赛成绩 a 8 b
(1)你能用成绩的平均数判断哪个年级的成绩比较好吗?通过计算说明;
(2)请根据图表中的信息,回答下列问题.
①表中的______,______;
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖?
(3)若规定成绩10分获一等奖,9分获二等奖,8分获三等奖,则哪个年级的获奖率高?
9.为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
答案
一、选择题
A.B.A.B.B.D.B.D.A.B.D
二、填空题
1.15. 2.2. 3.. 4.4.8 5.4和2. 6.丁.
三、解答题
1.(1)
解:在这组数据中,11出现的次数最多,
所以众数是11,
将这组数据按从小到大进行排序为,
所以中位数是11,
故答案为:11,11.
(2)
解:这组数据的平均数是,
故答案为:12.
(3)
解:这组数据的方差为,
答:这组数据的方差为.
2.(1)
解:甲的平均成绩是:(9+8+8+7)÷4=8,
甲的方差是:=,
乙的平均成绩是:(10+6+7+9)÷4=8,
乙的方差是:.
(2)
解:推荐甲参加省比赛更合适.
理由:两人的平均成绩相等,说明实力相当;但是甲的测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加省比赛更合适.
3.(1)
解:由七年级的测试成绩可得, 众数a=81
把八年级的测试成绩排序为:,,,,,,,,,,
则八年级的中位数
故答案为:,;
(2)
该校七年级学生成绩良好的比例为
∴ 成绩良好的人数为
该校八年级学生成绩良好的比例为
∴ 成绩良好的人数为
故该校七年级名学生的成绩为良好,八年级名学生的成绩为良好
(3)
七年级的成绩较好,理由如下:
七年级的平均数比八年级的平均数高;
七年级的方差较小,成绩稳定.
4.(1)
解:小亮的飞镖射击成绩由小到大排列为:5,6,6,7,7,7,7,8,8,9,
位于第5、第6位的数分别是7,7,
所以小亮的中位数是(7+7)÷2=7;
小莹的平均数(2+4+6+8+7+7+8+9+9+10)=7,
故答案为:7,7;
(2)
小亮的平均数(5+6+6+7+7+7+7+8+8+9)=7,
S2小亮[(5﹣7)2+2×(6﹣7)2+4×(7﹣7)2+(9﹣7)2+2×(8﹣7)2]=1.2,
S2小莹[(2﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+2×(9﹣7)2+2×(8﹣7)2+(10﹣7)2]=5.4,
∵S2小亮<S2小莹,
∴小亮的飞镖射击成绩更稳定.
5.(1)
解:根据题意可知:
八年一班10名学生成绩:
5,6,6,7,7,7,7,8,8,9;
所以,
.
八年二班10名学生成绩:
3,4,6,7,7,8,8,8,9,10.
所以,
;
(2)
解:,
八年一班学生成绩比较稳定.
6.(1)
解:甲种种植技术种岀的西瓜优等品西瓜个数是15,
故答案为:15.
(2)
该科研小组应选择乙种种植技术
因为甲、乙优等品西瓜个数相同,虽然甲种种植技术种出的西瓜平均数略高,但乙种种植技术种出的西瓜的质量比较稳定,
应选择乙种种植技术.
7.(1)
解:丙的平均数:,
则.
(2)
,
,
,
∴甲、乙两位同学中,评委对甲的评价更一致,
故答案为:甲.
(3)
由题意得,去掉一个最高分和一个最低分后的平均分为:
甲:,
乙:,
丙:,
∵去掉一个最高分和一个最低分后丙的平均分最高,
因此最优秀的是丙,
故答案为:丙.
8.(1)
解:无法判断,计算如下:
由题意得:
八年级成绩的平均数是:(6×7+7×15+8×10+9×7+10×11)÷50=8(分),
九年级成绩的平均数是:(6×8+7×9+8×14+9×13+10×6)÷50=8(分),
故用平均数无法判定哪个年级的成绩比较好;
(2)
解:①九年级竞赛成绩中8分出现的次数最多,故众数a=8分;
九年级竞赛成绩的方差为:
,
故答案为:8;1.56;
②如果从众数角度看,八年级的众数为7分,九年级的众数为8分,所以应该给九年级颁奖;
如果从方差角度看,八年级的方差为1.88,九年级的方差为1.56,又因为两个年级的平均数相同,九年级的成绩的波动小,所以应该给九年级颁奖,
故如果分别从众数和方差两个角度来分析,应该给九年级颁奖;
(3)
解:八年级的获奖率为:(10+7+11)÷50=56%,
九年级的获奖率为:(14+13+6)÷50=66%,
∵66%>56%,
∴九年级的获奖率高.
9.(1)解:由题意知,(1)班和(2)班人数相等,为:5+10+19+12+4=50(人),∴(2)班学生中测试成绩为10分的人数为:50×(1﹣28%﹣22%﹣24%﹣14%)=6(人),答:(2)班学生中测试成绩为10分的人数是6人;
(2)由题意知:a==8;∵9分占总体的百分比为28%是最大的,∴9分的人数是最多的,∴众数为9分,即b=9;由题意可知,(1)班的成绩按照从小到大排列后,中间两个数都是8,∴c==8;答:a,b,c的值分别为8,9,8;
(3)∵(1)班的方差为1.16,(2)班的方差为1.56,且1.16<1.56,∴根据方差越小,数据分布越均匀可知(1)班成绩更均匀.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
