1.1 菱形的性质与判定(第三课时 菱形的性质与判定综合应用)课件(共16张PPT)
文档属性
| 名称 | 1.1 菱形的性质与判定(第三课时 菱形的性质与判定综合应用)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
1.1 菱形的性质与判定
第一章 特殊平行四边形
第三课时 菱形的性质与判定综合应用
学习目标
1)掌握菱形面积的特殊计算方法。
2)灵活运用菱形的性质定理与判定定理解决相关问题。
重点
掌握菱形面积的特殊计算方法。
难点
灵活运用菱形的性质定理与判定定理解决相关问题。
菱形的性质:
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
边
角
对角线
两条对角线互相垂直平分
每一条对角线平分一组对角
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
四条边相等的四边形是菱形。
菱形的判定方法:
(1)定义法:
(2)判定定理1:
(3)判定定理2:
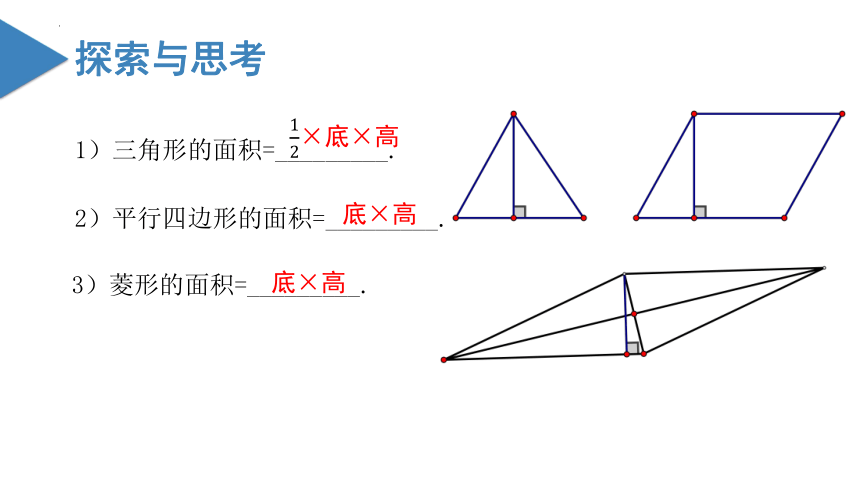
2)平行四边形的面积=_________.
×底×高
1)三角形的面积=_________.
底×高
3)菱形的面积=_________.
底×高
菱形是特殊的平行四边形,能否利用它的性质计算菱形ABCD的面积
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
=AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
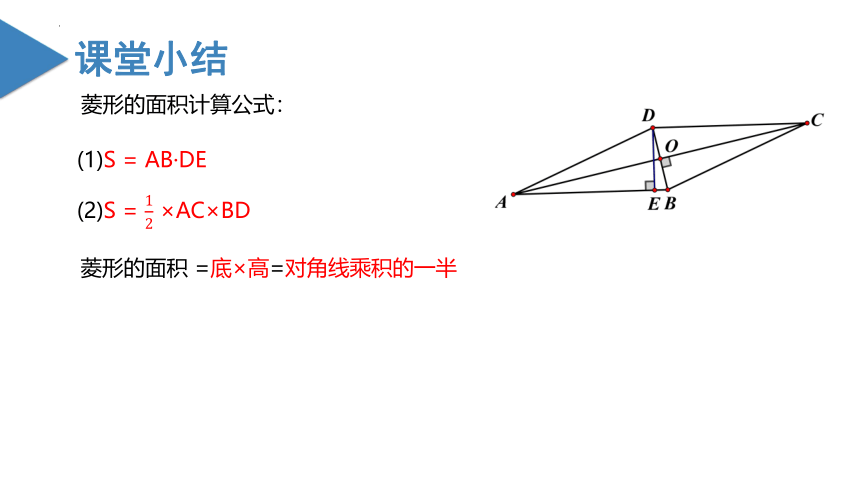
(1)S = AB·DE
菱形的面积计算公式:
菱形的面积 =底×高=对角线乘积的一半
(2)S = ×AC×BD
如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
A
B
C
D
O
解:∵花坛ABCD是菱形
∴AC⊥BD,∠ABO= ∠ABC=30°
在Rt ABO中,AO= AB=10
∴BO==10 m
AC=2AO=20 m,BD=2BO=10≈34.64 m
S菱形ABCD =4S△ABO = AC·BD =200≈316.4 ㎡
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
A.18 B.18 C.36 D.36
【解析】
过点A作AE⊥BC于E
∵在菱形ABCD中,AB=6,∠ABD=30°,
∴∠BAE=30°,
∵AE⊥BC,
∴AE=,
∴菱形ABCD的面积是=,故选B.
E
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB=,
∵菱形ABCD的面积=AB DE=AC BD=×8×6=24,
∴DE==4.8 故选B.
在菱形ABCD中,∠ABC∠BAD的度数比为1:2,周长是8cm。
求:1)两条对角线的长度;2)菱形的面积。
A
B
C
D
解:1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=60°,∠ABO=30°
∴△ABC是等边三角形。则AC=AB
∵菱形ABCD的周长是8cm.∴AB=AC=2cm
∴在Rt ABO中,AO= AB=1 cm
∴BO== cm∴AC=2 cm,BD= cm
重叠部分是:平行四边形
理由:∵AB∥ CD,AD∥BC
∴四边形ABCD是平行四边形
A
B
C
D
如图两张不等宽的纸条交叉重叠在一起,重叠的部分是什么图形?
A
B
C
D
菱形
∵SABCD =BC×AE=CD×AF
而AE=AF
∴ BC=CD
∟
∟
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
E
F
如图,在菱形中,对角线、相交于点,,,过作的平行线交的延长线于点,则的面积为( )
A.22 B.24 C.48 D.44
【详解】
解:∵AD∥BE,AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE=6,
在RT△BCO中,BO=,即可得BD=8,
又∵BE=BC+CE=BC+AD=10,
∴△BDE是直角三角形,
∴S△BDE=.
故答案为B.
如图,菱形的面积为,正方形AECF的面积为,则菱形的边长为_______.
【详解】
因为正方形AECF的面积为50cm2,
所以,
因为菱形ABCD的面积为120cm2,
所以,
所以菱形的边长=.
故答案为:13.
【解析】
由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长=cm.
故答案为.
已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
方法总结:
1.面积求法:两种。
2.边、线求法:利用4个直角三角形,知二求一。
3.角:知一角而知全部。
4.关注30°、60°、120°的特殊性。
1.1 菱形的性质与判定
第一章 特殊平行四边形
第三课时 菱形的性质与判定综合应用
学习目标
1)掌握菱形面积的特殊计算方法。
2)灵活运用菱形的性质定理与判定定理解决相关问题。
重点
掌握菱形面积的特殊计算方法。
难点
灵活运用菱形的性质定理与判定定理解决相关问题。
菱形的性质:
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
边
角
对角线
两条对角线互相垂直平分
每一条对角线平分一组对角
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
四条边相等的四边形是菱形。
菱形的判定方法:
(1)定义法:
(2)判定定理1:
(3)判定定理2:
2)平行四边形的面积=_________.
×底×高
1)三角形的面积=_________.
底×高
3)菱形的面积=_________.
底×高
菱形是特殊的平行四边形,能否利用它的性质计算菱形ABCD的面积
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
=AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
(1)S = AB·DE
菱形的面积计算公式:
菱形的面积 =底×高=对角线乘积的一半
(2)S = ×AC×BD
如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
A
B
C
D
O
解:∵花坛ABCD是菱形
∴AC⊥BD,∠ABO= ∠ABC=30°
在Rt ABO中,AO= AB=10
∴BO==10 m
AC=2AO=20 m,BD=2BO=10≈34.64 m
S菱形ABCD =4S△ABO = AC·BD =200≈316.4 ㎡
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
A.18 B.18 C.36 D.36
【解析】
过点A作AE⊥BC于E
∵在菱形ABCD中,AB=6,∠ABD=30°,
∴∠BAE=30°,
∵AE⊥BC,
∴AE=,
∴菱形ABCD的面积是=,故选B.
E
如图,已知菱形的两条对角线分别为6cm和8cm,则这个菱形的高DE为( )
A.2.4cm B.4.8cm C.5cm D.9.6cm
【详解】
解:∵四边形ABCD是菱形,
∴OA=AC=4,OB=BD=3,AC⊥BD,
∴AB=,
∵菱形ABCD的面积=AB DE=AC BD=×8×6=24,
∴DE==4.8 故选B.
在菱形ABCD中,∠ABC∠BAD的度数比为1:2,周长是8cm。
求:1)两条对角线的长度;2)菱形的面积。
A
B
C
D
解:1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AD∥BC,
∴∠ABC+∠BAD=180
∵∠ABC与∠BAD的度数比为1:2,
∴∠ABC=60°,∠ABO=30°
∴△ABC是等边三角形。则AC=AB
∵菱形ABCD的周长是8cm.∴AB=AC=2cm
∴在Rt ABO中,AO= AB=1 cm
∴BO== cm∴AC=2 cm,BD= cm
重叠部分是:平行四边形
理由:∵AB∥ CD,AD∥BC
∴四边形ABCD是平行四边形
A
B
C
D
如图两张不等宽的纸条交叉重叠在一起,重叠的部分是什么图形?
A
B
C
D
菱形
∵SABCD =BC×AE=CD×AF
而AE=AF
∴ BC=CD
∟
∟
如图两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是什么图形?为什么?
E
F
如图,在菱形中,对角线、相交于点,,,过作的平行线交的延长线于点,则的面积为( )
A.22 B.24 C.48 D.44
【详解】
解:∵AD∥BE,AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE=6,
在RT△BCO中,BO=,即可得BD=8,
又∵BE=BC+CE=BC+AD=10,
∴△BDE是直角三角形,
∴S△BDE=.
故答案为B.
如图,菱形的面积为,正方形AECF的面积为,则菱形的边长为_______.
【详解】
因为正方形AECF的面积为50cm2,
所以,
因为菱形ABCD的面积为120cm2,
所以,
所以菱形的边长=.
故答案为:13.
【解析】
由菱形的面积公式,可得另一对角线长12×2÷4=6,
∵菱形的对角线互相垂直平分,
根据勾股定理可得菱形的边长=cm.
故答案为.
已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是______cm.
方法总结:
1.面积求法:两种。
2.边、线求法:利用4个直角三角形,知二求一。
3.角:知一角而知全部。
4.关注30°、60°、120°的特殊性。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
