11.1.1 三角形的边 同步课件 (共33张PPT)
文档属性
| 名称 | 11.1.1 三角形的边 同步课件 (共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 42.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 18:23:59 | ||
图片预览







文档简介
(共33张PPT)
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
11.1.1
三角形的边
情景导入
猜谜:
形状似座山,
稳定性能坚.
三竿首尾连,
学问不简单.
情景导入
生活中的三角形
从古埃及的金字塔到现代大桥,都有什么样的形象?
在我们的生活中有没有这样的形象呢?试举例.
情景导入
生活中的三角形
新知探究
思考:观察三角形的形成过程,说一说什么叫三角形.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
三角形
要点
不在同一条直线上
要点1
三条线段
要点2
首尾顺次相接
要点3
典例精析
例1
下列图形是三角形吗?
不是
不是
是
不是
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
新知探究
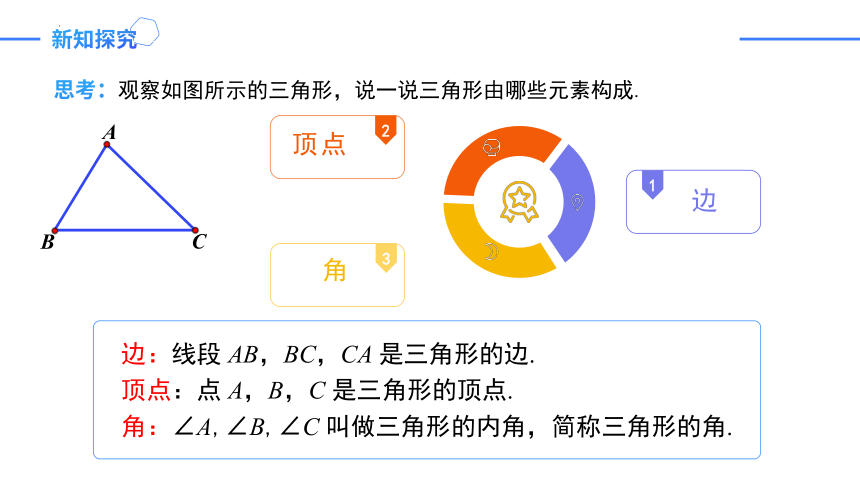
思考:观察如图所示的三角形,说一说三角形由哪些元素构成.
A
B
C
边
顶点
角
1
2
3
边:线段 AB,BC,CA 是三角形的边.
顶点:点 A,B,C 是三角形的顶点.
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
新知探究
A
B
C
a
c
b
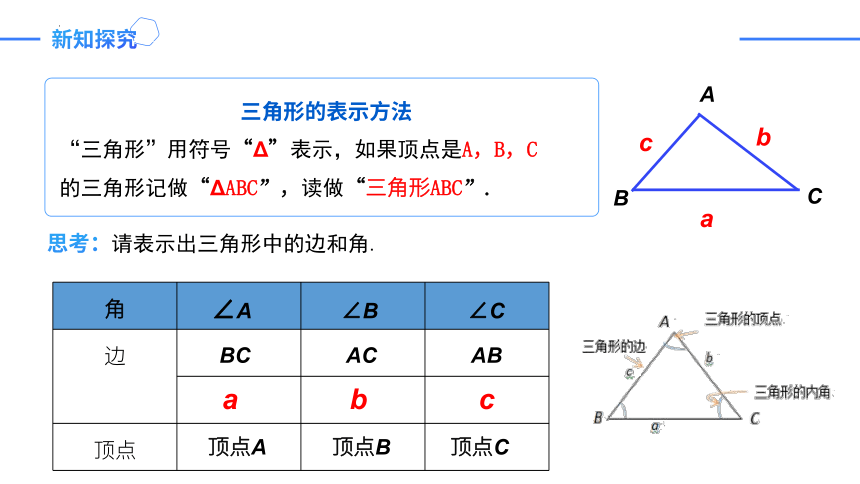
“三角形”用符号“Δ”表示,如果顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”.
三角形的表示方法
思考:请表示出三角形中的边和角.
角
边
顶点
BC AC AB
∠A ∠B ∠C
a b c
顶点A 顶点B 顶点C
新知探究
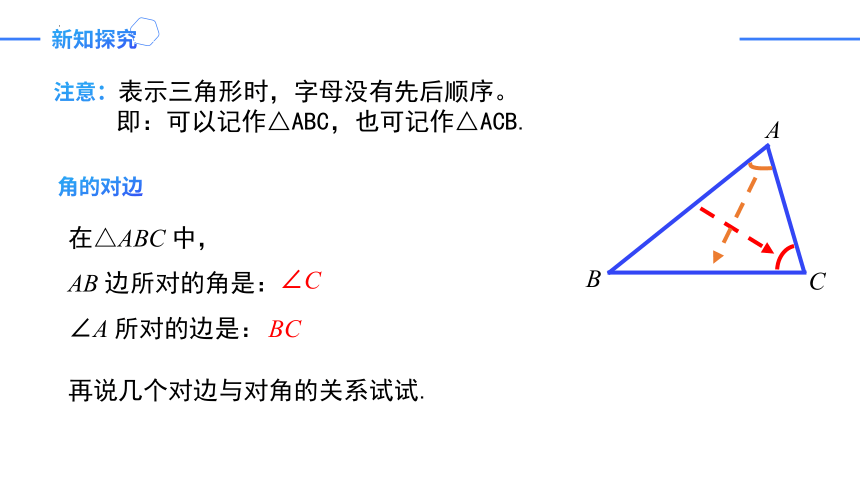
注意:表示三角形时,字母没有先后顺序。
即:可以记作△ABC,也可记作△ACB.
角的对边
在△ABC 中,
AB 边所对的角是:
∠A 所对的边是:
∠C
BC
再说几个对边与对角的关系试试.
B
C
A
典例精析
例2
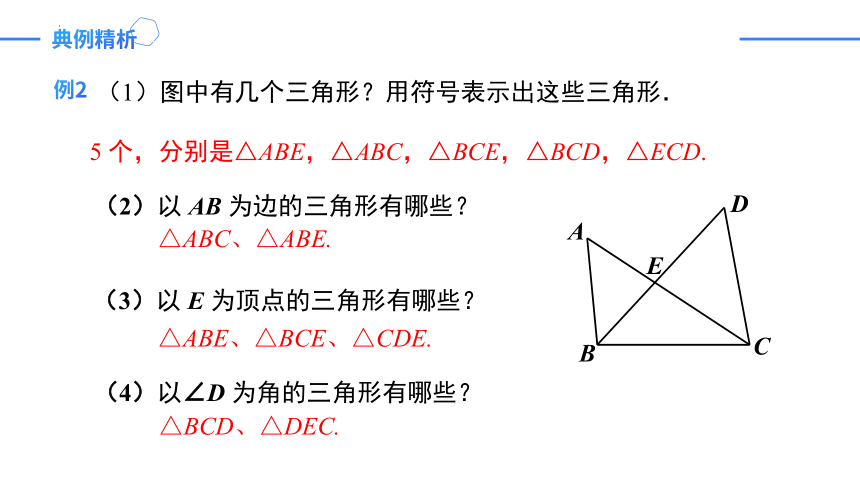
(1)图中有几个三角形?用符号表示出这些三角形.
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD.
(2)以 AB 为边的三角形有哪些?
△ABC、△ABE.
(3)以 E 为顶点的三角形有哪些?
△ABE、△BCE、△CDE.
(4)以∠D 为角的三角形有哪些?
△BCD、△DEC.
典例精析
例2
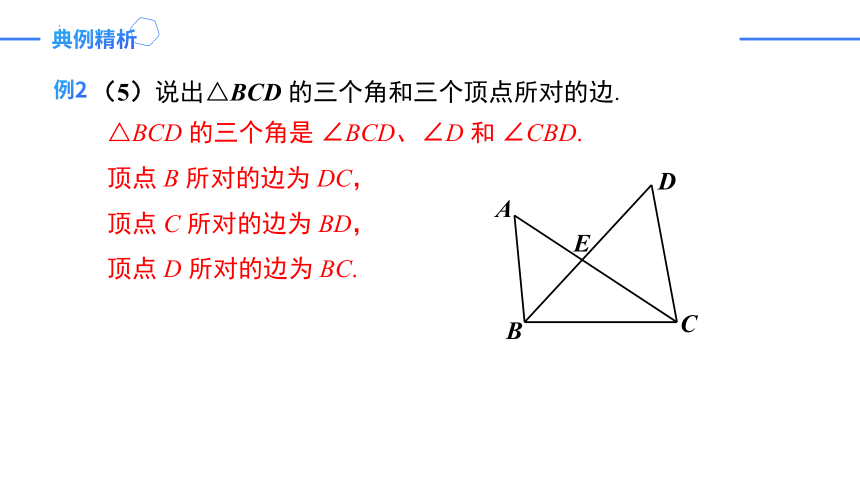
(5)说出△BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是 ∠BCD、∠D 和 ∠CBD.
A
B
C
D
E
顶点 B 所对的边为 DC,
顶点 C 所对的边为 BD,
顶点 D 所对的边为 BC.
新知探究
思考:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
钝角三角形
直角三角形
三角形
三角形的分类
直角三角形
锐角三角形
钝角三角形
新知探究
思考:你能找出下列三角形各自的特点吗?
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
三边均不相等
有两条边相等
三条边均相等
新知探究
思考:等边三角形和等腰三角形之间有什么关系?
归纳总结
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等腰三角形两边相等,等边三角形三边相等.
等边三角形是特殊的等腰三角形.
新知探究
思考:如何区分等腰三角形的元素?
腰
腰
底边
三角形
顶角
底角
底角
新知探究
思考:按照三角形三边情况,三角形可以分为哪几类?
三角形的分类
三角形
不等边三角形
等腰三角形
腰和底不等的三角形
等边三角形
典例精析
例3
判断以下命题的真假:
(2)等边三角形是特殊的等腰三角形. ( )
(1)一个钝角三角形一定不是等腰三角形. ( )
√
×
(3)等腰三角形的腰和底一定不相等. ( )
×
(4)等边三角形是锐角三角形. ( )
(5)直角三角形一定不是等腰三角形. ( )
×
√
(6)锐角三角形是三条边都不相等的三角形;( )
(7)等腰三角形是等边三角形; ( )
(8)等边三角形是等腰三角形. ( )
×
×
√
新知探究
思考:从A到C你会选择哪条路?
C
A
B
证明:
∵AB为线段
∴AC+BC>AB
(两点之间线段最短)
同理,AB+BC>AC
AC+AB>BC
新知探究
探究:任意选三根小棒,能围成一个三角形吗?先围一围,再与同学交流。
8cm
4cm
2cm
5cm
我围成了三角形。
我也围成了三角形。
为什么围不
成三角形呢?
为什么有的围的起来,有的围不起来呢?记录一下所有你围成的边长情况,分析交流一下吧!
新知探究
8cm
4cm
2cm
5cm
小棒长度 小棒长度 小棒长度 能否围成
第一次
第二次
第三次
第四次
8cm 4cm 5cm
能围成
4cm 5cm 2cm
能围成
8cm 4cm 2cm
不能围成
8cm 5cm 2cm
不能围成
任意选取三根小棒,围一围,发现有的能围成一个三角形,有的则不能。
新知探究
思考:以第三次为例,说明为什么不能构成三角形.
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形?
绿色和黄色的小棒太短了,
3根小棒不能首尾相接。
5厘米+ 2厘米< 8厘米,所以不能围成三角形。
新知探究
思考:根据以上结果,你能得出什么结论?
得出初步的结论:
两条短边的长度之和要大于最长的边。
探究:三角形任意两边长度的和真的是一定大于第三边吗?每位同学都来试试,先画一个三角形,再量一量、算一算,看看有没有能推翻这个结论的“例子”!
新知探究
探究:三角形任意两边长度的差又具有怎样的关系?量一量、算一算,看看能得到什么结论.
三角形的三边关系
三角形两边的和大于第三边.
三角形两边的差小于第三边.
即a+b>c,a+c>b,b+c>a
a-b归纳总结
典例精析
例4
下列长度的三条线段能否拼成三角形?为什么?
(1)3 cm、8 cm、4 cm;(2)5 cm、6 cm、11 cm;
(3)5 cm、6 cm、10 cm.
判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可.
解:(1)不能,因为 3 cm + 4 cm < 8 cm.
(2)不能,因为 5 cm + 6 cm = 11 cm.
(3)能,因为 5 cm + 6 cm > 10 cm.
典例精析
例5
若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
典例精析
例6
用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
解:(1)设底边长为x cm,则腰长为2x cm.
x + 2x + 2x =18.
解得 x =3.6.
所以,三边长分别为3.6 cm,7.2 cm,7.2 cm.
典例精析
例6
用一条长为18 cm的细绳围成一个等腰三角形.
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(2)①如果4 cm长的边为底边,设腰长为x cm,则
4 + 2x = 18. 解得 x = 7.
②如果4 cm长的边为腰,设底边长为x cm,则
4×2 + x = 18. 解得 x = 10.
因为4 + 4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长为4 的等腰三角形.
由以上讨论可知,第①种情况可以围成底边
长为4 cm的等腰三角形.
典例精析
例7
解:
∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
归纳总结
三角形的第三边长 x 满足两边之差<x<两边之和.
若三角形的三边长分别为a,b,
则第三边长度x应该满足:|a-b|当堂检测
1. 图中的锐角三角形有 ( )
A. 3 个 B. 4 个 C. 5 个 D. 6 个
A
2. 用木棒钉成一个三角架,两根小棒长分别是 7 cm 和 10 cm,
第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
3.如图,共有6个三角形,其中以AC为边的三角形是
________________________;
以∠B为内角的三角形有_________________________.
△ABC,△AEC,△ADC
△ABC,△DBC,△EBC
当堂检测
4.一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
5.下列长度的线段不能组成三角形的是( )
A. 3,8,4 B. 4,9,6
C. 15,20,8 D. 9,15,8
7 或8.5
A
6.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
当堂检测
7. 已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为 _______.
19 cm
8.若等腰三角形的两边长分别是3和4,则它的周长为 .
10或11
9.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
归纳总结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
应用
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
11.1.1
三角形的边
情景导入
猜谜:
形状似座山,
稳定性能坚.
三竿首尾连,
学问不简单.
情景导入
生活中的三角形
从古埃及的金字塔到现代大桥,都有什么样的形象?
在我们的生活中有没有这样的形象呢?试举例.
情景导入
生活中的三角形
新知探究
思考:观察三角形的形成过程,说一说什么叫三角形.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
三角形
要点
不在同一条直线上
要点1
三条线段
要点2
首尾顺次相接
要点3
典例精析
例1
下列图形是三角形吗?
不是
不是
是
不是
①位置关系:不在同一直线上;
②联接方式:首尾顺次相接.
三角形应满足以下两个条件:
新知探究
思考:观察如图所示的三角形,说一说三角形由哪些元素构成.
A
B
C
边
顶点
角
1
2
3
边:线段 AB,BC,CA 是三角形的边.
顶点:点 A,B,C 是三角形的顶点.
角:∠A,∠B,∠C 叫做三角形的内角,简称三角形的角.
新知探究
A
B
C
a
c
b
“三角形”用符号“Δ”表示,如果顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”.
三角形的表示方法
思考:请表示出三角形中的边和角.
角
边
顶点
BC AC AB
∠A ∠B ∠C
a b c
顶点A 顶点B 顶点C
新知探究
注意:表示三角形时,字母没有先后顺序。
即:可以记作△ABC,也可记作△ACB.
角的对边
在△ABC 中,
AB 边所对的角是:
∠A 所对的边是:
∠C
BC
再说几个对边与对角的关系试试.
B
C
A
典例精析
例2
(1)图中有几个三角形?用符号表示出这些三角形.
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD.
(2)以 AB 为边的三角形有哪些?
△ABC、△ABE.
(3)以 E 为顶点的三角形有哪些?
△ABE、△BCE、△CDE.
(4)以∠D 为角的三角形有哪些?
△BCD、△DEC.
典例精析
例2
(5)说出△BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是 ∠BCD、∠D 和 ∠CBD.
A
B
C
D
E
顶点 B 所对的边为 DC,
顶点 C 所对的边为 BD,
顶点 D 所对的边为 BC.
新知探究
思考:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
钝角三角形
直角三角形
三角形
三角形的分类
直角三角形
锐角三角形
钝角三角形
新知探究
思考:你能找出下列三角形各自的特点吗?
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
三边均不相等
有两条边相等
三条边均相等
新知探究
思考:等边三角形和等腰三角形之间有什么关系?
归纳总结
三条边各不相等的三角形叫作不等边三角形 ;
有两条边相等的三角形叫作等腰三角形;
三条边都相等的三角形叫作等边三角形.
等腰三角形两边相等,等边三角形三边相等.
等边三角形是特殊的等腰三角形.
新知探究
思考:如何区分等腰三角形的元素?
腰
腰
底边
三角形
顶角
底角
底角
新知探究
思考:按照三角形三边情况,三角形可以分为哪几类?
三角形的分类
三角形
不等边三角形
等腰三角形
腰和底不等的三角形
等边三角形
典例精析
例3
判断以下命题的真假:
(2)等边三角形是特殊的等腰三角形. ( )
(1)一个钝角三角形一定不是等腰三角形. ( )
√
×
(3)等腰三角形的腰和底一定不相等. ( )
×
(4)等边三角形是锐角三角形. ( )
(5)直角三角形一定不是等腰三角形. ( )
×
√
(6)锐角三角形是三条边都不相等的三角形;( )
(7)等腰三角形是等边三角形; ( )
(8)等边三角形是等腰三角形. ( )
×
×
√
新知探究
思考:从A到C你会选择哪条路?
C
A
B
证明:
∵AB为线段
∴AC+BC>AB
(两点之间线段最短)
同理,AB+BC>AC
AC+AB>BC
新知探究
探究:任意选三根小棒,能围成一个三角形吗?先围一围,再与同学交流。
8cm
4cm
2cm
5cm
我围成了三角形。
我也围成了三角形。
为什么围不
成三角形呢?
为什么有的围的起来,有的围不起来呢?记录一下所有你围成的边长情况,分析交流一下吧!
新知探究
8cm
4cm
2cm
5cm
小棒长度 小棒长度 小棒长度 能否围成
第一次
第二次
第三次
第四次
8cm 4cm 5cm
能围成
4cm 5cm 2cm
能围成
8cm 4cm 2cm
不能围成
8cm 5cm 2cm
不能围成
任意选取三根小棒,围一围,发现有的能围成一个三角形,有的则不能。
新知探究
思考:以第三次为例,说明为什么不能构成三角形.
长8厘米、5厘米和2厘米的三根小棒为什么不能围成三角形?
绿色和黄色的小棒太短了,
3根小棒不能首尾相接。
5厘米+ 2厘米< 8厘米,所以不能围成三角形。
新知探究
思考:根据以上结果,你能得出什么结论?
得出初步的结论:
两条短边的长度之和要大于最长的边。
探究:三角形任意两边长度的和真的是一定大于第三边吗?每位同学都来试试,先画一个三角形,再量一量、算一算,看看有没有能推翻这个结论的“例子”!
新知探究
探究:三角形任意两边长度的差又具有怎样的关系?量一量、算一算,看看能得到什么结论.
三角形的三边关系
三角形两边的和大于第三边.
三角形两边的差小于第三边.
即a+b>c,a+c>b,b+c>a
a-b
典例精析
例4
下列长度的三条线段能否拼成三角形?为什么?
(1)3 cm、8 cm、4 cm;(2)5 cm、6 cm、11 cm;
(3)5 cm、6 cm、10 cm.
判断三条线段是否可以组成三角形,只需判断两条较短线段长之和是否大于第三条线段长即可.
解:(1)不能,因为 3 cm + 4 cm < 8 cm.
(2)不能,因为 5 cm + 6 cm = 11 cm.
(3)能,因为 5 cm + 6 cm > 10 cm.
典例精析
例5
若三角形的两边长分别是2和7,第三边长为奇数,求第三边的长.
解:设第三边的长为x,
根据两边之和大于第三边得:
x<2+7即x<9
根据两边之差小于第三边得:
x>7-2即x>5
所以x的值大于5小于9,又因为它是奇数,
所以x只能取7。
典例精析
例6
用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
解:(1)设底边长为x cm,则腰长为2x cm.
x + 2x + 2x =18.
解得 x =3.6.
所以,三边长分别为3.6 cm,7.2 cm,7.2 cm.
典例精析
例6
用一条长为18 cm的细绳围成一个等腰三角形.
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(2)①如果4 cm长的边为底边,设腰长为x cm,则
4 + 2x = 18. 解得 x = 7.
②如果4 cm长的边为腰,设底边长为x cm,则
4×2 + x = 18. 解得 x = 10.
因为4 + 4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长为4 的等腰三角形.
由以上讨论可知,第①种情况可以围成底边
长为4 cm的等腰三角形.
典例精析
例7
解:
∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.
一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
归纳总结
三角形的第三边长 x 满足两边之差<x<两边之和.
若三角形的三边长分别为a,b,
则第三边长度x应该满足:|a-b|
1. 图中的锐角三角形有 ( )
A. 3 个 B. 4 个 C. 5 个 D. 6 个
A
2. 用木棒钉成一个三角架,两根小棒长分别是 7 cm 和 10 cm,
第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
3.如图,共有6个三角形,其中以AC为边的三角形是
________________________;
以∠B为内角的三角形有_________________________.
△ABC,△AEC,△ADC
△ABC,△DBC,△EBC
当堂检测
4.一个等腰三角形的周长为24cm,只知其中一边的长为7cm,则这个等腰三角形的腰长为_________cm.
5.下列长度的线段不能组成三角形的是( )
A. 3,8,4 B. 4,9,6
C. 15,20,8 D. 9,15,8
7 或8.5
A
6.下列说法:①等边三角形是等腰三角形;②三角形按边分类可分为等腰三角形、等边三角形、不等边三角形;③三角形的两边之差大于第三边;④三角形按角分类应分为锐角三角形、直角三角形、钝角三角形. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
当堂检测
7. 已知等腰三角形的两边长分别为 8 cm,3 cm,则这个三角形的周长为 _______.
19 cm
8.若等腰三角形的两边长分别是3和4,则它的周长为 .
10或11
9.若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
归纳总结
三角形
定义及其基本要素
顶点、角、边
分类
按角分类
按边分类
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
应用
