11.1 杠杆(提升篇)(有答案)2023-2024学年苏科版物理九年级上册
文档属性
| 名称 | 11.1 杠杆(提升篇)(有答案)2023-2024学年苏科版物理九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-07-02 17:14:24 | ||
图片预览




文档简介
2023年江苏省南京九年级物理上册课时练习
11.1 杠杆(提升篇)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,所使用的工具属于省力力杠杆的是( )
A. 羊角锤 B. 筷子
C. 天平 D. 镊子
2.如图所示,杠杆处于水平平衡状态。在杠杆两侧挂钩码处各减少一个质量相同的钩码,以下判断中正确的是( )
A.杠杆的左端下降 B.杠杆的右端下降
C.杠杆仍然保持水平平衡 D.以上情况都有可能发生
3.如图所示是用长棒撬石块的示意图,当在A点用竖直向下的力F1压长棒时,石块未撬动。采取下列措施,最有利于把石块撬动的一项是( )
A.把垫着的小石块移得离大石块近一点,而且用力方向改为F2方向
B.把垫着的小石块移得离大石块近一点,而且用力方向仍为F1方向
C.把垫着的小石块移得离大石块远一点,而且用力方向改为F2方向
D.把垫着的小石块移得离大石块远一点,而且用力方向仍为F1方向
4.下列关于杠杆的说法中,正确的是( )
A.杠杆一定有支点,但支点不一定在杠杆上
B.省力杠杆可以省力,有时也能省距离
C.杠杆的长度等于动力臂与阻力臂之和
D.杠杆的力臂可以不在杠杆上
5.筷子是我们日常生活中普遍使用的餐具,如图所示将AB这支筷子作为杠杆,O点为支点,食指指头对筷子上M点的压力(垂直于筷子)是动力。则( )
A.阻力臂是MN、动力臂是OM
B.阻力是筷子对食物的压力
C.阻力的方向向上
D.把食物靠近支点放置时,食指对筷子上M点的压力变大
6.如图甲所示,长的粗细均匀的光滑金属杆可绕点转动,杆上有一光滑滑环,用竖直向上的测力计拉着滑环缓慢向右移动,使杆保持水平状态,测力计示数与滑环离开点的距离的关系如图乙所示,则下列说法正确的是( )
A.滑环的重力为 B.滑环的重力为
C.杠杆的重力为 D.杠杆的重力为
7.《墨经》最早记述了杆秤的杠杆原理,如图所示。把物品挂在挂钩上,将秤砣拨到合适位置,待秤杆平衡后,根据秤砣绳所对应的刻度就可得出物品的质量。下列有关说法正确的是( )
A.增大物重时,应把“權”向左端移 B.增大物重时,应把“權”向右端移
C.“權”小于物重时,右端一定上扬 D.若“權”发生磨损,则测得的物重偏小
8.如图所示,作用在铁棒的一端、且始终与铁棒垂直的力F,将铁棒绕着O点,逆时针缓慢转动30°角至水平位置。在此过程中,F的大小与铁棒重力的力臂l的关系图像可能是( )
A. B. C. D.
二、填空题
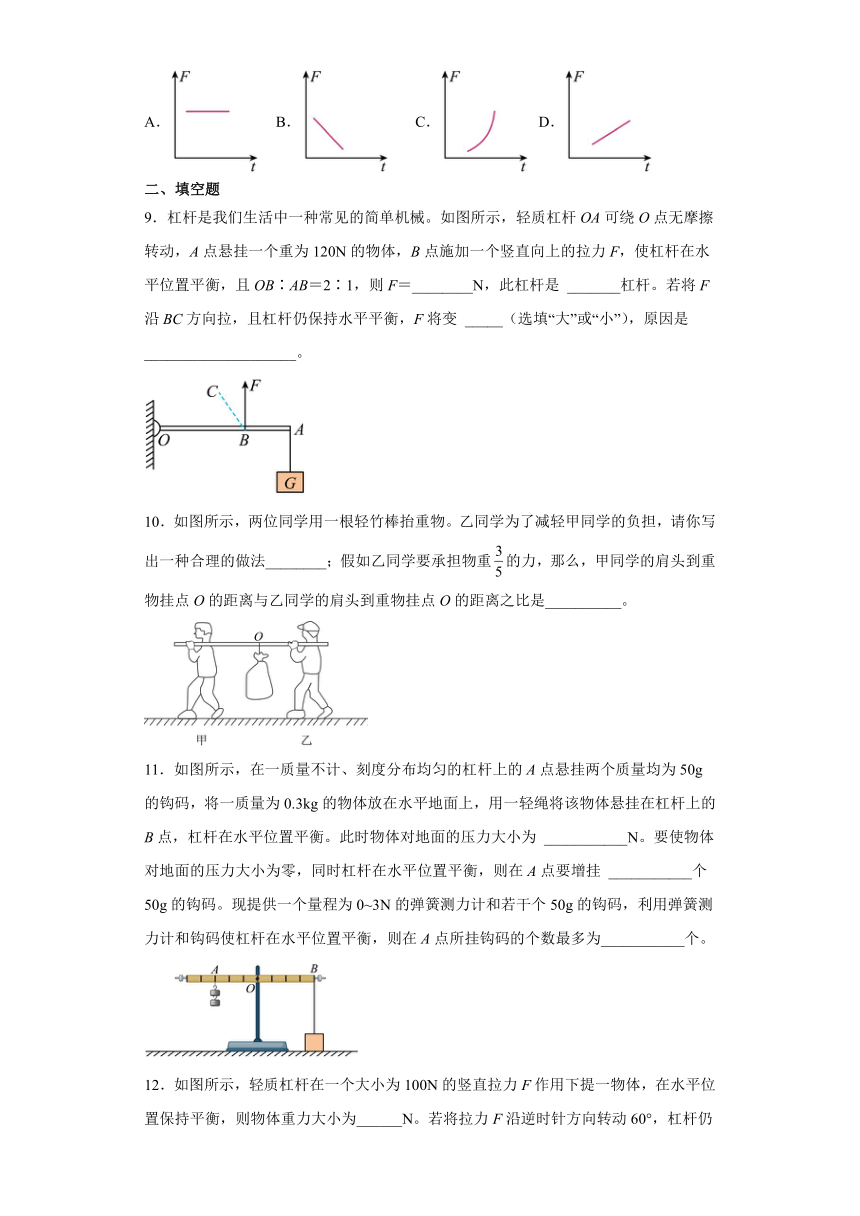
9.杠杆是我们生活中一种常见的简单机械。如图所示,轻质杠杆OA可绕O点无摩擦转动,A点悬挂一个重为120N的物体,B点施加一个竖直向上的拉力F,使杠杆在水平位置平衡,且OB∶AB=2∶1,则F=________N,此杠杆是 _______杠杆。若将F沿BC方向拉,且杠杆仍保持水平平衡,F将变 _____(选填“大”或“小”),原因是 ____________________。
10.如图所示,两位同学用一根轻竹棒抬重物。乙同学为了减轻甲同学的负担,请你写出一种合理的做法________;假如乙同学要承担物重的力,那么,甲同学的肩头到重物挂点O的距离与乙同学的肩头到重物挂点O的距离之比是__________。
11.如图所示,在一质量不计、刻度分布均匀的杠杆上的A点悬挂两个质量均为50g的钩码,将一质量为0.3kg的物体放在水平地面上,用一轻绳将该物体悬挂在杠杆上的B点,杠杆在水平位置平衡。此时物体对地面的压力大小为 ___________N。要使物体对地面的压力大小为零,同时杠杆在水平位置平衡,则在A点要增挂 ___________个50g的钩码。现提供一个量程为0~3N的弹簧测力计和若干个50g的钩码,利用弹簧测力计和钩码使杠杆在水平位置平衡,则在A点所挂钩码的个数最多为___________个。
12.如图所示,轻质杠杆在一个大小为100N的竖直拉力F作用下提一物体,在水平位置保持平衡,则物体重力大小为______N。若将拉力F沿逆时针方向转动60°,杠杆仍在水平位置平衡,拉力大小将______(选填“增大”“减小”或“不变”)。
13.如图所示,在一质量不计、刻度分布均匀的杠杆上的A点悬挂两个质量均为50g的钩码,将一质量为0.3kg、底面积为100cm2的物体放在水平地面上,用一轻绳将该物体悬挂在杠杆上的B点,杠杆在水平位置平衡。此时轻绳对杠杆的拉力大小为 ___________N,物体对地面的压力大小为 ___________N,物体对地面的压强为 ___________Pa。(g=10N/kg)
14.如图,一根形状不规则的木棒水平放置于地面上,采用如下方法测定其重量:在木棒左端以F1=4N的竖直向上的力刚好能提起木棒,在木棒右端以F2=6N的竖直向上的力也能刚好提起木棒。这根木棒的重力为___________。木棒平放在地面上远比竖起来要稳定,这是因为木棒的___________ 越低越稳定。
15.长为80cm的直杠杆,支点离右端20cm,左端挂20N的重物,在右端应挂___________ N的重物杠杆才能平衡,如果两端各加10N的重物,则杠杆___________ 端向上抬起,若要杠杆恢复平衡,支点应向___________移动。
16.实践创新小组的成员小明对家中使用的杆秤(该杆秤有两个提纽)很感兴趣,并选择了提纽1来测量物体质量,如图所示,已知秤砣重力为2N,提纽1到秤盘的水平距离为5cm,当秤砣距提纽1的水平距离为15cm时,杆秤恰好平衡,不计秤杆、秤盘及细绳的质量,则物体质量为___________kg,若小明用提纽2来测量该物体,秤砣应向___________(选填“左”或“右”)移动。
三、作图题
17.如图所示,生活中的剪刀可看作杠杆,O为支点,要用剪刀将竹签剪断,画出图中动力F1的力臂l1,并在A点画出阻力F2的示意图。
18.图甲是用钳子剪物体的情景,图乙是其简化图,M点是杠杆动力的作用点,O点是支点,F2是杠杆受到的阻力,请画出最小动力F1的示意图及其力臂l1。
四、实验题
19.如图所示是小红和小华同学探究“杠杆平衡的条件”的几个实验情景:
(1)挂钩码前,杠杆在如图甲所示的位置静止,此时杠杆___________(选填“达到”或“没有达到”)平衡状态;若要使杠杆在水平位置平衡,应将右端的平衡螺母向___________调。调节杠杆在水平位置平衡,除了可以消除杠杆重力对实验的影响,在实验测量时还有一个优点,请你写出:___________________。
(2)杠杆调节好后,小红进行了两次实验,实验如图乙、丙所示。她测量出两边钩码的重力分别为动力和阻力,对应的作用点到支点的距离为和,并将数据记录在下表。
动力/N 阻力/N 支点到动力作用点的距离/m 支点到阻力作用点的距离/m
1 0.5 0.15 0.3
1.5 1 0.2 0.3
记录数据后,同桌的小华根据数据得出杠杆平衡条件:___________(字母公式)。为了进一步完善实验,应该进行多次实验,目的是:___________(选填“减小误差”或“得到普遍规律”);
(3)如图,若不在B点挂钩码,可改用弹簧测力计在B点向下拉杠杆,当测力计从a位置转动到b位置时,使杠杆仍在水平位置平衡,其示数大小将_______(选填“变大”或“变小”)
五、计算题
20.水平桌面上有一个底面积为200cm2的圆柱形容器,容器中水的深度为15cm。如图所示,用细线将一质量忽略不计的杠杆悬挂起来,把质量为0.3kg的物体A用细线悬挂在杠杆C处,再把体积为400cm3的物体B(不吸水)用细线悬挂在杠杆D处,当物体B浸没在水中静止时,杠杆恰好在水平位置平衡,此时C、D两点到支点O的距离分别为10cm、15cm。求:
(1)物体B受到的浮力;
(2)物体B浸没在水中静止时,水对容器底部的压强;
(3)细线对物体B的拉力及物体B的密度。
21.为了进一步丰富群众文化生活,某公园全新打造的水上舞台成了又一靓丽景观。其舞台简化图如图甲所示,舞台架两侧的底部安装有若干体积为1.5m3的水箱,空水箱的质量为450kg,舞台上的传感器设备可以控制往水箱中充水或从水箱向外排水,从而保持水箱的上表面与水面始终相平,实现真正的半自动化控制。已知该舞台和舞台架(不含水箱)的总质量为10t,粗略认为其重心在图中O点,该舞台可以允许承受的演员和设备的总质量最大为6t。
(1)舞台的上表面有一层专用的舞台地板,它的材料中含有一定量的聚氯乙烯,具有不涩、不滑、柔韧性好的特征,有一定的缓冲作用。已知其中一块地板长度为50cm,宽度为30cm,厚度为4cm,质量为10.8kg,则该地板的密度是多少?
(2)当舞台以允许承载的最大载荷进行表演时,为了安全,每个水箱中至少还得保留50kg的水以防意外,若按照此要求设计舞台,至少需要安装几个水箱?
(3)如果舞台上质量分布不均匀,容易导致舞台侧翻,传感器设备可以通过控制左、右两侧水箱中的水量来避免危险的发生。如图乙所示,某次演出时将质量为2t的设备C放在舞台上,其重心距离O点的水平距离为20m,两侧水箱重心A、B到O点的水平距离为25m,此时通过传感器控制左、右两侧水箱中水的总体积分别为V1、V2,则V1和V2的差为多少立方米?
试卷第1页,共3页
参考答案:
1.A
【详解】A.羊角锤在使用时,动力臂大于阻力臂,属于省力杠杆,故A符合题意;
BD.筷子和镊子使用时,阻力臂大于动力臂,属于费力杠杆,故BD不符合题意;
C.天平使用时,动力臂等于阻力臂,属于等臂杠杆,故C不符合题意。
故选A。
2.B
【详解】令一个钩码的重力为G,杠杆上一格的刻度长为L,当杠杆两侧挂钩码处各减少一个质量相同的钩码后,左边的力臂与力的乘积F1L1=G×3L=3GL
右边的力臂与力的乘积F1L1=2G×2L=4GL
因为F1L1故选B。
3.A
【详解】把垫着的小石块移得离大石块近一点,此时阻力臂变短,根据力臂定义可知,用力方向改为F2方向时,动力臂最长,根据杠杆平衡条件可知,动力臂越长、阻力臂越短,越省力,越有利于撬动石块。故A符合题意,BCD不符合题意。
故选A。
4.D
【详解】A.杠杆是一根能绕固定点转动的硬棒,这个固定点是杠杆的支点,支点一定在杠杆上,支点可以在杠杆的任意位置,故A错误;
B.省力杠杆可以省力,一定费距离,既省力又省距离的杠杆是不存在的,故B错误;
C.杠杆的长度和动力臂、阻力没有必然的联系,故C错误;
D.力臂是支点到力的作用线的距离,力臂可以在杠杆上,也可以不在杠杆上,故D正确。
故选D。
5.C
【详解】ABC.由图可知,杠杆绕O点转动,O点为支点,作用在M点向下的是动力,是手对筷子的力,作用在N点向上的力阻碍杠杆转动是阻力,阻力是食物对筷子的压力,分别从支点O向阻力作用线、动力作用线作垂线,就得到阻力臂ON,动力臂OM,故AB不符合题意,C符合题意;
D.把食物靠近支点放置时,阻力臂变小,阻力不变,阻力臂和阻力的乘积变小,动力臂不变,由杠杆平衡条件可知,动力变小,所以食指对筷子上M点的压力变小,故D不符合题意。
故选C。
6.A
【详解】由图甲可知,金属杆是粗细均匀的一只杠杆,绕点转动,金属杆的重心在杠杆的中点,阻力阻力臂为
用竖直向上的测力计拉着滑环缓慢向右移动时,滑环对金属杆的拉力等于测力计的拉力与滑环的重力之差,由图乙可知,当时,动力
则根据杠杆平衡的条件可得即┄┄①
当时,动力
则根据杠杆平衡的条件可得即┄┄②
解可得,
故A正确,BCD错误。
故选。
7.B
【详解】AB.增大物重时,阻力变大,由于动力和阻力臂不变,根据杠杆平衡条件:动力动力臂阻力阻力臂可知,应把动力臂变大,即把“權”向右端移,故A错误,B正确;
C.“權”小于物重时,动力小于阻力,根据杠杆平衡条件可知:当动力臂大于阻力臂时,杠杆可能在水平位置平衡,所以右端不一定上扬,故C错误;
D.若“權”发生磨损,动力变小,阻力不变,阻力臂不变,根据杠杆平衡条件可得,动力臂变大,即测量值比真实值偏大,故D错误。
故选B。
8.D
【详解】根据杠杆平衡原理可得
逆时针缓慢 转动30°角至水平位置动力臂l1不变,但是阻力臂l在不断的增大,故
成正比关系,故D符合题意,ABC不符合题意。
故选D。
9. 180 费力 大 见解析
【详解】[1][2]OB∶AB=2∶1,则OB∶OA=2∶3;杠杆水平平衡时,A端受到的阻力大小
FA=G物=120N,动力F的力臂为OB,阻力FA的力臂为OA,由杠杆平衡条件F1l1=F2l2可得F×OB=FA×OA
因为OB<OA,所以F>FA,即杠杆为费力杠杆。动力的大小为
[3][4]若其他条件不变,将F沿BC方向拉杠杆仍在水平位置平衡,拉力的力臂减小,阻力和阻力臂不变,根据杠杆的平衡条件F1l1=F2l2可知,拉力将变大。
10. 将重物远离甲同学 3:2
【详解】[1]由杠杆平衡条件得,要减轻甲同学的负担,即省力,要增大甲同学到支点O的距离,即增大动力臂,故要将重物远离甲同学。
[2]由得
11. 2.25 6 10
【详解】[1]两个质量均为50g的钩码的重力为:G=mg=0.1kg×10N/kg=1N
设杠杆上每个小格的长度为L;杠杆在水平位置平衡,根据杠杆的平衡条件可知FBLB=GLA
即FB×4L=1N×3L,解得F1=0.75N。物体的重力为G'=m'g=0.3kg×10N/kg=3N
物体受到竖直向下的重力、竖直向上的支持力和拉力的作用,根据平衡力和相互作用力可知地面对物体的支持力的大小为F支=G'-F1=3N-0.75N=2.25N
[2]要使物体对地面的压力大小为零,同时杠杆在水平位置平衡,此时物体对杠杆的拉力为3N;根据杠杆的平衡条件可知3N×4L=G"×3L
解得G"=4N;每个钩码的重力为0.5N;则A端所挂钩码的个数为
则加挂的钩码的个数Δn=8-2=6
[3]要使在A点所挂钩码的个数最多,钩码对杠杆的拉力的力臂不变,当弹簧测力计示数最大即弹簧测力计对杠杆拉力的力臂最大时,所挂钩码个数最大;弹簧测力计的最大称量值为3N,最大力臂为5L,根据杠杆的平衡条件可知3N×5L=GA×3L
解得GA=5N;每个钩码的重力为0.5N,则A点所挂钩码的最多个数为
12. 400 增大
【详解】[1]如图,杠杆的动力臂为4l,阻力臂为l,根据杠杆平衡条件可得,物体的重为
[2]若将拉力F沿逆时针方向转动60°,杠杆仍在水平位置平衡,此时阻力和阻力臂不变,动力臂变短,根据杠杆平衡条件可知,拉力将增大。
13. 0.75 2.25 225
【详解】[1]两个质量均为50g的钩码的质量为m=50g×2=100g=0.1kg
则两个钩码的重力为G=mg=0.1kg×10N/kg=1N
设杠杆上每个小格的长度为L;杠杆在水平位置平衡,由于杠杆的平衡条件F1L1=G1L2知道,即F1×4L=1N×3L解得F1=0.75N
[2]物体的重力为G'=m'g=0.3kg×10N/kg=3N
物体受到竖直向下的重力、竖直向上的支持力和拉力的作用,则地面对物体的支持力的大小为F支=G'﹣F1=3N﹣0.75N=2.25N
根据力的相互作用可知物体对地面压力的大小为F压=F支=2.25N
[3]物体对地面的压强
14. 10N 重心
【详解】[1]假设木棒的重心到B点的距离为OB,到A点的距离为OA,当在木棒左端以F1=4N的竖直向上的力刚好能提起木棒时,支点在A点,根据杠杆平衡的条件,则有
F1×AB=G×OA,当在木棒右端以F2=6N的竖直向上的力也能刚好提起木棒,支点在B点,根据杠杆平衡的条件,则有G×OB= F2×AB因为OA+OB=AB
这根木棒的重力为G=F1+F2=4N+6N=10N
[2]提高物体稳度有两种方法,分别是:增大支撑面积和降低重心。木棒平放在地面上远比竖起来要稳定,这是通过降低重心的方增大物体的稳定程度的。
15. 60 右 左
【详解】[1]由题意知,长为80cm的直杠杆,支点离右端20cm,支点离左端为80cm-20cm=60cm,杠杆左端的力臂长度l1=60cm,杠杆右端力臂的长度l2=20cm,根据杠杆平衡的条件,F1l1=F2l2可知,杠杆右端重物的重力为
[2]两端各加10N的重物后,杠杆左端G左l1=(20N+10N)×60cm=30N×60cm
杠杆右端G右l2=(60N+10N)×20cm=70N×20cm
由于G左l1>G右l2,杠杆的右端向上抬起。
[3]因为G左l1>G右l2,G左和G右是定值,只能减小l1,增大l2,将杠杆的支点向左移动。
16. 0.6 右
【详解】[1]由图中可知,该装置构成一个杠杆,支点为提扭1,动力F1等于秤砣重力,即F1=2N,秤砣与提纽1的水平距离为动力臂l1,即l1=15cm=0.15m
提纽1到秤盘的水平距离为阻力臂l2,即l2=5cm=0.05m
杆秤平衡时,由杠杆的平衡条件可得F1l1=F2l2
解得阻力为
物体的重力G物等于阻力F2,即G物=F2=6N
由G=mg可得,物体的质量为
[2]若小明用提纽2来测量该物体,可知阻力臂减小,而阻力不变,且动力也不变,故由杠杆的平衡条件可知,要使杆秤平衡,则动力臂应减小,即秤砣应向右移动。
17.
【详解】过支点做动力F1的垂线,则垂线段为力臂l1;连接OA,即为阻力臂,阻力F2垂直于阻力臂OA,由于阻力阻碍剪刀口闭合,所以力的方向向下,如下图所示:
18.
【详解】已知动力的作用点为M,则OM就是最长的动力臂,在阻力、阻力臂一定时,由杠杆平衡的条件F1l1=F2l2可知,此时动力最小,且方向垂直与力臂向下,据此画出最小的动力,如图所示:
19. 达到 右 直接在杠杆上读出力臂的大小 F1l1=F2l2 得到普遍规律 变大
【详解】(1)[1]挂钩码前,杠杆在如图甲所示的位置静止,因为杠杆处于静止状态,所以此时杠杆达到平衡状态。
[2]杠杆在如图甲所示的位置静止,左侧下沉,说明此时重心偏左,若要使杠杆在水平位置平衡,应将右端的平衡螺母向右调。
[3]调节杠杆在水平位置平衡,除了可以消除杠杆重力对实验的影响,在实验测量时还可以直接在杠杆上读出力臂的大小。
(2)[4]记录数据后,根据数据得出杠杆平衡条件F1l1=F2l2。
[5]进行多次实验,目的是得到普遍规律。
(3)[6]当测力计从a位置转动到b位置时,力臂变小,根据杠杆平衡条件可知,其示数大小将变大。
20.(1)4N;(2);(3)
【详解】解:(1)因为物体B浸没在水中
物体B受到的浮力
(2)物体B浸没在水中后液面上升的高度
物体B浸没在水中时容器中水深
物体B浸没在水中静止时,水对容器的压强
(3)物体A的重力
细线对杠杆的拉力为和
根据杠杆的平衡条件得
细线对B的拉力为
对物体B受力分析得
由得,物体B的质量
物体B的密度
答:(1)物体B受到的浮力4N;
(2)物体B浸没在水中静止时,水对容器底部的压强;
(3)细线对物体B的拉力及物体B的密度。
21.(1)1.8×103kg/m3;(2)16个水箱;(3)1.6m3
【详解】解:(1)该地板的底面积
地板的体积
地板的质量m=10.8kg,则地板的密度为
(2)设需要安装n个水箱;已知空水箱的质量为m0=450kg,每个水箱中水的质量m水=50kg,舞台和舞台架(不含水箱)的总质量为m台=10t=1×104kg,该舞台可以允许承受的演员和设备的总质量最大为m大=6t=6×103kg,则总质量为
总重力为
已知水箱的体积为1.5m3,当水箱的上表面与水面始终相平时,根据阿基米德原理可知,n个水箱悬浮时受到的浮力为
由于舞台漂浮在水面上,故F浮=G总,即
解得:n=16。
(3)A、B两端水箱提供的浮力大小均为
A、B两端水箱中水的重力为GA和GB,故A端水箱给舞台提供的支持力为
同理,B端水箱给舞台提供的支持力为
A的力臂为l1=25m,B的力臂l2=25m;C的重力
C的力臂为l3=20m;根据杠杆平衡条件可知,
即
解得
化简为
再次化简为
答:(1)该地板的密度是1.8×103kg/m3;
(2)若按照此要求设计舞台,至少需要安装16个水箱;
(3)V1和V2的差为1.6m3
11.1 杠杆(提升篇)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,所使用的工具属于省力力杠杆的是( )
A. 羊角锤 B. 筷子
C. 天平 D. 镊子
2.如图所示,杠杆处于水平平衡状态。在杠杆两侧挂钩码处各减少一个质量相同的钩码,以下判断中正确的是( )
A.杠杆的左端下降 B.杠杆的右端下降
C.杠杆仍然保持水平平衡 D.以上情况都有可能发生
3.如图所示是用长棒撬石块的示意图,当在A点用竖直向下的力F1压长棒时,石块未撬动。采取下列措施,最有利于把石块撬动的一项是( )
A.把垫着的小石块移得离大石块近一点,而且用力方向改为F2方向
B.把垫着的小石块移得离大石块近一点,而且用力方向仍为F1方向
C.把垫着的小石块移得离大石块远一点,而且用力方向改为F2方向
D.把垫着的小石块移得离大石块远一点,而且用力方向仍为F1方向
4.下列关于杠杆的说法中,正确的是( )
A.杠杆一定有支点,但支点不一定在杠杆上
B.省力杠杆可以省力,有时也能省距离
C.杠杆的长度等于动力臂与阻力臂之和
D.杠杆的力臂可以不在杠杆上
5.筷子是我们日常生活中普遍使用的餐具,如图所示将AB这支筷子作为杠杆,O点为支点,食指指头对筷子上M点的压力(垂直于筷子)是动力。则( )
A.阻力臂是MN、动力臂是OM
B.阻力是筷子对食物的压力
C.阻力的方向向上
D.把食物靠近支点放置时,食指对筷子上M点的压力变大
6.如图甲所示,长的粗细均匀的光滑金属杆可绕点转动,杆上有一光滑滑环,用竖直向上的测力计拉着滑环缓慢向右移动,使杆保持水平状态,测力计示数与滑环离开点的距离的关系如图乙所示,则下列说法正确的是( )
A.滑环的重力为 B.滑环的重力为
C.杠杆的重力为 D.杠杆的重力为
7.《墨经》最早记述了杆秤的杠杆原理,如图所示。把物品挂在挂钩上,将秤砣拨到合适位置,待秤杆平衡后,根据秤砣绳所对应的刻度就可得出物品的质量。下列有关说法正确的是( )
A.增大物重时,应把“權”向左端移 B.增大物重时,应把“權”向右端移
C.“權”小于物重时,右端一定上扬 D.若“權”发生磨损,则测得的物重偏小
8.如图所示,作用在铁棒的一端、且始终与铁棒垂直的力F,将铁棒绕着O点,逆时针缓慢转动30°角至水平位置。在此过程中,F的大小与铁棒重力的力臂l的关系图像可能是( )
A. B. C. D.
二、填空题
9.杠杆是我们生活中一种常见的简单机械。如图所示,轻质杠杆OA可绕O点无摩擦转动,A点悬挂一个重为120N的物体,B点施加一个竖直向上的拉力F,使杠杆在水平位置平衡,且OB∶AB=2∶1,则F=________N,此杠杆是 _______杠杆。若将F沿BC方向拉,且杠杆仍保持水平平衡,F将变 _____(选填“大”或“小”),原因是 ____________________。
10.如图所示,两位同学用一根轻竹棒抬重物。乙同学为了减轻甲同学的负担,请你写出一种合理的做法________;假如乙同学要承担物重的力,那么,甲同学的肩头到重物挂点O的距离与乙同学的肩头到重物挂点O的距离之比是__________。
11.如图所示,在一质量不计、刻度分布均匀的杠杆上的A点悬挂两个质量均为50g的钩码,将一质量为0.3kg的物体放在水平地面上,用一轻绳将该物体悬挂在杠杆上的B点,杠杆在水平位置平衡。此时物体对地面的压力大小为 ___________N。要使物体对地面的压力大小为零,同时杠杆在水平位置平衡,则在A点要增挂 ___________个50g的钩码。现提供一个量程为0~3N的弹簧测力计和若干个50g的钩码,利用弹簧测力计和钩码使杠杆在水平位置平衡,则在A点所挂钩码的个数最多为___________个。
12.如图所示,轻质杠杆在一个大小为100N的竖直拉力F作用下提一物体,在水平位置保持平衡,则物体重力大小为______N。若将拉力F沿逆时针方向转动60°,杠杆仍在水平位置平衡,拉力大小将______(选填“增大”“减小”或“不变”)。
13.如图所示,在一质量不计、刻度分布均匀的杠杆上的A点悬挂两个质量均为50g的钩码,将一质量为0.3kg、底面积为100cm2的物体放在水平地面上,用一轻绳将该物体悬挂在杠杆上的B点,杠杆在水平位置平衡。此时轻绳对杠杆的拉力大小为 ___________N,物体对地面的压力大小为 ___________N,物体对地面的压强为 ___________Pa。(g=10N/kg)
14.如图,一根形状不规则的木棒水平放置于地面上,采用如下方法测定其重量:在木棒左端以F1=4N的竖直向上的力刚好能提起木棒,在木棒右端以F2=6N的竖直向上的力也能刚好提起木棒。这根木棒的重力为___________。木棒平放在地面上远比竖起来要稳定,这是因为木棒的___________ 越低越稳定。
15.长为80cm的直杠杆,支点离右端20cm,左端挂20N的重物,在右端应挂___________ N的重物杠杆才能平衡,如果两端各加10N的重物,则杠杆___________ 端向上抬起,若要杠杆恢复平衡,支点应向___________移动。
16.实践创新小组的成员小明对家中使用的杆秤(该杆秤有两个提纽)很感兴趣,并选择了提纽1来测量物体质量,如图所示,已知秤砣重力为2N,提纽1到秤盘的水平距离为5cm,当秤砣距提纽1的水平距离为15cm时,杆秤恰好平衡,不计秤杆、秤盘及细绳的质量,则物体质量为___________kg,若小明用提纽2来测量该物体,秤砣应向___________(选填“左”或“右”)移动。
三、作图题
17.如图所示,生活中的剪刀可看作杠杆,O为支点,要用剪刀将竹签剪断,画出图中动力F1的力臂l1,并在A点画出阻力F2的示意图。
18.图甲是用钳子剪物体的情景,图乙是其简化图,M点是杠杆动力的作用点,O点是支点,F2是杠杆受到的阻力,请画出最小动力F1的示意图及其力臂l1。
四、实验题
19.如图所示是小红和小华同学探究“杠杆平衡的条件”的几个实验情景:
(1)挂钩码前,杠杆在如图甲所示的位置静止,此时杠杆___________(选填“达到”或“没有达到”)平衡状态;若要使杠杆在水平位置平衡,应将右端的平衡螺母向___________调。调节杠杆在水平位置平衡,除了可以消除杠杆重力对实验的影响,在实验测量时还有一个优点,请你写出:___________________。
(2)杠杆调节好后,小红进行了两次实验,实验如图乙、丙所示。她测量出两边钩码的重力分别为动力和阻力,对应的作用点到支点的距离为和,并将数据记录在下表。
动力/N 阻力/N 支点到动力作用点的距离/m 支点到阻力作用点的距离/m
1 0.5 0.15 0.3
1.5 1 0.2 0.3
记录数据后,同桌的小华根据数据得出杠杆平衡条件:___________(字母公式)。为了进一步完善实验,应该进行多次实验,目的是:___________(选填“减小误差”或“得到普遍规律”);
(3)如图,若不在B点挂钩码,可改用弹簧测力计在B点向下拉杠杆,当测力计从a位置转动到b位置时,使杠杆仍在水平位置平衡,其示数大小将_______(选填“变大”或“变小”)
五、计算题
20.水平桌面上有一个底面积为200cm2的圆柱形容器,容器中水的深度为15cm。如图所示,用细线将一质量忽略不计的杠杆悬挂起来,把质量为0.3kg的物体A用细线悬挂在杠杆C处,再把体积为400cm3的物体B(不吸水)用细线悬挂在杠杆D处,当物体B浸没在水中静止时,杠杆恰好在水平位置平衡,此时C、D两点到支点O的距离分别为10cm、15cm。求:
(1)物体B受到的浮力;
(2)物体B浸没在水中静止时,水对容器底部的压强;
(3)细线对物体B的拉力及物体B的密度。
21.为了进一步丰富群众文化生活,某公园全新打造的水上舞台成了又一靓丽景观。其舞台简化图如图甲所示,舞台架两侧的底部安装有若干体积为1.5m3的水箱,空水箱的质量为450kg,舞台上的传感器设备可以控制往水箱中充水或从水箱向外排水,从而保持水箱的上表面与水面始终相平,实现真正的半自动化控制。已知该舞台和舞台架(不含水箱)的总质量为10t,粗略认为其重心在图中O点,该舞台可以允许承受的演员和设备的总质量最大为6t。
(1)舞台的上表面有一层专用的舞台地板,它的材料中含有一定量的聚氯乙烯,具有不涩、不滑、柔韧性好的特征,有一定的缓冲作用。已知其中一块地板长度为50cm,宽度为30cm,厚度为4cm,质量为10.8kg,则该地板的密度是多少?
(2)当舞台以允许承载的最大载荷进行表演时,为了安全,每个水箱中至少还得保留50kg的水以防意外,若按照此要求设计舞台,至少需要安装几个水箱?
(3)如果舞台上质量分布不均匀,容易导致舞台侧翻,传感器设备可以通过控制左、右两侧水箱中的水量来避免危险的发生。如图乙所示,某次演出时将质量为2t的设备C放在舞台上,其重心距离O点的水平距离为20m,两侧水箱重心A、B到O点的水平距离为25m,此时通过传感器控制左、右两侧水箱中水的总体积分别为V1、V2,则V1和V2的差为多少立方米?
试卷第1页,共3页
参考答案:
1.A
【详解】A.羊角锤在使用时,动力臂大于阻力臂,属于省力杠杆,故A符合题意;
BD.筷子和镊子使用时,阻力臂大于动力臂,属于费力杠杆,故BD不符合题意;
C.天平使用时,动力臂等于阻力臂,属于等臂杠杆,故C不符合题意。
故选A。
2.B
【详解】令一个钩码的重力为G,杠杆上一格的刻度长为L,当杠杆两侧挂钩码处各减少一个质量相同的钩码后,左边的力臂与力的乘积F1L1=G×3L=3GL
右边的力臂与力的乘积F1L1=2G×2L=4GL
因为F1L1
3.A
【详解】把垫着的小石块移得离大石块近一点,此时阻力臂变短,根据力臂定义可知,用力方向改为F2方向时,动力臂最长,根据杠杆平衡条件可知,动力臂越长、阻力臂越短,越省力,越有利于撬动石块。故A符合题意,BCD不符合题意。
故选A。
4.D
【详解】A.杠杆是一根能绕固定点转动的硬棒,这个固定点是杠杆的支点,支点一定在杠杆上,支点可以在杠杆的任意位置,故A错误;
B.省力杠杆可以省力,一定费距离,既省力又省距离的杠杆是不存在的,故B错误;
C.杠杆的长度和动力臂、阻力没有必然的联系,故C错误;
D.力臂是支点到力的作用线的距离,力臂可以在杠杆上,也可以不在杠杆上,故D正确。
故选D。
5.C
【详解】ABC.由图可知,杠杆绕O点转动,O点为支点,作用在M点向下的是动力,是手对筷子的力,作用在N点向上的力阻碍杠杆转动是阻力,阻力是食物对筷子的压力,分别从支点O向阻力作用线、动力作用线作垂线,就得到阻力臂ON,动力臂OM,故AB不符合题意,C符合题意;
D.把食物靠近支点放置时,阻力臂变小,阻力不变,阻力臂和阻力的乘积变小,动力臂不变,由杠杆平衡条件可知,动力变小,所以食指对筷子上M点的压力变小,故D不符合题意。
故选C。
6.A
【详解】由图甲可知,金属杆是粗细均匀的一只杠杆,绕点转动,金属杆的重心在杠杆的中点,阻力阻力臂为
用竖直向上的测力计拉着滑环缓慢向右移动时,滑环对金属杆的拉力等于测力计的拉力与滑环的重力之差,由图乙可知,当时,动力
则根据杠杆平衡的条件可得即┄┄①
当时,动力
则根据杠杆平衡的条件可得即┄┄②
解可得,
故A正确,BCD错误。
故选。
7.B
【详解】AB.增大物重时,阻力变大,由于动力和阻力臂不变,根据杠杆平衡条件:动力动力臂阻力阻力臂可知,应把动力臂变大,即把“權”向右端移,故A错误,B正确;
C.“權”小于物重时,动力小于阻力,根据杠杆平衡条件可知:当动力臂大于阻力臂时,杠杆可能在水平位置平衡,所以右端不一定上扬,故C错误;
D.若“權”发生磨损,动力变小,阻力不变,阻力臂不变,根据杠杆平衡条件可得,动力臂变大,即测量值比真实值偏大,故D错误。
故选B。
8.D
【详解】根据杠杆平衡原理可得
逆时针缓慢 转动30°角至水平位置动力臂l1不变,但是阻力臂l在不断的增大,故
成正比关系,故D符合题意,ABC不符合题意。
故选D。
9. 180 费力 大 见解析
【详解】[1][2]OB∶AB=2∶1,则OB∶OA=2∶3;杠杆水平平衡时,A端受到的阻力大小
FA=G物=120N,动力F的力臂为OB,阻力FA的力臂为OA,由杠杆平衡条件F1l1=F2l2可得F×OB=FA×OA
因为OB<OA,所以F>FA,即杠杆为费力杠杆。动力的大小为
[3][4]若其他条件不变,将F沿BC方向拉杠杆仍在水平位置平衡,拉力的力臂减小,阻力和阻力臂不变,根据杠杆的平衡条件F1l1=F2l2可知,拉力将变大。
10. 将重物远离甲同学 3:2
【详解】[1]由杠杆平衡条件得,要减轻甲同学的负担,即省力,要增大甲同学到支点O的距离,即增大动力臂,故要将重物远离甲同学。
[2]由得
11. 2.25 6 10
【详解】[1]两个质量均为50g的钩码的重力为:G=mg=0.1kg×10N/kg=1N
设杠杆上每个小格的长度为L;杠杆在水平位置平衡,根据杠杆的平衡条件可知FBLB=GLA
即FB×4L=1N×3L,解得F1=0.75N。物体的重力为G'=m'g=0.3kg×10N/kg=3N
物体受到竖直向下的重力、竖直向上的支持力和拉力的作用,根据平衡力和相互作用力可知地面对物体的支持力的大小为F支=G'-F1=3N-0.75N=2.25N
[2]要使物体对地面的压力大小为零,同时杠杆在水平位置平衡,此时物体对杠杆的拉力为3N;根据杠杆的平衡条件可知3N×4L=G"×3L
解得G"=4N;每个钩码的重力为0.5N;则A端所挂钩码的个数为
则加挂的钩码的个数Δn=8-2=6
[3]要使在A点所挂钩码的个数最多,钩码对杠杆的拉力的力臂不变,当弹簧测力计示数最大即弹簧测力计对杠杆拉力的力臂最大时,所挂钩码个数最大;弹簧测力计的最大称量值为3N,最大力臂为5L,根据杠杆的平衡条件可知3N×5L=GA×3L
解得GA=5N;每个钩码的重力为0.5N,则A点所挂钩码的最多个数为
12. 400 增大
【详解】[1]如图,杠杆的动力臂为4l,阻力臂为l,根据杠杆平衡条件可得,物体的重为
[2]若将拉力F沿逆时针方向转动60°,杠杆仍在水平位置平衡,此时阻力和阻力臂不变,动力臂变短,根据杠杆平衡条件可知,拉力将增大。
13. 0.75 2.25 225
【详解】[1]两个质量均为50g的钩码的质量为m=50g×2=100g=0.1kg
则两个钩码的重力为G=mg=0.1kg×10N/kg=1N
设杠杆上每个小格的长度为L;杠杆在水平位置平衡,由于杠杆的平衡条件F1L1=G1L2知道,即F1×4L=1N×3L解得F1=0.75N
[2]物体的重力为G'=m'g=0.3kg×10N/kg=3N
物体受到竖直向下的重力、竖直向上的支持力和拉力的作用,则地面对物体的支持力的大小为F支=G'﹣F1=3N﹣0.75N=2.25N
根据力的相互作用可知物体对地面压力的大小为F压=F支=2.25N
[3]物体对地面的压强
14. 10N 重心
【详解】[1]假设木棒的重心到B点的距离为OB,到A点的距离为OA,当在木棒左端以F1=4N的竖直向上的力刚好能提起木棒时,支点在A点,根据杠杆平衡的条件,则有
F1×AB=G×OA,当在木棒右端以F2=6N的竖直向上的力也能刚好提起木棒,支点在B点,根据杠杆平衡的条件,则有G×OB= F2×AB因为OA+OB=AB
这根木棒的重力为G=F1+F2=4N+6N=10N
[2]提高物体稳度有两种方法,分别是:增大支撑面积和降低重心。木棒平放在地面上远比竖起来要稳定,这是通过降低重心的方增大物体的稳定程度的。
15. 60 右 左
【详解】[1]由题意知,长为80cm的直杠杆,支点离右端20cm,支点离左端为80cm-20cm=60cm,杠杆左端的力臂长度l1=60cm,杠杆右端力臂的长度l2=20cm,根据杠杆平衡的条件,F1l1=F2l2可知,杠杆右端重物的重力为
[2]两端各加10N的重物后,杠杆左端G左l1=(20N+10N)×60cm=30N×60cm
杠杆右端G右l2=(60N+10N)×20cm=70N×20cm
由于G左l1>G右l2,杠杆的右端向上抬起。
[3]因为G左l1>G右l2,G左和G右是定值,只能减小l1,增大l2,将杠杆的支点向左移动。
16. 0.6 右
【详解】[1]由图中可知,该装置构成一个杠杆,支点为提扭1,动力F1等于秤砣重力,即F1=2N,秤砣与提纽1的水平距离为动力臂l1,即l1=15cm=0.15m
提纽1到秤盘的水平距离为阻力臂l2,即l2=5cm=0.05m
杆秤平衡时,由杠杆的平衡条件可得F1l1=F2l2
解得阻力为
物体的重力G物等于阻力F2,即G物=F2=6N
由G=mg可得,物体的质量为
[2]若小明用提纽2来测量该物体,可知阻力臂减小,而阻力不变,且动力也不变,故由杠杆的平衡条件可知,要使杆秤平衡,则动力臂应减小,即秤砣应向右移动。
17.
【详解】过支点做动力F1的垂线,则垂线段为力臂l1;连接OA,即为阻力臂,阻力F2垂直于阻力臂OA,由于阻力阻碍剪刀口闭合,所以力的方向向下,如下图所示:
18.
【详解】已知动力的作用点为M,则OM就是最长的动力臂,在阻力、阻力臂一定时,由杠杆平衡的条件F1l1=F2l2可知,此时动力最小,且方向垂直与力臂向下,据此画出最小的动力,如图所示:
19. 达到 右 直接在杠杆上读出力臂的大小 F1l1=F2l2 得到普遍规律 变大
【详解】(1)[1]挂钩码前,杠杆在如图甲所示的位置静止,因为杠杆处于静止状态,所以此时杠杆达到平衡状态。
[2]杠杆在如图甲所示的位置静止,左侧下沉,说明此时重心偏左,若要使杠杆在水平位置平衡,应将右端的平衡螺母向右调。
[3]调节杠杆在水平位置平衡,除了可以消除杠杆重力对实验的影响,在实验测量时还可以直接在杠杆上读出力臂的大小。
(2)[4]记录数据后,根据数据得出杠杆平衡条件F1l1=F2l2。
[5]进行多次实验,目的是得到普遍规律。
(3)[6]当测力计从a位置转动到b位置时,力臂变小,根据杠杆平衡条件可知,其示数大小将变大。
20.(1)4N;(2);(3)
【详解】解:(1)因为物体B浸没在水中
物体B受到的浮力
(2)物体B浸没在水中后液面上升的高度
物体B浸没在水中时容器中水深
物体B浸没在水中静止时,水对容器的压强
(3)物体A的重力
细线对杠杆的拉力为和
根据杠杆的平衡条件得
细线对B的拉力为
对物体B受力分析得
由得,物体B的质量
物体B的密度
答:(1)物体B受到的浮力4N;
(2)物体B浸没在水中静止时,水对容器底部的压强;
(3)细线对物体B的拉力及物体B的密度。
21.(1)1.8×103kg/m3;(2)16个水箱;(3)1.6m3
【详解】解:(1)该地板的底面积
地板的体积
地板的质量m=10.8kg,则地板的密度为
(2)设需要安装n个水箱;已知空水箱的质量为m0=450kg,每个水箱中水的质量m水=50kg,舞台和舞台架(不含水箱)的总质量为m台=10t=1×104kg,该舞台可以允许承受的演员和设备的总质量最大为m大=6t=6×103kg,则总质量为
总重力为
已知水箱的体积为1.5m3,当水箱的上表面与水面始终相平时,根据阿基米德原理可知,n个水箱悬浮时受到的浮力为
由于舞台漂浮在水面上,故F浮=G总,即
解得:n=16。
(3)A、B两端水箱提供的浮力大小均为
A、B两端水箱中水的重力为GA和GB,故A端水箱给舞台提供的支持力为
同理,B端水箱给舞台提供的支持力为
A的力臂为l1=25m,B的力臂l2=25m;C的重力
C的力臂为l3=20m;根据杠杆平衡条件可知,
即
解得
化简为
再次化简为
答:(1)该地板的密度是1.8×103kg/m3;
(2)若按照此要求设计舞台,至少需要安装16个水箱;
(3)V1和V2的差为1.6m3
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
