湖南省邵阳县黄亭市镇中学湘教版八年级数学上册教学课件:25全等三角形
文档属性
| 名称 | 湖南省邵阳县黄亭市镇中学湘教版八年级数学上册教学课件:25全等三角形 |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-16 14:01:03 | ||
图片预览






文档简介
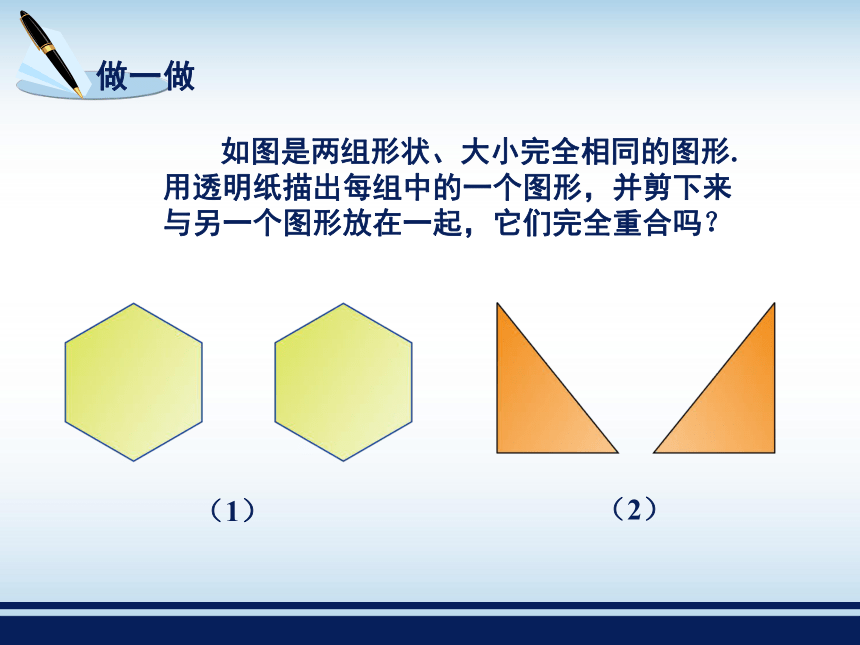
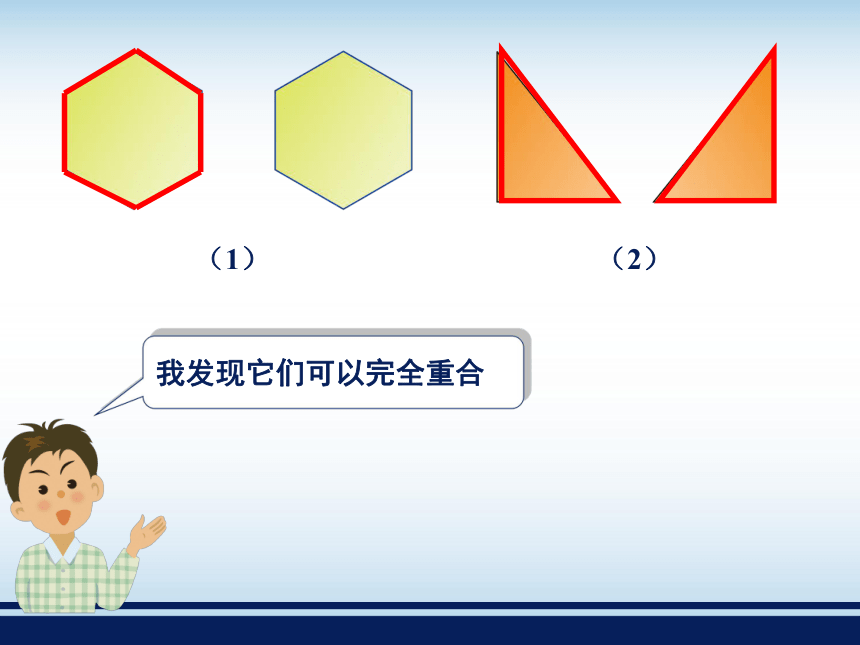
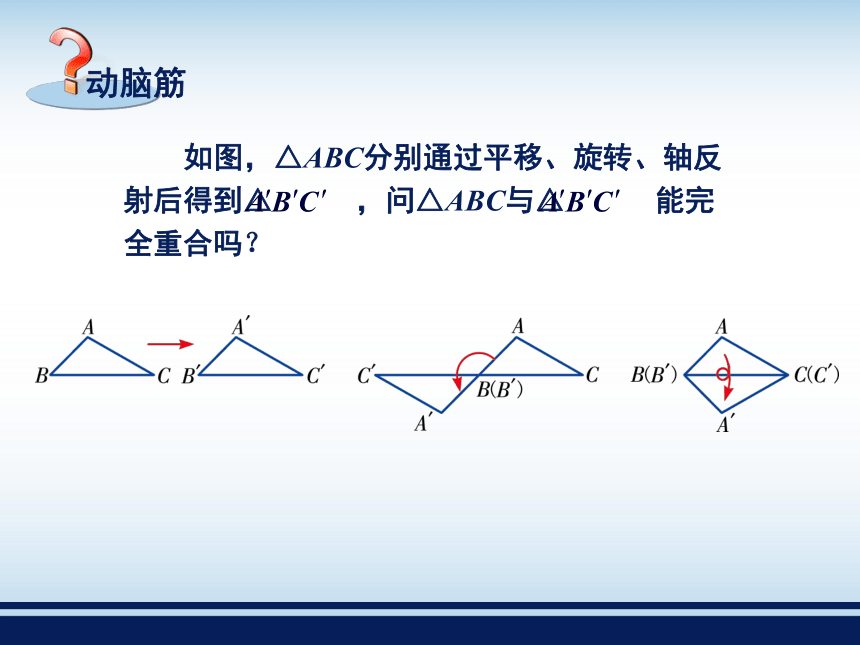
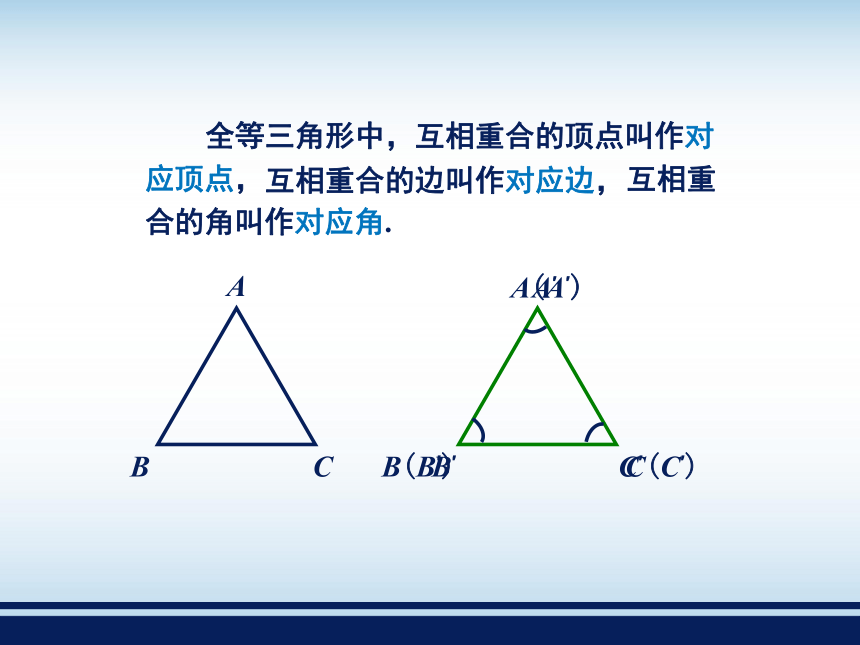
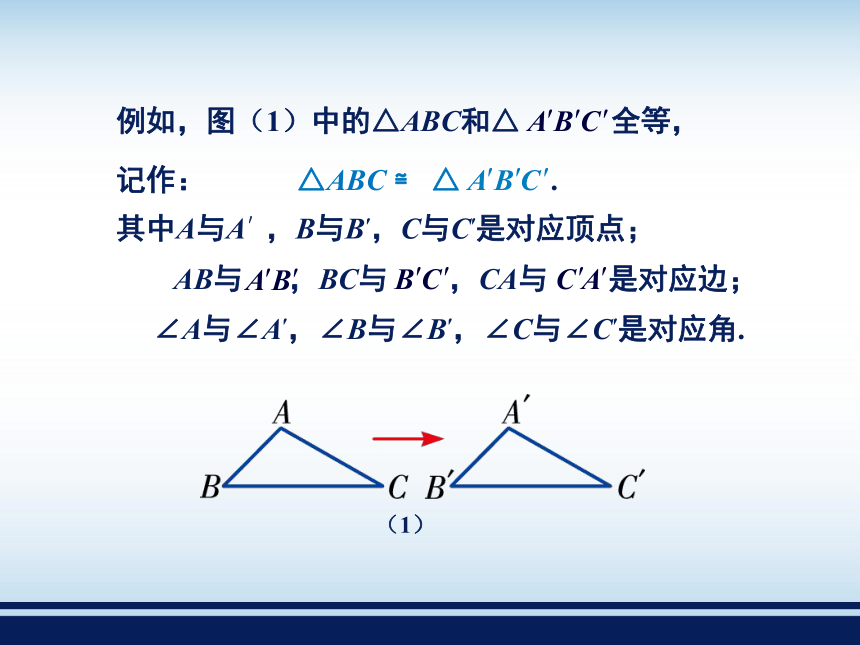
课件73张PPT。全等三角形2.5 如图是两组形状、大小完全相同的图形. 用透明纸描出每组中的一个图形,并剪下来与另一个图形放在一起,它们完全重合吗?我发现它们可以完全重合 我们把能够完全重合的两个图形叫作全等图形.能完全重合的两个三角形叫作全等三角形. 全等三角形中,互相重合的顶点叫作对应顶点, 互相重合的边叫作对应边, 互相重合的角叫作对应角.其中A与A′,B与B′,C与C′是对应顶点;∠A与∠A′,∠B与∠B′,∠C与∠C′是对应角. 全等用符号“≌”表示,读作“全等于”. 在表示两个三角形全等时,通常把表示对应顶点的字母写在对应位置上. 全等三角形的对应边相等; 全等三角形的对应角相等. 我们知道,能够完全重合的两条线段是相等的,能够完全重合的两个角是相等的,由此得到:例1 如图,已知△ABC≌△DCB,AB=3,
DB=4,∠A=60°.(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.解(1)AB与DC,AC与DB,BC与CB是对应边;∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角.∴ AC = DB = 4,
DC = AB =3.(2)∵ AC与DB,
AB与DC是全等三角形的对应边,∵∠A与∠D是全等三角形的对应角,∴∠D =∠A = 60°. 如图,已知△ADF≌△CBE,AD=4,BE=3,AF=6,∠A=20°,∠B=120°.(1)找出它们的所有对应边和对应角;
(2)求△ADF的周长及∠BEC的度数.解(1)AF与CE,AD与CB,DF与BE是对应边;∠A与∠C,∠AFD与∠CEB,∠D与∠B是对应角. (2)△ADF的周长是13,∠BEC=40°. 两个三角形满足什么条件就能全等呢?下面我们就来探讨这个问题. 每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论? 我发现它们完全重合,我猜测:有两边和它们的夹角分别相等的两个三角形全等. 下面,我们从以下这几种情形来探讨这个猜测是否为真.所以线段A″B″与 重合,由于旋转不改变图形的形状和大小,根据情形(1),(2)的结论得将△ABC作关于直线BC的轴反射,由于轴反射不改变图形的形状和大小,由此得到判定两个三角形全等的基本事实:
两边及其夹角分别相等的两个三角形全等.
通常可简写成“边角边”或“SAS”.例2 已知:如图,AB和CD相交于O,且AO=BO,
CO=DO. 求证:△ACO≌△BDO.∴ △ACO≌△BDO.(SAS)解 △ABO≌△A′B′O,∴AB= A′B′.2. 如图,AD∥BC,AD=BC. 问:△ADC和△CBA
是全等三角形吗?为什么?解 ∵ AD∥BC∴ △ADC≌△CBA. ∴∠DAC=∠BCA, 又 AD=BC,AC公共 3. 已知:如图,AB=AC,点E,F分别是AC,
AB的中点.
求证:BE=CF.解 ∵ AB=AC, 且 E,F分别是
AC,AB中点,∴ △ABE≌△ACF, ∴AF=AE, 又 ∠A公共,∴ BE=CF.由此得到判定两个三角形全等的基本事实:两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.例3 已知:如图,点A,F,E,C在同一条直线上,
AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.证明 ∵ AB∥DC,∴ ∠A=∠C.在△ABE和△CDF中,∴ △ABE≌△CDF (ASA).例4 如图,为测量河宽AB,小军从河岸的A点沿着和
AB垂直的方向走到C点,并在AC的中点E处立一
根标杆,然后从C点沿着与AC垂直的方向走到D
点,使D,E,B恰好在一条直线上. 于是小军
说:“CD的长就是河的宽.”你能说出这个道理吗?图3-35BECD∠A =∠C = 90°,AE = CE,∠AEB =∠CED (对顶角相等)∴ △AEB ≌ △CED.(ASA)∴ AB=CD .(全等三角形的对应边相等)因此,CD的长就是河的宽度.1. 如图,工人师傅不小心把一块三角形玻璃打碎
成三块,现要到玻璃店重新配一块与原来一样
的三角形玻璃,只允许带其中的一块玻璃碎片
去. 请问应带哪块玻璃碎片去?为什么?证明:
△ABC≌△A′B′C′, ∠A =∠A′ ,
∠ACB =∠A′C′B′.∴AC=A′C′证明:
∴ CF=C′F′. 又CF,C′F′分别是∠ACB和∠A′C′B′的平分线,∴ ∠ACF=∠A′C′F′.∴ △ACF≌△A′C′F′∵ ∠A = ∠A′,∠B = ∠B′,∴ ∠C =∠C′.由此得到判定两个三角形全等的定理: 两角分别相等且其中一组等角的对边相等的两个三角形全等.通常可简写成“角角边”或“AAS”.例5 已知:如图,∠B=∠D,∠1=∠2,
求证:△ABC≌△ADC.证明 ∵∠1 =∠2,∴∠ACB=∠ACD(同角的补角相等).在△ABC和△ADC中,∴ △ABC≌△ADC (AAS).例6 已知:如图,点B,F,C,E在同一条直线上,
AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF.证明 ∵ AC∥FD,∴∠ACB =∠DFE.∵ BF= EC,∴ BF+FC=EC+FC,即 BC=EF .在△ABC 和△DEF中,∴ △ABC≌△DEF(AAS).1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC≌△AEB.∴ △ADC≌△AEB(AAS).2. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.证明 由题意可知△BEC和△BDC均为直角三角形,∵ 在Rt△BEC和Rt△CDB中,∠ABC =∠ACB ,BC = BC ,∴ Rt△BEC≌ Rt△CDB(AAS).∠BEC =∠CDB=90° , 如图,在△ABC和 中,如果 ,
, ,那么△ABC与 全等吗? 由上述变换性质可知△ABC ≌ ,∴ ∠1=∠2,∠3=∠4.从而∠1+∠3=∠2+∠4,由此可以得到判定两个三角形全等的基本事实:三边分别相等的两个三角形全等.通常可简写成“边边边”或“SSS”.例7 已知:如图,AB=CD ,BC=DA.
求证: ∠B=∠D.∴ △ABC ≌△CDA. (SSS)∴ ∠B =∠D.例8 已知:如图,在△ABC中,AB=AC,点D,E
在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.证明 ∵ BE = CD,∴ BE-DE = CD-DE.即 BD = CE.在△ABD和△ACE中,∴ △ABD≌△ACE (SSS). 由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性. 三角形的稳定性在生产和生活中有广泛的应用. 如日常生活中的定位锁、房屋的人字梁屋顶等都采用三角形结构,其道理就是运用三角形的稳定性.1. 如图,已知AD=BC,AC=BD.
那么∠1与∠2相等吗?答:相等.
因为 AD=BC,
AC=BD,
AB公共,
所以△ABD≌△BAC (SSS).
所以∠1 =∠2 (全等三角形对应角相等).2. 如图,点A,C,B,D在同一条直线上,
AC=BD,AE=CF,BE=DF.
求证:AE∥CF,BE∥DF.证明 ∵ AC=BD,∴ AC+BC=BD+BC ,即 AB=CD .所以 AE∥CF,BE∥DF.又 AE=CF,BE=DF,所以 △ABE≌△CDF (SSS).
所以 ∠EAB =∠FCD, ∠EBA =∠FDC (全等三角形对应角相等). 满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论? 满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.(2) ∠A=∠A′= 80°,∠B=∠B′= 30°,
∠C=∠C′=70°. 满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论? 满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.例9 已知:如图,AC与BD相交于点O,
且AB= DC,AC = DB.
求证:∠A =∠D.证明 连接BC.在△ABC和△DCB中,∴ △ABC ≌△DCB (SSS).∴ ∠A =∠D.例10 某地在山区修建高速公路时需挖通一条隧道.
为估测这条隧道的长度(如图),需测出这
座山A,B间的距离,结合所学知识,你能给
出什么好方法吗?解 选择某一合适的地点O,使得从O点能测出AO与BO的长度. 这样就构造出两个三角形.OA′B′1. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.证明 如图,连接AC.所以 △ACB≌△ ACD (SSS).所以 ∠B =∠D.2. 如图,在△ABC和△DEC中,已知一些相等的边
或角(见下表),请再补充适当的条件,从而能
运用已学的判定方法来判定△ABC≌△DEC.AB=DE∠B=∠E∠ACB=∠DCEBC=EC 如图,在△ABC与△DEF中,已知条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( ).
A.∠B=∠E,BC=EF B. BC=EF,AC=DF
C. ∠A=∠D,∠B=∠E D. ∠A=∠D,BC=EF例1 D例2 如图4.2-2,△ACB≌ ,∠BCB′=30°,则∠ACA′的度数为( ).
A.20° B. 30° C. 35° D. 40°B结 束
DB=4,∠A=60°.(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.解(1)AB与DC,AC与DB,BC与CB是对应边;∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角.∴ AC = DB = 4,
DC = AB =3.(2)∵ AC与DB,
AB与DC是全等三角形的对应边,∵∠A与∠D是全等三角形的对应角,∴∠D =∠A = 60°. 如图,已知△ADF≌△CBE,AD=4,BE=3,AF=6,∠A=20°,∠B=120°.(1)找出它们的所有对应边和对应角;
(2)求△ADF的周长及∠BEC的度数.解(1)AF与CE,AD与CB,DF与BE是对应边;∠A与∠C,∠AFD与∠CEB,∠D与∠B是对应角. (2)△ADF的周长是13,∠BEC=40°. 两个三角形满足什么条件就能全等呢?下面我们就来探讨这个问题. 每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论? 我发现它们完全重合,我猜测:有两边和它们的夹角分别相等的两个三角形全等. 下面,我们从以下这几种情形来探讨这个猜测是否为真.所以线段A″B″与 重合,由于旋转不改变图形的形状和大小,根据情形(1),(2)的结论得将△ABC作关于直线BC的轴反射,由于轴反射不改变图形的形状和大小,由此得到判定两个三角形全等的基本事实:
两边及其夹角分别相等的两个三角形全等.
通常可简写成“边角边”或“SAS”.例2 已知:如图,AB和CD相交于O,且AO=BO,
CO=DO. 求证:△ACO≌△BDO.∴ △ACO≌△BDO.(SAS)解 △ABO≌△A′B′O,∴AB= A′B′.2. 如图,AD∥BC,AD=BC. 问:△ADC和△CBA
是全等三角形吗?为什么?解 ∵ AD∥BC∴ △ADC≌△CBA. ∴∠DAC=∠BCA, 又 AD=BC,AC公共 3. 已知:如图,AB=AC,点E,F分别是AC,
AB的中点.
求证:BE=CF.解 ∵ AB=AC, 且 E,F分别是
AC,AB中点,∴ △ABE≌△ACF, ∴AF=AE, 又 ∠A公共,∴ BE=CF.由此得到判定两个三角形全等的基本事实:两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.例3 已知:如图,点A,F,E,C在同一条直线上,
AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.证明 ∵ AB∥DC,∴ ∠A=∠C.在△ABE和△CDF中,∴ △ABE≌△CDF (ASA).例4 如图,为测量河宽AB,小军从河岸的A点沿着和
AB垂直的方向走到C点,并在AC的中点E处立一
根标杆,然后从C点沿着与AC垂直的方向走到D
点,使D,E,B恰好在一条直线上. 于是小军
说:“CD的长就是河的宽.”你能说出这个道理吗?图3-35BECD∠A =∠C = 90°,AE = CE,∠AEB =∠CED (对顶角相等)∴ △AEB ≌ △CED.(ASA)∴ AB=CD .(全等三角形的对应边相等)因此,CD的长就是河的宽度.1. 如图,工人师傅不小心把一块三角形玻璃打碎
成三块,现要到玻璃店重新配一块与原来一样
的三角形玻璃,只允许带其中的一块玻璃碎片
去. 请问应带哪块玻璃碎片去?为什么?证明:
△ABC≌△A′B′C′, ∠A =∠A′ ,
∠ACB =∠A′C′B′.∴AC=A′C′证明:
∴ CF=C′F′. 又CF,C′F′分别是∠ACB和∠A′C′B′的平分线,∴ ∠ACF=∠A′C′F′.∴ △ACF≌△A′C′F′∵ ∠A = ∠A′,∠B = ∠B′,∴ ∠C =∠C′.由此得到判定两个三角形全等的定理: 两角分别相等且其中一组等角的对边相等的两个三角形全等.通常可简写成“角角边”或“AAS”.例5 已知:如图,∠B=∠D,∠1=∠2,
求证:△ABC≌△ADC.证明 ∵∠1 =∠2,∴∠ACB=∠ACD(同角的补角相等).在△ABC和△ADC中,∴ △ABC≌△ADC (AAS).例6 已知:如图,点B,F,C,E在同一条直线上,
AC∥FD,∠A=∠D,BF=EC.
求证:△ABC≌△DEF.证明 ∵ AC∥FD,∴∠ACB =∠DFE.∵ BF= EC,∴ BF+FC=EC+FC,即 BC=EF .在△ABC 和△DEF中,∴ △ABC≌△DEF(AAS).1. 已知:如图,∠1=∠2,AD=AE.
求证:△ADC≌△AEB.∴ △ADC≌△AEB(AAS).2. 已知:在△ABC中,∠ABC =∠ACB,
BD⊥AC于点D,CE⊥AB于点E.
求证:BD=CE.证明 由题意可知△BEC和△BDC均为直角三角形,∵ 在Rt△BEC和Rt△CDB中,∠ABC =∠ACB ,BC = BC ,∴ Rt△BEC≌ Rt△CDB(AAS).∠BEC =∠CDB=90° , 如图,在△ABC和 中,如果 ,
, ,那么△ABC与 全等吗? 由上述变换性质可知△ABC ≌ ,∴ ∠1=∠2,∠3=∠4.从而∠1+∠3=∠2+∠4,由此可以得到判定两个三角形全等的基本事实:三边分别相等的两个三角形全等.通常可简写成“边边边”或“SSS”.例7 已知:如图,AB=CD ,BC=DA.
求证: ∠B=∠D.∴ △ABC ≌△CDA. (SSS)∴ ∠B =∠D.例8 已知:如图,在△ABC中,AB=AC,点D,E
在BC上,且AD=AE,BE=CD.
求证:△ABD≌△ACE.证明 ∵ BE = CD,∴ BE-DE = CD-DE.即 BD = CE.在△ABD和△ACE中,∴ △ABD≌△ACE (SSS). 由“边边边”可知,只要三角形三边的长度确定,那么这个三角形的形状和大小也就固定了,三角形的这个性质叫作三角形的稳定性. 三角形的稳定性在生产和生活中有广泛的应用. 如日常生活中的定位锁、房屋的人字梁屋顶等都采用三角形结构,其道理就是运用三角形的稳定性.1. 如图,已知AD=BC,AC=BD.
那么∠1与∠2相等吗?答:相等.
因为 AD=BC,
AC=BD,
AB公共,
所以△ABD≌△BAC (SSS).
所以∠1 =∠2 (全等三角形对应角相等).2. 如图,点A,C,B,D在同一条直线上,
AC=BD,AE=CF,BE=DF.
求证:AE∥CF,BE∥DF.证明 ∵ AC=BD,∴ AC+BC=BD+BC ,即 AB=CD .所以 AE∥CF,BE∥DF.又 AE=CF,BE=DF,所以 △ABE≌△CDF (SSS).
所以 ∠EAB =∠FCD, ∠EBA =∠FDC (全等三角形对应角相等). 满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论? 满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.(2) ∠A=∠A′= 80°,∠B=∠B′= 30°,
∠C=∠C′=70°. 满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论? 满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.例9 已知:如图,AC与BD相交于点O,
且AB= DC,AC = DB.
求证:∠A =∠D.证明 连接BC.在△ABC和△DCB中,∴ △ABC ≌△DCB (SSS).∴ ∠A =∠D.例10 某地在山区修建高速公路时需挖通一条隧道.
为估测这条隧道的长度(如图),需测出这
座山A,B间的距离,结合所学知识,你能给
出什么好方法吗?解 选择某一合适的地点O,使得从O点能测出AO与BO的长度. 这样就构造出两个三角形.OA′B′1. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.证明 如图,连接AC.所以 △ACB≌△ ACD (SSS).所以 ∠B =∠D.2. 如图,在△ABC和△DEC中,已知一些相等的边
或角(见下表),请再补充适当的条件,从而能
运用已学的判定方法来判定△ABC≌△DEC.AB=DE∠B=∠E∠ACB=∠DCEBC=EC 如图,在△ABC与△DEF中,已知条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( ).
A.∠B=∠E,BC=EF B. BC=EF,AC=DF
C. ∠A=∠D,∠B=∠E D. ∠A=∠D,BC=EF例1 D例2 如图4.2-2,△ACB≌ ,∠BCB′=30°,则∠ACA′的度数为( ).
A.20° B. 30° C. 35° D. 40°B结 束
同课章节目录
