专题08 二次函数与一元二次方程、不等式-【夯实基础】2023-2024高一数学同步限时训练(人教A版2019必修第一册)(含解析)
文档属性
| 名称 | 专题08 二次函数与一元二次方程、不等式-【夯实基础】2023-2024高一数学同步限时训练(人教A版2019必修第一册)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 08:49:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【夯实基础】2023-2024高一数学同步限时训练(新人教A版2019)专题08 二次函数与一元二次方程、不等式
一、单选题
1.(2023·全国·高一假期作业)不等式的解集为( )
A. B.
C. D.
2.(2023·全国·高一假期作业)关于x的不等式的解集为( )
A.
B.
C.
D.
3.(2023·全国·高一假期作业)若不等式的解集为,则函数的图象与x轴的交点为( )
A.和 B.
C. D.和
4.(2023·全国·高一假期作业)若不等式对任意实数x恒成立,则实数a的取值范围为( )
A. B.
C. D.
5.(2023·全国·高一假期作业)已知不等式对任意实数恒成立,则的取值范围是( )
A. B.
C.或 D.
6.(2022秋·湖南郴州·高一校考阶段练习)不等式的解集为( )
A. B. C. D.或
7.(2022秋·河南郑州·高一校考阶段练习)不等式的解集为( )
A.或 B.
C.或 D.
8.(2022秋·云南楚雄·高一校考阶段练习)不等式的解集为,则的值为 ( )
A.-2 B.0 C.2 D.5
9.(2023·全国·高一假期作业)若不等式对于恒成立,则实数a的取值范围是( )
A. B. C. D.
10.(2023春·福建莆田·高二莆田第二十五中学校考期中)若二次函数的图像都在轴下方,则实数的取值范围为( )
A. B. C. D.
11.(2023秋·湖南长沙·高一统考期末)某小型服装厂生产一种风衣,日销售量x(件)与单价P(元)之间的关系为,生产x件所需成本为C(元),其中元,若要求每天获利不少于1300元,则日销量x的取值范围是( )
A.20≤x≤30 B.20≤x≤45
C.15≤x≤30 D.15≤x≤45
12.(2023·全国·高一假期作业)不等式的解集是( )
A. B. C. D.
13.(2023·全国·高一假期作业)不等式的解集是( )
A. B.
C.或 D.
14.(2023·全国·高一假期作业)若一元二次不等式的解集是,则一元二次不等式的解集是( )
A. B.
C. D.
15.(2023·全国·高一假期作业)某文具店购进一批新型台灯,每盏的最低售价为15元,若每盏按最低售价销售,每天能卖出45盏,每盏售价每提高1元,日销售量将减少3盏,为了使这批台灯每天获得600元以上的销售收入,则这批台灯的销售单价x(单位:元)的取值范围是( )
A. B. C. D.
二、多选题
16.(2023·全国·高一假期作业)有纯农药液一桶,倒出8升后用水加满,然后又倒出4升后再用水加满,此时桶中所含的纯农药药液不超过桶的容积的,则桶的容积可能为( )
A.7 B.9 C.11 D.13
17.(2023春·内蒙古呼和浩特·高一统考阶段练习)已知关于x的不等式的解集为,则下列说法中正确的有( )
A. B.
C. D.
三、填空题
18.(2023·全国·高一假期作业) 的解集为___________________.
19.(2023·全国·高一假期作业)当时,关于x的不等式的解集是__________.
20.(2019秋·陕西咸阳·高二统考期末)若一元二次不等式的解集是,则的值是_____.
21.(2023·全国·高一假期作业)若不等式的解集为R,则实数的取值范围是________.
22.(2021秋·上海嘉定·高一上海市嘉定区第一中学校考期中)某地每年销售木材约万m3,每立方米的价格为元.为了减少木材消耗,决定按销售收入的征收木材税,这样每年的木材销售量减少万m3,为了既减少了木材消耗又保证税金收入每年不少于万元,则的取值范围是________.
四、解答题
23.(2022秋·上海虹口·高一上海市复兴高级中学校考期中)解关于x的不等式.
24.(2023·全国·高一假期作业)已知不等式的解集是,求a,c的值.
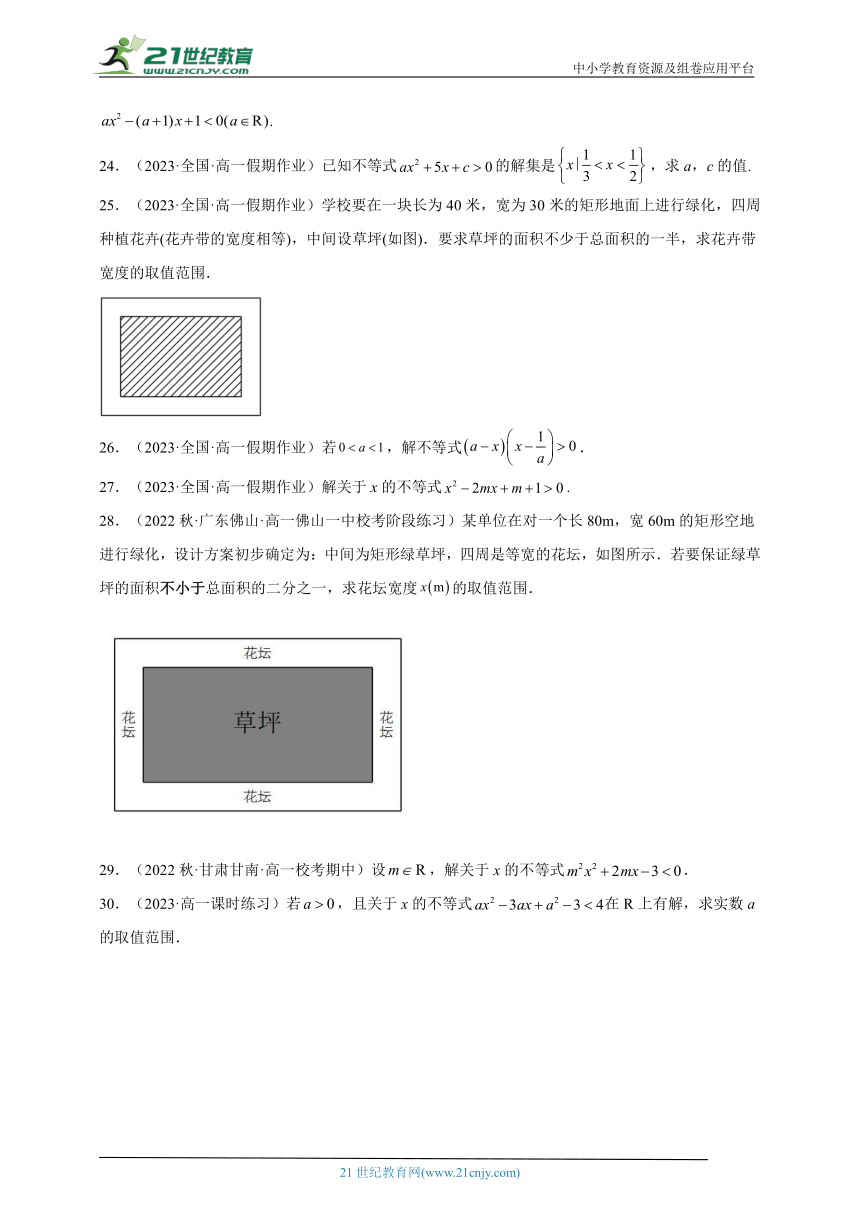
25.(2023·全国·高一假期作业)学校要在一块长为40米,宽为30米的矩形地面上进行绿化,四周种植花卉(花卉带的宽度相等),中间设草坪(如图).要求草坪的面积不少于总面积的一半,求花卉带宽度的取值范围.
26.(2023·全国·高一假期作业)若,解不等式.
27.(2023·全国·高一假期作业)解关于x的不等式.
28.(2022秋·广东佛山·高一佛山一中校考阶段练习)某单位在对一个长80m,宽60m的矩形空地进行绿化,设计方案初步确定为:中间为矩形绿草坪,四周是等宽的花坛,如图所示.若要保证绿草坪的面积不小于总面积的二分之一,求花坛宽度的取值范围.
29.(2022秋·甘肃甘南·高一校考期中)设,解关于x的不等式.
30.(2023·高一课时练习)若,且关于x的不等式在R上有解,求实数a的取值范围.
参考答案:
1.A
【分析】先移项,再提取公因式,即得不等式的解集.
【详解】不等式可化为,
解得,
即不等式的解集为.
故选:A
2.D
【分析】直接解一元二次不等式即可得到答案.
【详解】不等式可化为.
∵,∴.
∴原不等式的解集为.
故选:D
3.A
【分析】不等式的解集为,可得方程的两个根为,利用根与系数的关系可得,即可得出结果.
【详解】若不等式的解集为,
则方程的两个根为且,
,解得,
则函数,
令,解得或,
故函数的图象与轴的交点为和.
故选:A.
4.A
【分析】求出二次函数的最小值,从而可得关于的不等式,求出其解后可得其取值范围.
【详解】,当且仅当时等号成立,
故,故,
故选:A.
5.D
【分析】分和,结合二次函数的图象分析得解.
【详解】① 若,则恒成立,满足题意;
② ,则,
, ∴.
综上所述.
故选:D
6.C
【分析】利用一元二次不等式的解法解原不等式,可得其解集.
【详解】解不等式可得,故原不等式的解集为.
故选:C.
7.B
【分析】化简原不等式,利用一元二次不等式的解法解原不等式即可.
【详解】原不等式即为,解得,
故原不等式的解集为.
故选 :B.
8.C
【分析】根据题意,利用方程根与系数的关系求解.
【详解】解:因为不等式的解集为,
所以,解得 ,
所以 ,
故选:C
9.C
【分析】原不等式可化为,设.只需求出在时的最小值,即可得出答案.
【详解】原不等式可化为,
设,
则,
当且仅当,且,即时,函数有最小值为2.
因为恒成立,所以.
故选:C.
10.A
【分析】二次函数必须满足二次项系数,其次恒成立可利用二次不等式在上恒成立的处理方法来做即可.
【详解】由于是二次函数,则二次项系数,依题意,对于恒成立,则二次函数开口必然向下,且和轴没有交点,即,解得.
故选:A
11.B
【分析】根据已知条件,先求出该厂每天获得的利润的函数解析式,再结合每天获利不少于1300元,列出不等式求解即可.
【详解】设该厂每天获得的利润为y元,
则y=(160-2x)x-(500+30x)=-2x2+130x-500(0<x<80).
由题意,知-2x2+130x-500≥1300,即x2-65x+900≤0,解得:20≤x≤45,
所以日销量x的取值范围是20≤x≤45.
故选:B.
12.C
【分析】由因式分解结合一元二次不等式的解的特征即可求解.
【详解】由得,解得或,
故不等式的解为,
故选:C
13.D
【分析】将不等式化为再解一元二次不等式可得答案.
【详解】将不等式化为,由于对应方程的判别式,
所以不等式的解集为.
故选:D.
14.C
【分析】由题意可得是的两个根,且利用韦达定理可得到,即可对进行求解
【详解】由一元二次不等式的解集是可得是的两个根,且
所以,
所以可化为,即,
解得或.
故选:C
15.B
【分析】由题意为了使这批台灯每天获得600元以上的销售收入,
可列不等式 同时需要注意最低售价为15元,即.同时满足上述条件,可解得范围得到答案
【详解】由题意,得,即,∴,解得.又每盏的最低售价为15元,∴.
故选:B.
16.BC
【分析】根据题意列出不等式求解即可.
【详解】设桶的容积为x,
根据题意可得关于x的一元二次不等式:,且,
化简可得,
,
故选:BC
17.ABC
【分析】根据二次不等式解集可知,且方程的两根分别为2,3,结合韦达定理可得之间的等量关系,分别代入各个选项即可得出结果.
【详解】解:因为的解集为,
所以,且方程的两根分别为2,3,
由韦达定理可知:,结合,
解得,所以,
所以选项A、B正确;
因为,所以选项C正确;
因为,所以选项D错误.
故选:ABC
18.或
【分析】化简原不等式为,即得解.
【详解】因为,
所以,
即,
所以或.
所以不等式的解集为或.
故答案为:或
19.或
【分析】判断的大小,即可求解不等式的解集.
【详解】∵,∴,
由得或,
故不等式的解集是或,
故答案为:或
20.
【分析】由题得,计算即得解.
【详解】一元二次不等式的解集是,
则和是一元二次方程的实数根,
∴, 解得.
故答案为:
21.
【分析】对不等式的类型分类讨论,根据判别式及二次项系数的符号列式可求出结果.
【详解】①当,即时,
,解得.
②当,即时,
若,则原不等式为,恒成立.
若,则原不等式为,即,不符合题目要求,舍去.
综上所述,当时,原不等式的解集为R.
故答案为:.
22.
【分析】根据题意列式,解不等式可得结果.
【详解】设按销售收入的征收木材税时,税金收入为万元,
则,
令,即,解得.
故答案为:
23.答案见解析
【分析】对不等式变形为,然后对进行合理分类讨论即可.
【详解】原不等式变为,
①当时,原不等式可化为,
所以当时,解得;
当时,解集为;
当时,解得
②当时,原不等式等价于,即.
③当时,,原不等式可化为,
解得或.
综上,当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为或.
24.
【分析】由一元二次不等式的解与二次方程的根之间关系,由韦达定理即可求解.
【详解】由于不等式的解集是,所以和是的两个根,由韦达定理可得且,解得,
25.花卉带宽度的取值范围为(单位:米)
【分析】设花卉带的宽度为米,则草坪的长和宽分别是米,米,由面积关系列不等式,化简后解一元二次不等式得答案.
【详解】设花卉带的宽度为米,则草坪的长和宽分别是米,米,
则,所以,解得
故花卉带宽度的取值范围为(单位:米).
26.
【分析】根据题意,,转化不等式,求解即可.
【详解】解:∵,∴,
原不等式可化为,
解得.
故原不等式的解集为.
27.答案见解析
【分析】分类讨论判别式,确定一元二次不等式对应方程解的情况,即可求得答案.
【详解】不等式对应方程的判别式,
(1)当,即或时,
由于方程的根是,
所以不等式的解集是或};
(2)当,即时,不等式的解集为且;
(3)当,即时,不等式的解集为R,
故或时,不等式的解集是或};
时,不等式的解集为且;
时,不等式的解集为R.
28.
【分析】首先表示出绿草坪的长、宽,即可得到草坪的面积,依题意得到关于的一元二次不等式,解得即可.
【详解】解:花坛的宽度为,所以绿草坪的长为,宽为,
草坪面积为,
总面积,
根据题意可得,
整理得,解得或.
由题意知,解得,所以不符合题意,舍去,
所以.
答:当时,绿草坪的面积不小于总面积的二分之一.
29.当时,不等式解集为,
当时,原不等式的解集为,
当时,原不等式的解集为.
【分析】由二次不等式的解法,注意分类讨论即可.
【详解】因为,所以:①当时,原不等式变为:恒成立,所以此时解集为;
②当时,,则不等式得,
则对应方程的根为:,
当时,原不等式的解集为,
当时,原不等式的解集为.
综上:当时,不等式解集为,
当时,原不等式的解集为,
当时,原不等式的解集为.
30.
【分析】根据二次不等式的解法即得;或参变分离,求函数的最值即得.
【详解】方法一(判别式法)关于x的不等式可变形为,
由题可得,
解得,
又,
所以实数a的取值范围为;
方法二(分离变量法)因为,所以关于x的不等式可变形为,
因为,
所以,解得,
又,所以实数a的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【夯实基础】2023-2024高一数学同步限时训练(新人教A版2019)专题08 二次函数与一元二次方程、不等式
一、单选题
1.(2023·全国·高一假期作业)不等式的解集为( )
A. B.
C. D.
2.(2023·全国·高一假期作业)关于x的不等式的解集为( )
A.
B.
C.
D.
3.(2023·全国·高一假期作业)若不等式的解集为,则函数的图象与x轴的交点为( )
A.和 B.
C. D.和
4.(2023·全国·高一假期作业)若不等式对任意实数x恒成立,则实数a的取值范围为( )
A. B.
C. D.
5.(2023·全国·高一假期作业)已知不等式对任意实数恒成立,则的取值范围是( )
A. B.
C.或 D.
6.(2022秋·湖南郴州·高一校考阶段练习)不等式的解集为( )
A. B. C. D.或
7.(2022秋·河南郑州·高一校考阶段练习)不等式的解集为( )
A.或 B.
C.或 D.
8.(2022秋·云南楚雄·高一校考阶段练习)不等式的解集为,则的值为 ( )
A.-2 B.0 C.2 D.5
9.(2023·全国·高一假期作业)若不等式对于恒成立,则实数a的取值范围是( )
A. B. C. D.
10.(2023春·福建莆田·高二莆田第二十五中学校考期中)若二次函数的图像都在轴下方,则实数的取值范围为( )
A. B. C. D.
11.(2023秋·湖南长沙·高一统考期末)某小型服装厂生产一种风衣,日销售量x(件)与单价P(元)之间的关系为,生产x件所需成本为C(元),其中元,若要求每天获利不少于1300元,则日销量x的取值范围是( )
A.20≤x≤30 B.20≤x≤45
C.15≤x≤30 D.15≤x≤45
12.(2023·全国·高一假期作业)不等式的解集是( )
A. B. C. D.
13.(2023·全国·高一假期作业)不等式的解集是( )
A. B.
C.或 D.
14.(2023·全国·高一假期作业)若一元二次不等式的解集是,则一元二次不等式的解集是( )
A. B.
C. D.
15.(2023·全国·高一假期作业)某文具店购进一批新型台灯,每盏的最低售价为15元,若每盏按最低售价销售,每天能卖出45盏,每盏售价每提高1元,日销售量将减少3盏,为了使这批台灯每天获得600元以上的销售收入,则这批台灯的销售单价x(单位:元)的取值范围是( )
A. B. C. D.
二、多选题
16.(2023·全国·高一假期作业)有纯农药液一桶,倒出8升后用水加满,然后又倒出4升后再用水加满,此时桶中所含的纯农药药液不超过桶的容积的,则桶的容积可能为( )
A.7 B.9 C.11 D.13
17.(2023春·内蒙古呼和浩特·高一统考阶段练习)已知关于x的不等式的解集为,则下列说法中正确的有( )
A. B.
C. D.
三、填空题
18.(2023·全国·高一假期作业) 的解集为___________________.
19.(2023·全国·高一假期作业)当时,关于x的不等式的解集是__________.
20.(2019秋·陕西咸阳·高二统考期末)若一元二次不等式的解集是,则的值是_____.
21.(2023·全国·高一假期作业)若不等式的解集为R,则实数的取值范围是________.
22.(2021秋·上海嘉定·高一上海市嘉定区第一中学校考期中)某地每年销售木材约万m3,每立方米的价格为元.为了减少木材消耗,决定按销售收入的征收木材税,这样每年的木材销售量减少万m3,为了既减少了木材消耗又保证税金收入每年不少于万元,则的取值范围是________.
四、解答题
23.(2022秋·上海虹口·高一上海市复兴高级中学校考期中)解关于x的不等式.
24.(2023·全国·高一假期作业)已知不等式的解集是,求a,c的值.
25.(2023·全国·高一假期作业)学校要在一块长为40米,宽为30米的矩形地面上进行绿化,四周种植花卉(花卉带的宽度相等),中间设草坪(如图).要求草坪的面积不少于总面积的一半,求花卉带宽度的取值范围.
26.(2023·全国·高一假期作业)若,解不等式.
27.(2023·全国·高一假期作业)解关于x的不等式.
28.(2022秋·广东佛山·高一佛山一中校考阶段练习)某单位在对一个长80m,宽60m的矩形空地进行绿化,设计方案初步确定为:中间为矩形绿草坪,四周是等宽的花坛,如图所示.若要保证绿草坪的面积不小于总面积的二分之一,求花坛宽度的取值范围.
29.(2022秋·甘肃甘南·高一校考期中)设,解关于x的不等式.
30.(2023·高一课时练习)若,且关于x的不等式在R上有解,求实数a的取值范围.
参考答案:
1.A
【分析】先移项,再提取公因式,即得不等式的解集.
【详解】不等式可化为,
解得,
即不等式的解集为.
故选:A
2.D
【分析】直接解一元二次不等式即可得到答案.
【详解】不等式可化为.
∵,∴.
∴原不等式的解集为.
故选:D
3.A
【分析】不等式的解集为,可得方程的两个根为,利用根与系数的关系可得,即可得出结果.
【详解】若不等式的解集为,
则方程的两个根为且,
,解得,
则函数,
令,解得或,
故函数的图象与轴的交点为和.
故选:A.
4.A
【分析】求出二次函数的最小值,从而可得关于的不等式,求出其解后可得其取值范围.
【详解】,当且仅当时等号成立,
故,故,
故选:A.
5.D
【分析】分和,结合二次函数的图象分析得解.
【详解】① 若,则恒成立,满足题意;
② ,则,
, ∴.
综上所述.
故选:D
6.C
【分析】利用一元二次不等式的解法解原不等式,可得其解集.
【详解】解不等式可得,故原不等式的解集为.
故选:C.
7.B
【分析】化简原不等式,利用一元二次不等式的解法解原不等式即可.
【详解】原不等式即为,解得,
故原不等式的解集为.
故选 :B.
8.C
【分析】根据题意,利用方程根与系数的关系求解.
【详解】解:因为不等式的解集为,
所以,解得 ,
所以 ,
故选:C
9.C
【分析】原不等式可化为,设.只需求出在时的最小值,即可得出答案.
【详解】原不等式可化为,
设,
则,
当且仅当,且,即时,函数有最小值为2.
因为恒成立,所以.
故选:C.
10.A
【分析】二次函数必须满足二次项系数,其次恒成立可利用二次不等式在上恒成立的处理方法来做即可.
【详解】由于是二次函数,则二次项系数,依题意,对于恒成立,则二次函数开口必然向下,且和轴没有交点,即,解得.
故选:A
11.B
【分析】根据已知条件,先求出该厂每天获得的利润的函数解析式,再结合每天获利不少于1300元,列出不等式求解即可.
【详解】设该厂每天获得的利润为y元,
则y=(160-2x)x-(500+30x)=-2x2+130x-500(0<x<80).
由题意,知-2x2+130x-500≥1300,即x2-65x+900≤0,解得:20≤x≤45,
所以日销量x的取值范围是20≤x≤45.
故选:B.
12.C
【分析】由因式分解结合一元二次不等式的解的特征即可求解.
【详解】由得,解得或,
故不等式的解为,
故选:C
13.D
【分析】将不等式化为再解一元二次不等式可得答案.
【详解】将不等式化为,由于对应方程的判别式,
所以不等式的解集为.
故选:D.
14.C
【分析】由题意可得是的两个根,且利用韦达定理可得到,即可对进行求解
【详解】由一元二次不等式的解集是可得是的两个根,且
所以,
所以可化为,即,
解得或.
故选:C
15.B
【分析】由题意为了使这批台灯每天获得600元以上的销售收入,
可列不等式 同时需要注意最低售价为15元,即.同时满足上述条件,可解得范围得到答案
【详解】由题意,得,即,∴,解得.又每盏的最低售价为15元,∴.
故选:B.
16.BC
【分析】根据题意列出不等式求解即可.
【详解】设桶的容积为x,
根据题意可得关于x的一元二次不等式:,且,
化简可得,
,
故选:BC
17.ABC
【分析】根据二次不等式解集可知,且方程的两根分别为2,3,结合韦达定理可得之间的等量关系,分别代入各个选项即可得出结果.
【详解】解:因为的解集为,
所以,且方程的两根分别为2,3,
由韦达定理可知:,结合,
解得,所以,
所以选项A、B正确;
因为,所以选项C正确;
因为,所以选项D错误.
故选:ABC
18.或
【分析】化简原不等式为,即得解.
【详解】因为,
所以,
即,
所以或.
所以不等式的解集为或.
故答案为:或
19.或
【分析】判断的大小,即可求解不等式的解集.
【详解】∵,∴,
由得或,
故不等式的解集是或,
故答案为:或
20.
【分析】由题得,计算即得解.
【详解】一元二次不等式的解集是,
则和是一元二次方程的实数根,
∴, 解得.
故答案为:
21.
【分析】对不等式的类型分类讨论,根据判别式及二次项系数的符号列式可求出结果.
【详解】①当,即时,
,解得.
②当,即时,
若,则原不等式为,恒成立.
若,则原不等式为,即,不符合题目要求,舍去.
综上所述,当时,原不等式的解集为R.
故答案为:.
22.
【分析】根据题意列式,解不等式可得结果.
【详解】设按销售收入的征收木材税时,税金收入为万元,
则,
令,即,解得.
故答案为:
23.答案见解析
【分析】对不等式变形为,然后对进行合理分类讨论即可.
【详解】原不等式变为,
①当时,原不等式可化为,
所以当时,解得;
当时,解集为;
当时,解得
②当时,原不等式等价于,即.
③当时,,原不等式可化为,
解得或.
综上,当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为,
当时,不等式的解集为或.
24.
【分析】由一元二次不等式的解与二次方程的根之间关系,由韦达定理即可求解.
【详解】由于不等式的解集是,所以和是的两个根,由韦达定理可得且,解得,
25.花卉带宽度的取值范围为(单位:米)
【分析】设花卉带的宽度为米,则草坪的长和宽分别是米,米,由面积关系列不等式,化简后解一元二次不等式得答案.
【详解】设花卉带的宽度为米,则草坪的长和宽分别是米,米,
则,所以,解得
故花卉带宽度的取值范围为(单位:米).
26.
【分析】根据题意,,转化不等式,求解即可.
【详解】解:∵,∴,
原不等式可化为,
解得.
故原不等式的解集为.
27.答案见解析
【分析】分类讨论判别式,确定一元二次不等式对应方程解的情况,即可求得答案.
【详解】不等式对应方程的判别式,
(1)当,即或时,
由于方程的根是,
所以不等式的解集是或};
(2)当,即时,不等式的解集为且;
(3)当,即时,不等式的解集为R,
故或时,不等式的解集是或};
时,不等式的解集为且;
时,不等式的解集为R.
28.
【分析】首先表示出绿草坪的长、宽,即可得到草坪的面积,依题意得到关于的一元二次不等式,解得即可.
【详解】解:花坛的宽度为,所以绿草坪的长为,宽为,
草坪面积为,
总面积,
根据题意可得,
整理得,解得或.
由题意知,解得,所以不符合题意,舍去,
所以.
答:当时,绿草坪的面积不小于总面积的二分之一.
29.当时,不等式解集为,
当时,原不等式的解集为,
当时,原不等式的解集为.
【分析】由二次不等式的解法,注意分类讨论即可.
【详解】因为,所以:①当时,原不等式变为:恒成立,所以此时解集为;
②当时,,则不等式得,
则对应方程的根为:,
当时,原不等式的解集为,
当时,原不等式的解集为.
综上:当时,不等式解集为,
当时,原不等式的解集为,
当时,原不等式的解集为.
30.
【分析】根据二次不等式的解法即得;或参变分离,求函数的最值即得.
【详解】方法一(判别式法)关于x的不等式可变形为,
由题可得,
解得,
又,
所以实数a的取值范围为;
方法二(分离变量法)因为,所以关于x的不等式可变形为,
因为,
所以,解得,
又,所以实数a的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
