专题09 函数的概念及其表示-【夯实基础】2023-2024高一数学同步限时训练(人教A版2019必修第一册)(含解析)
文档属性
| 名称 | 专题09 函数的概念及其表示-【夯实基础】2023-2024高一数学同步限时训练(人教A版2019必修第一册)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 09:20:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【夯实基础】2023-2024高一数学同步限时训练(新人教A版2019)专题09 函数的概念及其表示
一、单选题
1.(2023·全国·高一假期作业)下列变量间为函数关系的是( )
A.匀速行驶的客车在2小时内行驶的路程
B.某地蔬菜的价格与蔬菜的供应量的关系
C.一只60瓦的白炽灯在7小时内的耗电量与时间t的关系
D.生活质量与人的身体状况间的关系
2.(2021秋·河南·高一校考阶段练习)下列图象中,表示函数关系的是( )
A. B. C. D.
3.(2023·全国·高一假期作业)函数的定义域是( )
A. B.
C. D.或
4.(2023·全国·高一假期作业)函数的定义域为( )
A. B. C. D.
5.(2023·全国·高一假期作业)下列各函数中,与函数表示同一函数的是( )
A. B.
C. D.
6.(2023春·高一校考开学考试)已知一次函数满足,则( )
A.12 B.13 C.14 D.15
7.(2023春·安徽·高一合肥市第八中学校联考开学考试)设,则( )
A.6 B.7 C.8 D.9
8.(2021秋·河南平顶山·高一校联考期中)已知函数,则的值域为( )
A. B. C. D.
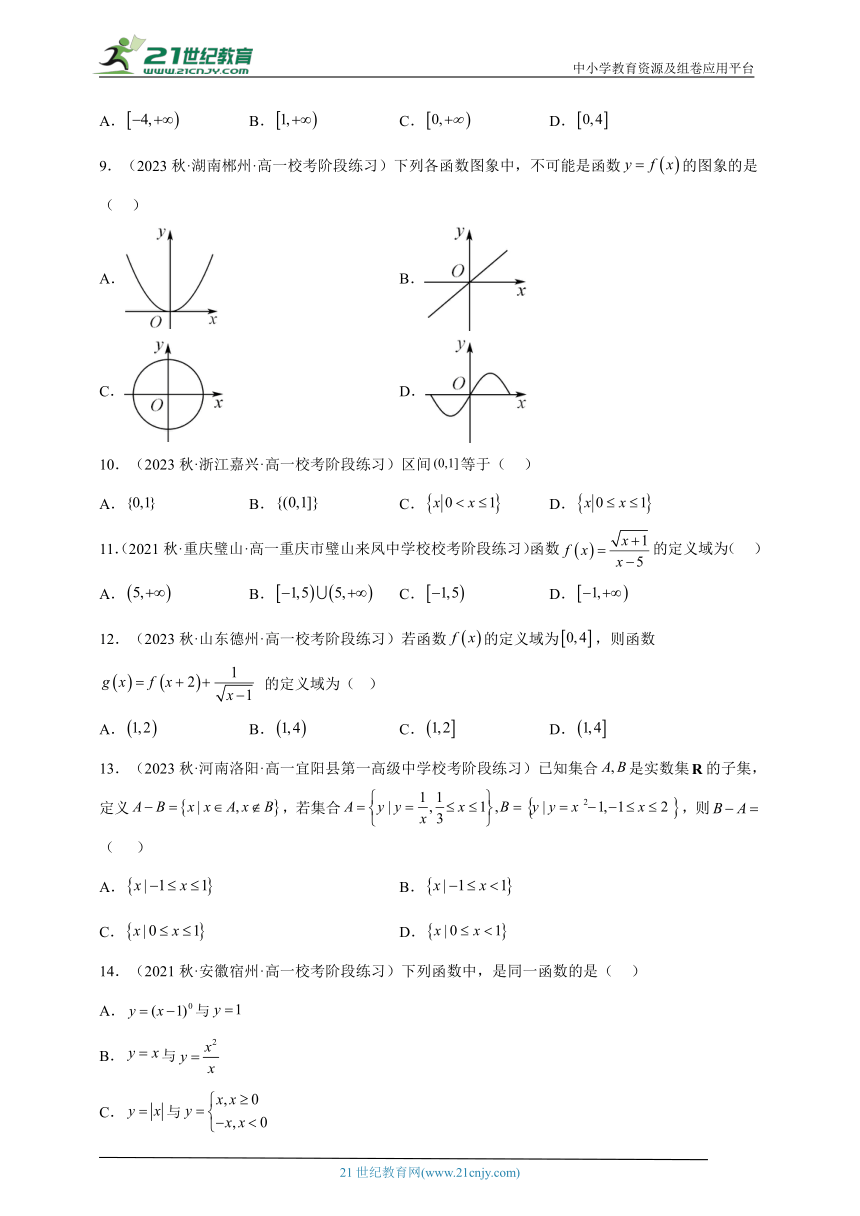
9.(2023秋·湖南郴州·高一校考阶段练习)下列各函数图象中,不可能是函数的图象的是( )
A. B.
C. D.
10.(2023秋·浙江嘉兴·高一校考阶段练习)区间等于( )
A. B. C. D.
11.(2021秋·重庆璧山·高一重庆市璧山来凤中学校校考阶段练习)函数的定义域为( )
A. B. C. D.
12.(2023秋·山东德州·高一校考阶段练习)若函数的定义域为,则函数 的定义域为( )
A. B. C. D.
13.(2023秋·河南洛阳·高一宜阳县第一高级中学校考阶段练习)已知集合是实数集的子集,定义,若集合,则( )
A. B.
C. D.
14.(2021秋·安徽宿州·高一校考阶段练习)下列函数中,是同一函数的是( )
A.与
B.与
C.与
D.与
15.(2023秋·安徽合肥·高一合肥市第六中学校考阶段练习)若函数,且,则实数的值为( )
A.或 B.或3 C. D.3
16.(2023秋·河北保定·高一河北省唐县第一中学校考阶段练习)已知函数的对应关系如下表,则( )
x 0 1 2 3
2 1 3 0
3 2 0
A.0 B.2 C. D.1
17.(2023秋·浙江杭州·高一杭师大附中校考期中)下列各组函数表示相同函数的是( )
A.和 B.和
C.和 D.和
18.(2023春·山东滨州·高一校考阶段练习)函数的定义域是( )
A. B.
C. D.
19.(2023·全国·高一假期作业)已知的定义域为,则的定义域为 ( )
A. B. C. D.
20.(2023·全国·高一假期作业)已知函数的定义域为,则其值域为( )
A. B. C. D.
21.(2023·高一课时练习)下列函数中,值域为的是( )
A. B.
C. D.
22.(2021秋·湖南湘西·高一统考期末)函数,则等于( )
A. B. C. D.
二、多选题
23.(2023·全国·高一假期作业)下列集合不能用区间形式表示的是( )
A. B.
C.或 D.
24.(2023·江苏·高一假期作业)下列各组函数不是同一个函数的是( )
A.与
B.与
C.与
D.与
25.(2023秋·云南昆明·高一云南民族大学附属中学校考阶段练习)下列对应关系中不是到的函数的是( )
A.
B.
C.
D.
26.(2023秋·广东深圳·高一统考期末)下列是函数图象的是( )
A. B.
C. D.
三、填空题
27.(2023·全国·高一假期作业)用区间表示集合__________.
28.(2023秋·浙江衢州·高一校考阶段练习)已知函数,那么________.
29.(2023秋·河北保定·高一校考期中)若函数的定义域是,则它的值域________.
30.(2023春·内蒙古呼和浩特·高一统考阶段练习)若的定义域为,则的定义域为______.
31.(2021秋·吉林松原·高一校考阶段练习)函数的值域为 __________________
32.(2023秋·四川达州·高一校考阶段练习)已知,求_______.
33.(2023·高一课时练习)已知函数的定义域为,则的定义域为______.
34.(2023·高一课时练习)已知,则______.
35.(2023秋·辽宁·高三校联考期中)已知函数,则___________.
36.(2023·全国·高一假期作业)已知函数,分别由下表给出,则______;当时,______.
x 1 2 3
2 1 1
3 2 1
四、解答题
37.(2023·全国·高一假期作业)已知函数的定义域为,求函数的定义域.
38.(2023·全国·高一假期作业)已知的定义域为 ,求的定义域.
39.(2023·全国·高一假期作业)作出下列函数的图象.
(1)y=x+2,|x|≤3;
(2),x∈Z且|x|≤2.
40.(2023·全国·高一假期作业)作出函数的图像.
41.(2023春·内蒙古呼和浩特·高一统考阶段练习)(1)已知,求的解析式;
(2)已知,求的解析式.
42.(2023秋·山东青岛·高一校考阶段练习)(1)已知是一次函数,且满足,求的解析式.
(2)若对任意实数x,均有,求的解析式.
43.(2023秋·广东佛山·高一校考阶段练习)已知函数.
(1)求,的值;
(2)作出函数的简图;
(3)由简图指出函数的值域;
44.(2023·全国·高一假期作业)用区间表示下列集合:
(1);
(2);
(3);
(4);
(5);
(6).
45.(2023·全国·高一假期作业)作出下列函数的图象并求出其值域.
(1),且;
(2),
(3),
46.(2023·高一课时练习)(1)已知函数,求函数的解析式
(2)已知为一次函数,若,求的解析式.
参考答案:
1.C
【分析】根据定义知BD是依赖关系,A是常量,C是确定的函数关系,得到答案.
【详解】对选项A:匀速行驶的客车在2小时内行驶的路程是常量,不满足;
对选项B:某地蔬菜的价格与蔬菜的供应量的关系是依赖关系,不满足;
对选项C:耗电量与时间t的关系是,是确定的函数关系;
对选项D:生活质量与人的身体状况间的关系是依赖关系,不满足.
故选:C
2.D
【分析】利用函数的概念即可求解.
【详解】根据函数的定义知,一个有唯一的对应,由图象可看出,只有选项D的图象满足.
故选:D.
3.A
【分析】根据分式中分母不为0即可求解.
【详解】的自变量需满足,所以定义域为,
故选:A
4.C
【分析】根据函数解析式,可知,解不等式,即可求出结果.
【详解】要使函数有意义,则有,解得且,所以其定义域为.
故选:C.
5.A
【分析】根据函数的定义域以及解析式结合选项逐一判断.
【详解】,故的定义域为,
对于A,的定义域为,且解析式与相同,故为同一个函数,
对于B,,故不是同一个函数,
对于C,的定义域为,而对定义域为,定义域不同,不是同一个函数,
对于D,的定义域为,而对定义域为,定义域不同,不是同一个函数,
故选:A
6.B
【分析】根据待定系数法可得函数解析式,进而即得.
【详解】设,则,
因为,
所以,解得,
所以,.
故选:B.
7.C
【分析】直接利用分段函数的解析式逐步求解函数值即可.
【详解】由,可知.
故选:C.
8.B
【分析】将函数整理成,然后利用二次函数的性质即可求解
【详解】,,
故,故函数值域为.
故选:B
9.C
【分析】根据函数的定义逐项判断,可得出合适的选项.
【详解】对于ABD选项,对于每个都有唯一对应的与之对应,ABD选项中的图象均为函数的图象;
对于C选项,存在,使得这个有两个与之对应,C选项中的图象不是函数的图象.
故选:C.
10.C
【分析】根据区间与集合的概念判断.
【详解】区间表示由的实数组成的集合.
故选:C
11.B
【分析】由解析式有意义列不等式可求函数的定义域.
【详解】由由意义可得,,
所以且,
所以函数的定义域为,
故选:B.
12.C
【分析】根据题意可得出关于的不等式组,由此可解得函数的定义域.
【详解】解:因为函数的定义域为,
对于函数,则,解得,
即函数的定义域为.
故选:C
13.B
【分析】由函数的值域求得,由此求得.
【详解】由题知,
在上递减,所以,
的对称轴为轴,因为,所以,
所以,
故选:B.
14.C
【分析】根据函数的定义判断.
【详解】选项A中,函数的定义域是,函数的定义域是,不是同一函数;
选项B 中,函数的定义域是,函数的定义域是,不是同一函数;
选项C中,两个函数定义域都是,对应法则也相同,是同一函数;
选项D中,两者对应法则不相同,前者对应自变量直接平方,后者对应自变量减去1后的平方,不是同一函数.
故选:C.
15.B
【分析】令,利用配凑法求函数,进而根据求解即可.
【详解】令,则,
可得:,即,
∵,
∴.
故选:B.
16.B
【分析】根据复合函数求值的方法分步求解即可.
【详解】解:,
.
故选:B.
17.C
【分析】根据函数的定义域及对应法则判断是否为同一函数即可.
【详解】对于A中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数;
对于B中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数;
对于C中,函数与的定义域和对应法则都相同,所以表示相同的函数;
对于D中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数.
故选:C
18.D
【分析】列出使函数解析式有意义的不等式,解出的取值范围即函数的定义域.
【详解】由题,,解得.
故选: D.
19.C
【分析】由求出的范围,然后可得答案.
【详解】因为的定义域为,所以,所以,所以的定义域为.
故选:C
20.A
【分析】根据定义域,代入解析式,求出值域.
【详解】当时,,当时,,
故值域为.
故选:A
21.B
【分析】依次判断各个选项中函数的值域即可得到结果.
【详解】对于A,,则其值域为,A错误;
对于B,,则其值域为,B正确;
对于C,,则其值域为,C错误;
对于D,,则其值域为,D错误.
故选:B.
22.D
【分析】利用函数的解析式由内到外逐层计算可得的值.
【详解】因为,则,故.
故选:D.
23.ABD
【分析】根据区间的概念及区间形式可以表示连续数集,是无限集,逐个判断即可得出答案.
【详解】区间形式可以表示连续数集,是无限集
A,D是自然数集的子集,都不能用区间形式表示,
B选项,Q是有理数,数轴上大于1的有理数不是连续的,
故只有C可以,区间形式为,
故选:ABD.
24.ABD
【分析】从定义域和对应法则两方面来判断是否是同一函数.
【详解】对于A,的定义域是,的定义域是R,定义域不同,故不是同一函数,A错;
对于B,与的对应关系不同,故不是同一函数,B错;
对于C,经过化简可知两函数的解析式与定义域都一样,所以为同一函数,C对;
对于D,的定义域是,的定义域是,定义域不同,故不是同一函数,D错.
故选:ABD
25.ACD
【分析】利用函数的概念逐项分析即得.
【详解】A,可化为,显然对任意 (除外),y值不唯一,不符合函数的概念,故A满足题意;
B,符合函数的定义,故B不合题意;
C,,在此时对应关系无意义,不符合函数的定义,故C满足题意;
D,,此时,不符合函数的定义,故D满足题意.
故选:ACD.
26.ABD
【分析】根据函数的定义,进行分析判断即可得解..
【详解】根据函数的定义可知,定义域内的每一个只有一个和它对应,
因此不能出现一对多的情况,所以C不是函数图象,ABD是函数图象.
故选:ABD.
27.
【分析】利用区间的定义得出答案即可.
【详解】集合用区间表示为.
故答案为:
28.
【分析】由分段函数解析式代入求解即可.
【详解】∵,
∴,
∴.
故答案为:.
29..
【分析】由反比例函数的性质求值域.
【详解】∵函数是反比例函数,则时,,且,
所以值域为.
故答案为:.
30.
【分析】根据抽象函数的定义域,结合整体思想即可得解.
【详解】由的定义域为,
令,解得,
所以的定义域为.
故答案为:.
31.
【分析】利用二次函数的单调性求出答案即可.
【详解】因为二次函数的对称轴为,
所以当时
因为当时,时,即,
所以值域为
故答案为:
32.0
【分析】先求出,再求.
【详解】,
.
故答案为:0.
33.
【分析】根据函数性质可知,,计算解出.
【详解】已知函数的定义域为,所以中,
综上定义域为:,取并集解得;
故答案为:
34..
【分析】根据已知把换成,建立方程组求解.
【详解】因为 ①,
把换成有:
②,
联立①②式有:,
解得.
故答案为:.
35.9
【分析】根据函数解析式直接求解即可.
【详解】解:根据题意,
故答案为:9
36. 3 1
【分析】由函数定义计算.
【详解】由表可知,.由表可知,,所以,由表可知,,所以x的值为1.
故答案为:3;1.
37.
【分析】根据抽象函数的定义域求法即可解决
【详解】∵函数的定义域为
∴,解之得:
故函数的定义域为:
38.
【分析】令,,根据二次函数的性质求出的范围,即可得的定义域.
【详解】解:令,,
由二次函数的性质可得,
所以的定义域为.
39.(1)图象见解析
(2)图象见解析
【分析】(1)根据题意,先求出定义域,进而作出函数的图象;
(2)根据题意,先求出定义域,进而作出函数的图象.
【详解】(1)由题意,,函数的图象如图所示:
(2)由题意,,函数的图象如图所示:
【点睛】
40.答案见解析
【分析】先去绝对值号,再作出分段函数的图像.
【详解】因为
所以函数的图像如图所示:
41.(1);(2)
【分析】(1)应用换元法求函数解析式;
(2)构造方程组并作差求函数解析式.
【详解】(1)令,则,故,
所以;
(2)由题设①,结合②,
3×①②得:,故.
42.(1);(2).
【分析】(1)设,利用待定系数法求解即可;
(2)构造关于方程组求解即可.
【详解】(1)因为是一次函数,所以设,,
又因为,
所以,整理得,
故,解得,
所以.
(2)因为①,
所以②,
由①②得:,
解得:.
43.(1),
(2)函数的简图见解析.
(3)
【分析】(1)直接利用分段函数解析式求解函数值.
(2)根据函数类型及性质作函数简图.
(3)由简图直接看出函数的值域.
【详解】(1)由,
∴, .
(2)简图如图所示:
(3)简图可知函数的值域为
44.(1)
(2)
(3)
(4)
(5)
(6)
【分析】直接把集合写成区间的形式,注意含有等号的用闭区间,不含等号的用开区间.
【详解】(1)
(2)
(3)
(4)
(5)
(6)
45.(1)图象见解析,
(2)图象见解析,
(3)图象见解析,
【分析】根据函数的定义域,列表,描点,连线即可画出各函数的图象,求出值域.
【详解】(1)由已知得的定义域为,列表如下:
0 1 2
1 3 5
其图象是离散的点,如图所示,值域为;
(2)列表如下:
2 3 4 5 …
1 …
当时,其图象是反比例函数图象的一部分,如图所示,观察图象知其值域为.
(3)列表如下:
0 1 2
0 0 3 8
其图象是抛物线在之间的部分,如图所示,观察图象知其值域为.
46.(1);(2)或.
【分析】(1)根据给定关系式,利用配凑法求解作答.
(2)设出函数的解析式,再利用待定系数法求解作答.
【详解】(1)函数,则,
所以函数的解析式是.
(2)因为一次函数,设,
则,而,
于是得,解得或,
所以或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【夯实基础】2023-2024高一数学同步限时训练(新人教A版2019)专题09 函数的概念及其表示
一、单选题
1.(2023·全国·高一假期作业)下列变量间为函数关系的是( )
A.匀速行驶的客车在2小时内行驶的路程
B.某地蔬菜的价格与蔬菜的供应量的关系
C.一只60瓦的白炽灯在7小时内的耗电量与时间t的关系
D.生活质量与人的身体状况间的关系
2.(2021秋·河南·高一校考阶段练习)下列图象中,表示函数关系的是( )
A. B. C. D.
3.(2023·全国·高一假期作业)函数的定义域是( )
A. B.
C. D.或
4.(2023·全国·高一假期作业)函数的定义域为( )
A. B. C. D.
5.(2023·全国·高一假期作业)下列各函数中,与函数表示同一函数的是( )
A. B.
C. D.
6.(2023春·高一校考开学考试)已知一次函数满足,则( )
A.12 B.13 C.14 D.15
7.(2023春·安徽·高一合肥市第八中学校联考开学考试)设,则( )
A.6 B.7 C.8 D.9
8.(2021秋·河南平顶山·高一校联考期中)已知函数,则的值域为( )
A. B. C. D.
9.(2023秋·湖南郴州·高一校考阶段练习)下列各函数图象中,不可能是函数的图象的是( )
A. B.
C. D.
10.(2023秋·浙江嘉兴·高一校考阶段练习)区间等于( )
A. B. C. D.
11.(2021秋·重庆璧山·高一重庆市璧山来凤中学校校考阶段练习)函数的定义域为( )
A. B. C. D.
12.(2023秋·山东德州·高一校考阶段练习)若函数的定义域为,则函数 的定义域为( )
A. B. C. D.
13.(2023秋·河南洛阳·高一宜阳县第一高级中学校考阶段练习)已知集合是实数集的子集,定义,若集合,则( )
A. B.
C. D.
14.(2021秋·安徽宿州·高一校考阶段练习)下列函数中,是同一函数的是( )
A.与
B.与
C.与
D.与
15.(2023秋·安徽合肥·高一合肥市第六中学校考阶段练习)若函数,且,则实数的值为( )
A.或 B.或3 C. D.3
16.(2023秋·河北保定·高一河北省唐县第一中学校考阶段练习)已知函数的对应关系如下表,则( )
x 0 1 2 3
2 1 3 0
3 2 0
A.0 B.2 C. D.1
17.(2023秋·浙江杭州·高一杭师大附中校考期中)下列各组函数表示相同函数的是( )
A.和 B.和
C.和 D.和
18.(2023春·山东滨州·高一校考阶段练习)函数的定义域是( )
A. B.
C. D.
19.(2023·全国·高一假期作业)已知的定义域为,则的定义域为 ( )
A. B. C. D.
20.(2023·全国·高一假期作业)已知函数的定义域为,则其值域为( )
A. B. C. D.
21.(2023·高一课时练习)下列函数中,值域为的是( )
A. B.
C. D.
22.(2021秋·湖南湘西·高一统考期末)函数,则等于( )
A. B. C. D.
二、多选题
23.(2023·全国·高一假期作业)下列集合不能用区间形式表示的是( )
A. B.
C.或 D.
24.(2023·江苏·高一假期作业)下列各组函数不是同一个函数的是( )
A.与
B.与
C.与
D.与
25.(2023秋·云南昆明·高一云南民族大学附属中学校考阶段练习)下列对应关系中不是到的函数的是( )
A.
B.
C.
D.
26.(2023秋·广东深圳·高一统考期末)下列是函数图象的是( )
A. B.
C. D.
三、填空题
27.(2023·全国·高一假期作业)用区间表示集合__________.
28.(2023秋·浙江衢州·高一校考阶段练习)已知函数,那么________.
29.(2023秋·河北保定·高一校考期中)若函数的定义域是,则它的值域________.
30.(2023春·内蒙古呼和浩特·高一统考阶段练习)若的定义域为,则的定义域为______.
31.(2021秋·吉林松原·高一校考阶段练习)函数的值域为 __________________
32.(2023秋·四川达州·高一校考阶段练习)已知,求_______.
33.(2023·高一课时练习)已知函数的定义域为,则的定义域为______.
34.(2023·高一课时练习)已知,则______.
35.(2023秋·辽宁·高三校联考期中)已知函数,则___________.
36.(2023·全国·高一假期作业)已知函数,分别由下表给出,则______;当时,______.
x 1 2 3
2 1 1
3 2 1
四、解答题
37.(2023·全国·高一假期作业)已知函数的定义域为,求函数的定义域.
38.(2023·全国·高一假期作业)已知的定义域为 ,求的定义域.
39.(2023·全国·高一假期作业)作出下列函数的图象.
(1)y=x+2,|x|≤3;
(2),x∈Z且|x|≤2.
40.(2023·全国·高一假期作业)作出函数的图像.
41.(2023春·内蒙古呼和浩特·高一统考阶段练习)(1)已知,求的解析式;
(2)已知,求的解析式.
42.(2023秋·山东青岛·高一校考阶段练习)(1)已知是一次函数,且满足,求的解析式.
(2)若对任意实数x,均有,求的解析式.
43.(2023秋·广东佛山·高一校考阶段练习)已知函数.
(1)求,的值;
(2)作出函数的简图;
(3)由简图指出函数的值域;
44.(2023·全国·高一假期作业)用区间表示下列集合:
(1);
(2);
(3);
(4);
(5);
(6).
45.(2023·全国·高一假期作业)作出下列函数的图象并求出其值域.
(1),且;
(2),
(3),
46.(2023·高一课时练习)(1)已知函数,求函数的解析式
(2)已知为一次函数,若,求的解析式.
参考答案:
1.C
【分析】根据定义知BD是依赖关系,A是常量,C是确定的函数关系,得到答案.
【详解】对选项A:匀速行驶的客车在2小时内行驶的路程是常量,不满足;
对选项B:某地蔬菜的价格与蔬菜的供应量的关系是依赖关系,不满足;
对选项C:耗电量与时间t的关系是,是确定的函数关系;
对选项D:生活质量与人的身体状况间的关系是依赖关系,不满足.
故选:C
2.D
【分析】利用函数的概念即可求解.
【详解】根据函数的定义知,一个有唯一的对应,由图象可看出,只有选项D的图象满足.
故选:D.
3.A
【分析】根据分式中分母不为0即可求解.
【详解】的自变量需满足,所以定义域为,
故选:A
4.C
【分析】根据函数解析式,可知,解不等式,即可求出结果.
【详解】要使函数有意义,则有,解得且,所以其定义域为.
故选:C.
5.A
【分析】根据函数的定义域以及解析式结合选项逐一判断.
【详解】,故的定义域为,
对于A,的定义域为,且解析式与相同,故为同一个函数,
对于B,,故不是同一个函数,
对于C,的定义域为,而对定义域为,定义域不同,不是同一个函数,
对于D,的定义域为,而对定义域为,定义域不同,不是同一个函数,
故选:A
6.B
【分析】根据待定系数法可得函数解析式,进而即得.
【详解】设,则,
因为,
所以,解得,
所以,.
故选:B.
7.C
【分析】直接利用分段函数的解析式逐步求解函数值即可.
【详解】由,可知.
故选:C.
8.B
【分析】将函数整理成,然后利用二次函数的性质即可求解
【详解】,,
故,故函数值域为.
故选:B
9.C
【分析】根据函数的定义逐项判断,可得出合适的选项.
【详解】对于ABD选项,对于每个都有唯一对应的与之对应,ABD选项中的图象均为函数的图象;
对于C选项,存在,使得这个有两个与之对应,C选项中的图象不是函数的图象.
故选:C.
10.C
【分析】根据区间与集合的概念判断.
【详解】区间表示由的实数组成的集合.
故选:C
11.B
【分析】由解析式有意义列不等式可求函数的定义域.
【详解】由由意义可得,,
所以且,
所以函数的定义域为,
故选:B.
12.C
【分析】根据题意可得出关于的不等式组,由此可解得函数的定义域.
【详解】解:因为函数的定义域为,
对于函数,则,解得,
即函数的定义域为.
故选:C
13.B
【分析】由函数的值域求得,由此求得.
【详解】由题知,
在上递减,所以,
的对称轴为轴,因为,所以,
所以,
故选:B.
14.C
【分析】根据函数的定义判断.
【详解】选项A中,函数的定义域是,函数的定义域是,不是同一函数;
选项B 中,函数的定义域是,函数的定义域是,不是同一函数;
选项C中,两个函数定义域都是,对应法则也相同,是同一函数;
选项D中,两者对应法则不相同,前者对应自变量直接平方,后者对应自变量减去1后的平方,不是同一函数.
故选:C.
15.B
【分析】令,利用配凑法求函数,进而根据求解即可.
【详解】令,则,
可得:,即,
∵,
∴.
故选:B.
16.B
【分析】根据复合函数求值的方法分步求解即可.
【详解】解:,
.
故选:B.
17.C
【分析】根据函数的定义域及对应法则判断是否为同一函数即可.
【详解】对于A中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数;
对于B中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数;
对于C中,函数与的定义域和对应法则都相同,所以表示相同的函数;
对于D中,函数的定义域为,函数的定义域为,两个函数的定义域不同,所以表示不同的函数.
故选:C
18.D
【分析】列出使函数解析式有意义的不等式,解出的取值范围即函数的定义域.
【详解】由题,,解得.
故选: D.
19.C
【分析】由求出的范围,然后可得答案.
【详解】因为的定义域为,所以,所以,所以的定义域为.
故选:C
20.A
【分析】根据定义域,代入解析式,求出值域.
【详解】当时,,当时,,
故值域为.
故选:A
21.B
【分析】依次判断各个选项中函数的值域即可得到结果.
【详解】对于A,,则其值域为,A错误;
对于B,,则其值域为,B正确;
对于C,,则其值域为,C错误;
对于D,,则其值域为,D错误.
故选:B.
22.D
【分析】利用函数的解析式由内到外逐层计算可得的值.
【详解】因为,则,故.
故选:D.
23.ABD
【分析】根据区间的概念及区间形式可以表示连续数集,是无限集,逐个判断即可得出答案.
【详解】区间形式可以表示连续数集,是无限集
A,D是自然数集的子集,都不能用区间形式表示,
B选项,Q是有理数,数轴上大于1的有理数不是连续的,
故只有C可以,区间形式为,
故选:ABD.
24.ABD
【分析】从定义域和对应法则两方面来判断是否是同一函数.
【详解】对于A,的定义域是,的定义域是R,定义域不同,故不是同一函数,A错;
对于B,与的对应关系不同,故不是同一函数,B错;
对于C,经过化简可知两函数的解析式与定义域都一样,所以为同一函数,C对;
对于D,的定义域是,的定义域是,定义域不同,故不是同一函数,D错.
故选:ABD
25.ACD
【分析】利用函数的概念逐项分析即得.
【详解】A,可化为,显然对任意 (除外),y值不唯一,不符合函数的概念,故A满足题意;
B,符合函数的定义,故B不合题意;
C,,在此时对应关系无意义,不符合函数的定义,故C满足题意;
D,,此时,不符合函数的定义,故D满足题意.
故选:ACD.
26.ABD
【分析】根据函数的定义,进行分析判断即可得解..
【详解】根据函数的定义可知,定义域内的每一个只有一个和它对应,
因此不能出现一对多的情况,所以C不是函数图象,ABD是函数图象.
故选:ABD.
27.
【分析】利用区间的定义得出答案即可.
【详解】集合用区间表示为.
故答案为:
28.
【分析】由分段函数解析式代入求解即可.
【详解】∵,
∴,
∴.
故答案为:.
29..
【分析】由反比例函数的性质求值域.
【详解】∵函数是反比例函数,则时,,且,
所以值域为.
故答案为:.
30.
【分析】根据抽象函数的定义域,结合整体思想即可得解.
【详解】由的定义域为,
令,解得,
所以的定义域为.
故答案为:.
31.
【分析】利用二次函数的单调性求出答案即可.
【详解】因为二次函数的对称轴为,
所以当时
因为当时,时,即,
所以值域为
故答案为:
32.0
【分析】先求出,再求.
【详解】,
.
故答案为:0.
33.
【分析】根据函数性质可知,,计算解出.
【详解】已知函数的定义域为,所以中,
综上定义域为:,取并集解得;
故答案为:
34..
【分析】根据已知把换成,建立方程组求解.
【详解】因为 ①,
把换成有:
②,
联立①②式有:,
解得.
故答案为:.
35.9
【分析】根据函数解析式直接求解即可.
【详解】解:根据题意,
故答案为:9
36. 3 1
【分析】由函数定义计算.
【详解】由表可知,.由表可知,,所以,由表可知,,所以x的值为1.
故答案为:3;1.
37.
【分析】根据抽象函数的定义域求法即可解决
【详解】∵函数的定义域为
∴,解之得:
故函数的定义域为:
38.
【分析】令,,根据二次函数的性质求出的范围,即可得的定义域.
【详解】解:令,,
由二次函数的性质可得,
所以的定义域为.
39.(1)图象见解析
(2)图象见解析
【分析】(1)根据题意,先求出定义域,进而作出函数的图象;
(2)根据题意,先求出定义域,进而作出函数的图象.
【详解】(1)由题意,,函数的图象如图所示:
(2)由题意,,函数的图象如图所示:
【点睛】
40.答案见解析
【分析】先去绝对值号,再作出分段函数的图像.
【详解】因为
所以函数的图像如图所示:
41.(1);(2)
【分析】(1)应用换元法求函数解析式;
(2)构造方程组并作差求函数解析式.
【详解】(1)令,则,故,
所以;
(2)由题设①,结合②,
3×①②得:,故.
42.(1);(2).
【分析】(1)设,利用待定系数法求解即可;
(2)构造关于方程组求解即可.
【详解】(1)因为是一次函数,所以设,,
又因为,
所以,整理得,
故,解得,
所以.
(2)因为①,
所以②,
由①②得:,
解得:.
43.(1),
(2)函数的简图见解析.
(3)
【分析】(1)直接利用分段函数解析式求解函数值.
(2)根据函数类型及性质作函数简图.
(3)由简图直接看出函数的值域.
【详解】(1)由,
∴, .
(2)简图如图所示:
(3)简图可知函数的值域为
44.(1)
(2)
(3)
(4)
(5)
(6)
【分析】直接把集合写成区间的形式,注意含有等号的用闭区间,不含等号的用开区间.
【详解】(1)
(2)
(3)
(4)
(5)
(6)
45.(1)图象见解析,
(2)图象见解析,
(3)图象见解析,
【分析】根据函数的定义域,列表,描点,连线即可画出各函数的图象,求出值域.
【详解】(1)由已知得的定义域为,列表如下:
0 1 2
1 3 5
其图象是离散的点,如图所示,值域为;
(2)列表如下:
2 3 4 5 …
1 …
当时,其图象是反比例函数图象的一部分,如图所示,观察图象知其值域为.
(3)列表如下:
0 1 2
0 0 3 8
其图象是抛物线在之间的部分,如图所示,观察图象知其值域为.
46.(1);(2)或.
【分析】(1)根据给定关系式,利用配凑法求解作答.
(2)设出函数的解析式,再利用待定系数法求解作答.
【详解】(1)函数,则,
所以函数的解析式是.
(2)因为一次函数,设,
则,而,
于是得,解得或,
所以或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
