第04讲 一元一次方程[下学期]
文档属性
| 名称 | 第04讲 一元一次方程[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-08 14:06:00 | ||
图片预览



文档简介
第四讲 一元一次方程
方程是中学数学中最重要的内容.最简单的方程是一元一次方程,它是进一步学习代数方程的基础,很多方程都可以通过变形化为一元一次方程来解决.本讲主要介绍一些解一元一次方程的基本方法和技巧.
用等号连结两个代数式的式子叫等式.如果给等式中的文字代以任何数值,等式都成立,这种等式叫恒等式.一个等式是否是恒等式是要通过证明来确定的.
如果给等式中的文字(未知数)代以某些值,等式成立,而代以其他的值,则等式不成立,这种等式叫作条件等式.条件等式也称为方程.使方程成立的未知数的值叫作方程的解.方程的解的集合,叫作方程的解集.解方程就是求出方程的解集.
只含有一个未知数(又称为一元),且其次数是1的方程叫作一元一次方程.任何一个一元一次方程总可以化为ax=b(a≠0)的形式,这是一元一次方程的标准形式(最简形式).
解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项,化为最简形式ax=b;(5)方程两边同除以未知数的系数,得出方程的解.
一元一次方程ax=b的解由a,b的取值来确定:
(2)若a=0,且b=0,方程变为0·x=0,则方程有无数多个解;
(3)若a=0,且b≠0,方程变为0·x=b,则方程无解.
例1 解方程
解法1 从里到外逐级去括号.去小括号得
去中括号得
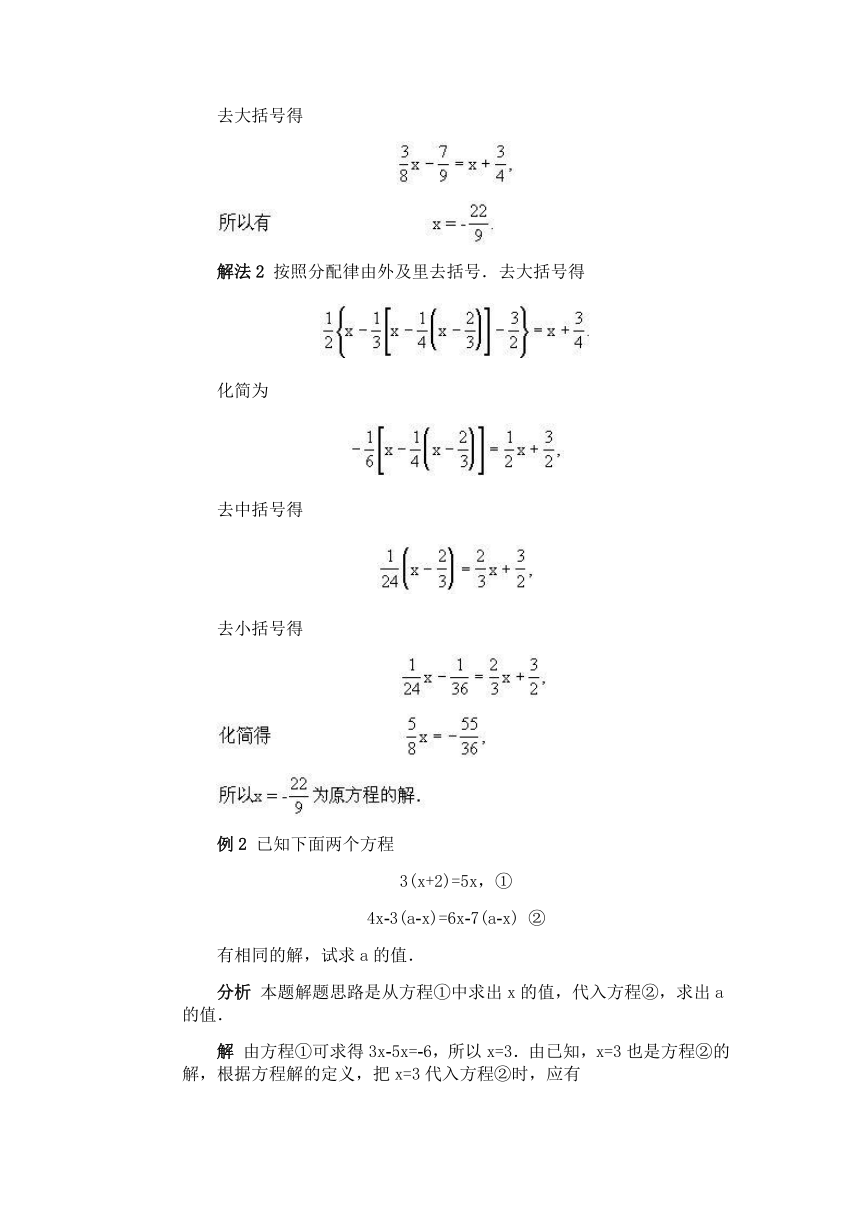
去大括号得
解法2 按照分配律由外及里去括号.去大括号得
化简为
去中括号得
去小括号得
例2 已知下面两个方程
3(x+2)=5x,①
4x-3(a-x)=6x-7(a-x) ②
有相同的解,试求a的值.
分析 本题解题思路是从方程①中求出x的值,代入方程②,求出a的值.
解 由方程①可求得3x-5x=-6,所以x=3.由已知,x=3也是方程②的解,根据方程解的定义,把x=3代入方程②时,应有
4×3-3(a-3)=6×3-7(a-3),
7(a-3)-3(a-3)=18-12,
例3 已知方程2(x+1)=3(x-1)的解为a+2,求方程2[2(x+3)-3(x-a)]=3a的解.
解 由方程2(x+1)=3(x-1)解得x=5.由题设知a+2=5,所以a=3.于是有
2[2(x+3)-3(x-3)]=3×3,-2x=-21,
例4 解关于x的方程(mx-n)(m+n)=0.
分析 这个方程中未知数是x,m,n是可以取不同实数值的常数,因此需要讨论m,n取不同值时,方程解的情况.
解 把原方程化为
m2x+mnx-mn-n2=0,
整理得 m(m+n)x=n(m+n).
当m+n≠0,且m=0时,方程无解;
当m+n=0时,方程的解为一切实数.
说明 含有字母系数的方程,一定要注意字母的取值范围.解这类方程时,需要从方程有唯一解、无解、无数多个解三种情况进行讨论.
例5 解方程
(a+x-b)(a-b-x)=(a2-x)(b2+x)-a2b2.
分析 本题将方程中的括号去掉后产生x2项,但整理化简后,可以消去x2,也就是说,原方程实际上仍是一个一元一次方程.
解 将原方程整理化简得
(a-b)2-x2=a2b2+a2x-b2x-x2-a2b2,
即 (a2-b2)x=(a-b)2.
(1)当a2-b2≠0时,即a≠±b时,方程有唯一解
(2)当a2-b2=0时,即a=b或a=-b时,若a-b≠0,即a≠b,即a=-b时,方程无解;若a-b=0,即a=b,方程有无数多个解.
例6 已知(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,求代数式199(m+x)(x-2m)+m的值.
解 因为(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,所以
m2-1=0,即m=±1.
(1)当m=1时,方程变为-2x+8=0,因此x=4,代数式的值为
199(1+4)(4-2×1)+1=1991;
(2)当m=-1时,原方程无解.
所以所求代数式的值为1991.
例7 已知关于x的方程a(2x-1)=3x-2无解,试求a的值.
解 将原方程变形为
2ax-a=3x-2,
即 (2a-3)x=a-2.
由已知该方程无解,所以
例8 k为何正数时,方程k2x-k2=2kx-5k的解是正数?
来确定:
(1)若b=0时,方程的解是零;反之,若方程ax=b的解是零,则b=0成立.
(2)若ab>0时,则方程的解是正数;反之,若方程ax=b的解是正数,则ab>0成立.
(3)若ab<0时,则方程的解是负数;反之,若方程ax=b的解是负数,则ab<0成立.
解 按未知数x整理方程得
(k2-2k)x=k2-5k.
要使方程的解为正数,需要
(k2-2k)(k2-5k)>0.
看不等式的左端
(k2-2k)(k2-5k)=k2(k-2)(k-5).
因为k2≥0,所以只要k>5或k<2时上式大于零,所以当k<2或k>5时,原方程的解是正数,所以k>5或0<k<2即为所求.
例9 若abc=1,解方程
解 因为abc=1,所以原方程可变形为
化简整理为
化简整理为
说明 像这种带有附加条件的方程,求解时恰当地利用附加条件可使方程的求解过程大大简化.
例10 若a,b,c是正数,解方程
解法1 原方程两边乘以abc,得到方程
ab(x-a-b)+bc(x-b-c)+ac(x-c-a)=3abc.移项、合并同类项得
ab[x-(a+b+c)]+bc[x-(a+b+c)]
+ac[x-(a+b+c)]=0,
因此有
[x-(a+b+c)](ab+bc+ac)=0.
因为a>0,b>0,c>0,所以ab+bc+ac≠0,所以
x-(a+b+c)=0,
即x=a+b+c为原方程的解.
解法2 将原方程右边的3移到左边变为-3,再拆为三个“-1”,并注意到
其余两项做类似处理.
设m=a+b+c,则原方程变形为
所以
即
x-(a+b+c)=0.
所以x=a+b+c为原方程的解.
说明 注意观察,巧妙变形,是产生简单优美解法所不可缺少的基本功之一.
例11 设n为自然数,[x]表示不超过x的最大整数,解方程:
分析 要解此方程,必须先去掉[ ],由于n是自然数,所以n与(n+1)
…,n[x]都是整数,所以x必是整数.
解 根据分析,x必为整数,即x=[x],所以原方程化为
合并同类项得
故有
所以x=n(n+1)为原方程的解.
例12 已知关于x的方程
且a为某些自然数时,方程的解为自然数,试求自然数a的最小值.
解 由原方程可解得
a最小,所以x应取x=160.所以
所以满足题设的自然数a的最小值为2.
练习四
1.解下列方程:*
2.解下列关于x的方程:
(1)a2(x-2)-3a=x+1;
4.当k取何值时,关于x的方程3(x+1)=5-kx,分别有:(1)正数解;(2)负数解;(3)不大于1的解.
方程是中学数学中最重要的内容.最简单的方程是一元一次方程,它是进一步学习代数方程的基础,很多方程都可以通过变形化为一元一次方程来解决.本讲主要介绍一些解一元一次方程的基本方法和技巧.
用等号连结两个代数式的式子叫等式.如果给等式中的文字代以任何数值,等式都成立,这种等式叫恒等式.一个等式是否是恒等式是要通过证明来确定的.
如果给等式中的文字(未知数)代以某些值,等式成立,而代以其他的值,则等式不成立,这种等式叫作条件等式.条件等式也称为方程.使方程成立的未知数的值叫作方程的解.方程的解的集合,叫作方程的解集.解方程就是求出方程的解集.
只含有一个未知数(又称为一元),且其次数是1的方程叫作一元一次方程.任何一个一元一次方程总可以化为ax=b(a≠0)的形式,这是一元一次方程的标准形式(最简形式).
解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项,化为最简形式ax=b;(5)方程两边同除以未知数的系数,得出方程的解.
一元一次方程ax=b的解由a,b的取值来确定:
(2)若a=0,且b=0,方程变为0·x=0,则方程有无数多个解;
(3)若a=0,且b≠0,方程变为0·x=b,则方程无解.
例1 解方程
解法1 从里到外逐级去括号.去小括号得
去中括号得
去大括号得
解法2 按照分配律由外及里去括号.去大括号得
化简为
去中括号得
去小括号得
例2 已知下面两个方程
3(x+2)=5x,①
4x-3(a-x)=6x-7(a-x) ②
有相同的解,试求a的值.
分析 本题解题思路是从方程①中求出x的值,代入方程②,求出a的值.
解 由方程①可求得3x-5x=-6,所以x=3.由已知,x=3也是方程②的解,根据方程解的定义,把x=3代入方程②时,应有
4×3-3(a-3)=6×3-7(a-3),
7(a-3)-3(a-3)=18-12,
例3 已知方程2(x+1)=3(x-1)的解为a+2,求方程2[2(x+3)-3(x-a)]=3a的解.
解 由方程2(x+1)=3(x-1)解得x=5.由题设知a+2=5,所以a=3.于是有
2[2(x+3)-3(x-3)]=3×3,-2x=-21,
例4 解关于x的方程(mx-n)(m+n)=0.
分析 这个方程中未知数是x,m,n是可以取不同实数值的常数,因此需要讨论m,n取不同值时,方程解的情况.
解 把原方程化为
m2x+mnx-mn-n2=0,
整理得 m(m+n)x=n(m+n).
当m+n≠0,且m=0时,方程无解;
当m+n=0时,方程的解为一切实数.
说明 含有字母系数的方程,一定要注意字母的取值范围.解这类方程时,需要从方程有唯一解、无解、无数多个解三种情况进行讨论.
例5 解方程
(a+x-b)(a-b-x)=(a2-x)(b2+x)-a2b2.
分析 本题将方程中的括号去掉后产生x2项,但整理化简后,可以消去x2,也就是说,原方程实际上仍是一个一元一次方程.
解 将原方程整理化简得
(a-b)2-x2=a2b2+a2x-b2x-x2-a2b2,
即 (a2-b2)x=(a-b)2.
(1)当a2-b2≠0时,即a≠±b时,方程有唯一解
(2)当a2-b2=0时,即a=b或a=-b时,若a-b≠0,即a≠b,即a=-b时,方程无解;若a-b=0,即a=b,方程有无数多个解.
例6 已知(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,求代数式199(m+x)(x-2m)+m的值.
解 因为(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,所以
m2-1=0,即m=±1.
(1)当m=1时,方程变为-2x+8=0,因此x=4,代数式的值为
199(1+4)(4-2×1)+1=1991;
(2)当m=-1时,原方程无解.
所以所求代数式的值为1991.
例7 已知关于x的方程a(2x-1)=3x-2无解,试求a的值.
解 将原方程变形为
2ax-a=3x-2,
即 (2a-3)x=a-2.
由已知该方程无解,所以
例8 k为何正数时,方程k2x-k2=2kx-5k的解是正数?
来确定:
(1)若b=0时,方程的解是零;反之,若方程ax=b的解是零,则b=0成立.
(2)若ab>0时,则方程的解是正数;反之,若方程ax=b的解是正数,则ab>0成立.
(3)若ab<0时,则方程的解是负数;反之,若方程ax=b的解是负数,则ab<0成立.
解 按未知数x整理方程得
(k2-2k)x=k2-5k.
要使方程的解为正数,需要
(k2-2k)(k2-5k)>0.
看不等式的左端
(k2-2k)(k2-5k)=k2(k-2)(k-5).
因为k2≥0,所以只要k>5或k<2时上式大于零,所以当k<2或k>5时,原方程的解是正数,所以k>5或0<k<2即为所求.
例9 若abc=1,解方程
解 因为abc=1,所以原方程可变形为
化简整理为
化简整理为
说明 像这种带有附加条件的方程,求解时恰当地利用附加条件可使方程的求解过程大大简化.
例10 若a,b,c是正数,解方程
解法1 原方程两边乘以abc,得到方程
ab(x-a-b)+bc(x-b-c)+ac(x-c-a)=3abc.移项、合并同类项得
ab[x-(a+b+c)]+bc[x-(a+b+c)]
+ac[x-(a+b+c)]=0,
因此有
[x-(a+b+c)](ab+bc+ac)=0.
因为a>0,b>0,c>0,所以ab+bc+ac≠0,所以
x-(a+b+c)=0,
即x=a+b+c为原方程的解.
解法2 将原方程右边的3移到左边变为-3,再拆为三个“-1”,并注意到
其余两项做类似处理.
设m=a+b+c,则原方程变形为
所以
即
x-(a+b+c)=0.
所以x=a+b+c为原方程的解.
说明 注意观察,巧妙变形,是产生简单优美解法所不可缺少的基本功之一.
例11 设n为自然数,[x]表示不超过x的最大整数,解方程:
分析 要解此方程,必须先去掉[ ],由于n是自然数,所以n与(n+1)
…,n[x]都是整数,所以x必是整数.
解 根据分析,x必为整数,即x=[x],所以原方程化为
合并同类项得
故有
所以x=n(n+1)为原方程的解.
例12 已知关于x的方程
且a为某些自然数时,方程的解为自然数,试求自然数a的最小值.
解 由原方程可解得
a最小,所以x应取x=160.所以
所以满足题设的自然数a的最小值为2.
练习四
1.解下列方程:*
2.解下列关于x的方程:
(1)a2(x-2)-3a=x+1;
4.当k取何值时,关于x的方程3(x+1)=5-kx,分别有:(1)正数解;(2)负数解;(3)不大于1的解.
