13讲 从三角形内角和谈起[下学期]
文档属性
| 名称 | 13讲 从三角形内角和谈起[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 90.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-06 00:00:00 | ||
图片预览




文档简介
第十三讲 从三角形内角和谈起
三角形的内角和等于180°(也称一个平角)是三角形的一个基本性质.从它出发可引出下面两个事实:
(1)三角形的外角等于此三角形中与它不相邻的两个内角和.
如图1-35所示.延长三角形的三条边,由三角形一条边
及另一条边的延长线所成的角称为该三角形的一个外角.如图1-35中的∠1,∠2,∠3,∠4,∠5,∠6.由于
∠1+∠ABC=180°(平角),
又
∠BAC+∠BCA+∠ABC=180°,
所以
∠1=∠BAC+∠BCA.
同法可证
∠3=∠BAC+∠ABC,
∠5=∠ABC+∠ACB.
(2)n边形的内角和等于(n-2)×180°.
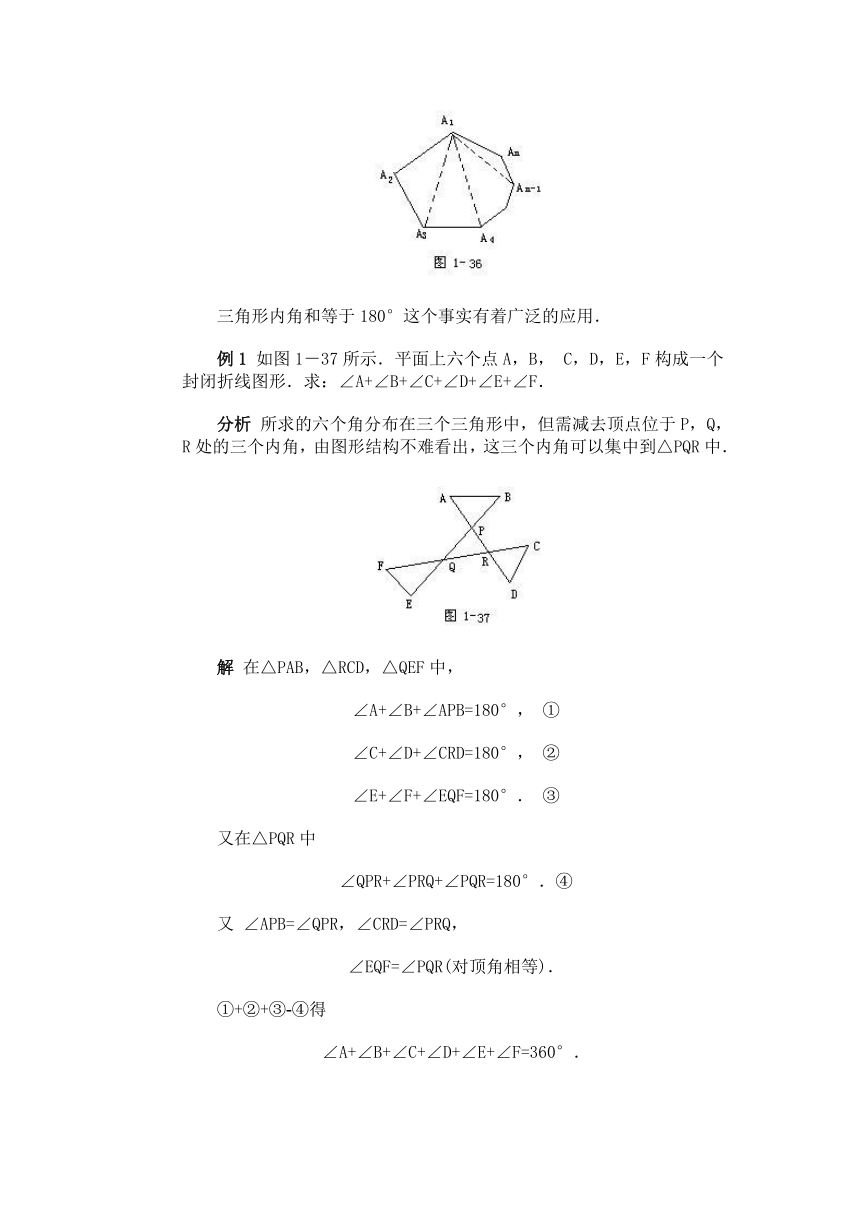
如图1-36所示.以n边形A1A2…An的某一个顶点(如A1)为共同顶点,将这个n边形“分割成” n-2个三角形△A1A2A3,△A1A3A4,…, △A1An-1An.由于每一个三角形的内角和等于180°,所以,这n-2个三角形的内角和(即n边形的内角和)为(n-2)×180°(详证见后面例 6).
三角形内角和等于180°这个事实有着广泛的应用.
例1 如图1-37所示.平面上六个点A,B, C,D,E,F构成一个封闭折线图形.求:∠A+∠B+∠C+∠D+∠E+∠F.
分析 所求的六个角分布在三个三角形中,但需减去顶点位于P,Q,R处的三个内角,由图形结构不难看出,这三个内角可以集中到△PQR中.
解 在△PAB,△RCD,△QEF中,
∠A+∠B+∠APB=180°, ①
∠C+∠D+∠CRD=180°, ②
∠E+∠F+∠EQF=180°. ③
又在△PQR中
∠QPR+∠PRQ+∠PQR=180°.④
又 ∠APB=∠QPR,∠CRD=∠PRQ,
∠EQF=∠PQR(对顶角相等).
①+②+③-④得
∠A+∠B+∠C+∠D+∠E+∠F=360°.
说明 依据图形的特点,利用几何图形的性质将分散的角集中到某些三角形之中,是利用三角形内角和性质的前提.
例2 求如图1-38所示图形中∠A+∠B+∠C+∠D+∠E的大小.
分析 如果我们注意力放在三角形内角和上,那么
∠ABE=∠ABO+∠OBE,
∠AEB=∠AED+∠OEB.
而∠ABE,∠AEB属于△ABE,∠OBE,∠OEB属于△OBE,再注意到△OBE及△ODC中,因∠BOE=∠COD(对顶角),因而, ∠D+∠C=∠OBE+∠OEB.从而,可求出题中五角和.
解法1 连接BE.在△COD中,
∠C+∠D+∠COD=180°. ①
在△ABE中,
∠A+∠ABE+∠AEB=180°. ②
①+②得
(∠A+∠C+∠D)+∠COD+∠ABE+∠AEB=360°. ③
又
∠ABE=∠ABO(即为∠B)+∠OBE,
∠AEB=∠AEO(即为∠E)+∠OEB.
故③式可化为
(∠A+∠B+∠C+∠D+∠E)
+(∠COD+∠OBE+∠OEB)=360°.④
由于
∠COD=∠BOE(对顶角相等),
在△BOE中
∠COD+∠OBE+∠OEB
=∠BOE+∠OBE+∠OEB
=180°.
由④得 ∠A+∠B+∠C+∠D+∠E=180°.
解法2 如果我们注意到三角形外角的性质,结合图形(图1-39)会发现在△OCD中有∠1=∠C+∠D,△APE中∠2=∠A+∠E,在△BOP中∠1+∠2+∠B=180°,从而有∠A+∠B+∠C+∠D+∠E=180°.
说明 本例解法2比解法1简洁,因为我们应用了关于三角形外角的性质.
例3 如图1-40所示.在△ABC中,∠B的平分线与∠C的外角平分线交于D,且∠D=30°.求∠A的度数.
分析∠D位于△BCD中,∠A位于△ABC中,它们位于两个不同的三角形之中,欲利用三角形内角和定理解决问题,就必须寻求两个三角形中内角之间的关系,角平分线的条件为我们提供了信息,事实上∠
解 由已知,∠D=30°.在△BCD中,
∠CBD+∠BCD=180°-30°=150°.①
因为BD是∠ABC的平分线,所以
又因为CD是∠ACE的平分线,所以
从而
由①,②,③
即
所以
所以 ∠A=60°.
说明 解决本题的关键在于两条角平分线架起了△ABC与△BCD之间的桥梁,完成了从已知向未知的过渡.细心审题,发现已知与所求之间的联系,常是解题的重要前提.
例4 如图1-41所示.∠A=10°,∠ABC=90°,
∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.求∠F的度数.
分析 如果我们能注意到所给的一系列等角条件正反映了内角与外角的关系,问题就不难解决.例如在∠ACB=∠DCE中,∠ACB是△ABC的一个内角,∠DCE是△ACD的外角.∠ADC=∠EDF及∠CED=∠FEG两个等式两边的角也是类似情况,这就为我们利用外角定理解题创造了机会.
解 在△ABC中,∠A=10°,∠ABC=90°,所以∠ACB=80°.因为
∠DCE=∠ACB=80°,
在△ACD中,∠DCE是它的一个外角,所以
∠DCE=∠A+∠ADC,
80°=10°+∠ADC,
所以
∠ADC=70°,∠EDF=∠ADC=70°.
在△ADE中,∠EDF是它的一个外角,所以
∠EDF=∠A+∠AED,
70°=10°+∠AED,
所以
∠AED=60°,∠FEG=∠AED=60°.
在△AEF中,∠FEG是它的一个外角,所以
∠FEG=∠A+∠F,
所以
∠F=∠FEG-∠A=60°-10°=50°.
例5 如图1-42所示.△ABC的边BA延长线与外角∠ACE的平分线交于D.求证:∠BAC>∠B.
分析 三角形的外角定理的意义中已暗含着“三角形的外角大于三角形中与此外角不相邻的内角”的意义.证明有关三角形角的不等问题可从此下手.
证 ∠BAC是△ACD的一个外角,因为∠BAC=∠1+∠D,所以2∠BAC=2∠1+2∠D=∠ACE+2∠D>∠ACE①(因为CD是∠ACE的平分线).又∠ACE是△ABC的一个外角,所以
∠ACE=∠B+∠BAC. ②
由②,③
2∠BAC>∠B+∠BAC,
所以 ∠BAC>∠B.
由于多边形可以分割为若干个三角形,因而多边形的内角和可以转化为三角形内角和来计算.下面我们来求n(n≥3的自然数)边形的内角和.
例6 n边形的内角和等于(n-2)·180°.
分析 我们不妨先从具体情况入手.
当n=4时,如图1-43所示.四边形ABCD用一条对角线可以分割成两个三角形,因此
四边形ABCD的内角和=三角形ABC的内角和+三角形ACD的内角和
=2×180°=360°.
当n=5时,如图1-44所示.五边形ABCDE用两条对角线可以分割为三个三角形.类似于n=4的情况,可证明:五边形ABCDE的内角和=3×180°=540°.
由这两个具体实例,我们可以找到n边形的内角和的证明方法.
证 在n边形A1A2A3…An中,以A1为一个端点,连接对角线A1A3,A1A4,…,A1An-1,共有(n-1)-3+1=n-3条对角线,将这个n边形分割成n-2个三角形.显然,这n-2个三角形的内角“合并”起来恰是这个n边形的n个内角,如图1-45所示.所以
n边形的内角和=(n-2)×180°.
说明(1)从具体的简单的问题入手常能找到解决复杂问题的思路.如本题从n=4,5入手,找到将多边形分割为三角形的方法(这是一个本质的方法),从而可以推广到n为任意自然数的范围中去.
(2)各条边都相等,各个内角都相等的多边形称为正多边形.由本例自然可以推出正n边形每一个内角的大小.
设正n边形的一个内角大小为a,则
n边形的内角和=na=(n-2)×180°,
所以
例如正五边形的内角的度数为
正十边形的内角度数为
练习十三
1.如图1-46所示.∠A+∠B+∠C+∠D+∠E的大小.
2.如图 1-47所示.求 ∠A+∠B+∠C+∠D+∠E的大小.
3.如图1-48所示.求∠A+∠B+∠C+∠D+∠E+∠F的大小.
4.如图1-49所示.求∠a+∠B+∠C+∠D+∠E+∠F+∠G的大小.
5.如图1-50所示.△ABC中,AE是∠A的平分线,CD⊥AE于D.求证:∠ACD>∠B.
6.若多边形内角和分别为下列度数时,试分别求出多边形的边数:
(1)1260°;(2)2160°.
7.证明:n边形的外角和等于360°.
三角形的内角和等于180°(也称一个平角)是三角形的一个基本性质.从它出发可引出下面两个事实:
(1)三角形的外角等于此三角形中与它不相邻的两个内角和.
如图1-35所示.延长三角形的三条边,由三角形一条边
及另一条边的延长线所成的角称为该三角形的一个外角.如图1-35中的∠1,∠2,∠3,∠4,∠5,∠6.由于
∠1+∠ABC=180°(平角),
又
∠BAC+∠BCA+∠ABC=180°,
所以
∠1=∠BAC+∠BCA.
同法可证
∠3=∠BAC+∠ABC,
∠5=∠ABC+∠ACB.
(2)n边形的内角和等于(n-2)×180°.
如图1-36所示.以n边形A1A2…An的某一个顶点(如A1)为共同顶点,将这个n边形“分割成” n-2个三角形△A1A2A3,△A1A3A4,…, △A1An-1An.由于每一个三角形的内角和等于180°,所以,这n-2个三角形的内角和(即n边形的内角和)为(n-2)×180°(详证见后面例 6).
三角形内角和等于180°这个事实有着广泛的应用.
例1 如图1-37所示.平面上六个点A,B, C,D,E,F构成一个封闭折线图形.求:∠A+∠B+∠C+∠D+∠E+∠F.
分析 所求的六个角分布在三个三角形中,但需减去顶点位于P,Q,R处的三个内角,由图形结构不难看出,这三个内角可以集中到△PQR中.
解 在△PAB,△RCD,△QEF中,
∠A+∠B+∠APB=180°, ①
∠C+∠D+∠CRD=180°, ②
∠E+∠F+∠EQF=180°. ③
又在△PQR中
∠QPR+∠PRQ+∠PQR=180°.④
又 ∠APB=∠QPR,∠CRD=∠PRQ,
∠EQF=∠PQR(对顶角相等).
①+②+③-④得
∠A+∠B+∠C+∠D+∠E+∠F=360°.
说明 依据图形的特点,利用几何图形的性质将分散的角集中到某些三角形之中,是利用三角形内角和性质的前提.
例2 求如图1-38所示图形中∠A+∠B+∠C+∠D+∠E的大小.
分析 如果我们注意力放在三角形内角和上,那么
∠ABE=∠ABO+∠OBE,
∠AEB=∠AED+∠OEB.
而∠ABE,∠AEB属于△ABE,∠OBE,∠OEB属于△OBE,再注意到△OBE及△ODC中,因∠BOE=∠COD(对顶角),因而, ∠D+∠C=∠OBE+∠OEB.从而,可求出题中五角和.
解法1 连接BE.在△COD中,
∠C+∠D+∠COD=180°. ①
在△ABE中,
∠A+∠ABE+∠AEB=180°. ②
①+②得
(∠A+∠C+∠D)+∠COD+∠ABE+∠AEB=360°. ③
又
∠ABE=∠ABO(即为∠B)+∠OBE,
∠AEB=∠AEO(即为∠E)+∠OEB.
故③式可化为
(∠A+∠B+∠C+∠D+∠E)
+(∠COD+∠OBE+∠OEB)=360°.④
由于
∠COD=∠BOE(对顶角相等),
在△BOE中
∠COD+∠OBE+∠OEB
=∠BOE+∠OBE+∠OEB
=180°.
由④得 ∠A+∠B+∠C+∠D+∠E=180°.
解法2 如果我们注意到三角形外角的性质,结合图形(图1-39)会发现在△OCD中有∠1=∠C+∠D,△APE中∠2=∠A+∠E,在△BOP中∠1+∠2+∠B=180°,从而有∠A+∠B+∠C+∠D+∠E=180°.
说明 本例解法2比解法1简洁,因为我们应用了关于三角形外角的性质.
例3 如图1-40所示.在△ABC中,∠B的平分线与∠C的外角平分线交于D,且∠D=30°.求∠A的度数.
分析∠D位于△BCD中,∠A位于△ABC中,它们位于两个不同的三角形之中,欲利用三角形内角和定理解决问题,就必须寻求两个三角形中内角之间的关系,角平分线的条件为我们提供了信息,事实上∠
解 由已知,∠D=30°.在△BCD中,
∠CBD+∠BCD=180°-30°=150°.①
因为BD是∠ABC的平分线,所以
又因为CD是∠ACE的平分线,所以
从而
由①,②,③
即
所以
所以 ∠A=60°.
说明 解决本题的关键在于两条角平分线架起了△ABC与△BCD之间的桥梁,完成了从已知向未知的过渡.细心审题,发现已知与所求之间的联系,常是解题的重要前提.
例4 如图1-41所示.∠A=10°,∠ABC=90°,
∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.求∠F的度数.
分析 如果我们能注意到所给的一系列等角条件正反映了内角与外角的关系,问题就不难解决.例如在∠ACB=∠DCE中,∠ACB是△ABC的一个内角,∠DCE是△ACD的外角.∠ADC=∠EDF及∠CED=∠FEG两个等式两边的角也是类似情况,这就为我们利用外角定理解题创造了机会.
解 在△ABC中,∠A=10°,∠ABC=90°,所以∠ACB=80°.因为
∠DCE=∠ACB=80°,
在△ACD中,∠DCE是它的一个外角,所以
∠DCE=∠A+∠ADC,
80°=10°+∠ADC,
所以
∠ADC=70°,∠EDF=∠ADC=70°.
在△ADE中,∠EDF是它的一个外角,所以
∠EDF=∠A+∠AED,
70°=10°+∠AED,
所以
∠AED=60°,∠FEG=∠AED=60°.
在△AEF中,∠FEG是它的一个外角,所以
∠FEG=∠A+∠F,
所以
∠F=∠FEG-∠A=60°-10°=50°.
例5 如图1-42所示.△ABC的边BA延长线与外角∠ACE的平分线交于D.求证:∠BAC>∠B.
分析 三角形的外角定理的意义中已暗含着“三角形的外角大于三角形中与此外角不相邻的内角”的意义.证明有关三角形角的不等问题可从此下手.
证 ∠BAC是△ACD的一个外角,因为∠BAC=∠1+∠D,所以2∠BAC=2∠1+2∠D=∠ACE+2∠D>∠ACE①(因为CD是∠ACE的平分线).又∠ACE是△ABC的一个外角,所以
∠ACE=∠B+∠BAC. ②
由②,③
2∠BAC>∠B+∠BAC,
所以 ∠BAC>∠B.
由于多边形可以分割为若干个三角形,因而多边形的内角和可以转化为三角形内角和来计算.下面我们来求n(n≥3的自然数)边形的内角和.
例6 n边形的内角和等于(n-2)·180°.
分析 我们不妨先从具体情况入手.
当n=4时,如图1-43所示.四边形ABCD用一条对角线可以分割成两个三角形,因此
四边形ABCD的内角和=三角形ABC的内角和+三角形ACD的内角和
=2×180°=360°.
当n=5时,如图1-44所示.五边形ABCDE用两条对角线可以分割为三个三角形.类似于n=4的情况,可证明:五边形ABCDE的内角和=3×180°=540°.
由这两个具体实例,我们可以找到n边形的内角和的证明方法.
证 在n边形A1A2A3…An中,以A1为一个端点,连接对角线A1A3,A1A4,…,A1An-1,共有(n-1)-3+1=n-3条对角线,将这个n边形分割成n-2个三角形.显然,这n-2个三角形的内角“合并”起来恰是这个n边形的n个内角,如图1-45所示.所以
n边形的内角和=(n-2)×180°.
说明(1)从具体的简单的问题入手常能找到解决复杂问题的思路.如本题从n=4,5入手,找到将多边形分割为三角形的方法(这是一个本质的方法),从而可以推广到n为任意自然数的范围中去.
(2)各条边都相等,各个内角都相等的多边形称为正多边形.由本例自然可以推出正n边形每一个内角的大小.
设正n边形的一个内角大小为a,则
n边形的内角和=na=(n-2)×180°,
所以
例如正五边形的内角的度数为
正十边形的内角度数为
练习十三
1.如图1-46所示.∠A+∠B+∠C+∠D+∠E的大小.
2.如图 1-47所示.求 ∠A+∠B+∠C+∠D+∠E的大小.
3.如图1-48所示.求∠A+∠B+∠C+∠D+∠E+∠F的大小.
4.如图1-49所示.求∠a+∠B+∠C+∠D+∠E+∠F+∠G的大小.
5.如图1-50所示.△ABC中,AE是∠A的平分线,CD⊥AE于D.求证:∠ACD>∠B.
6.若多边形内角和分别为下列度数时,试分别求出多边形的边数:
(1)1260°;(2)2160°.
7.证明:n边形的外角和等于360°.
