北师大版九年级 数学上 册1.2 矩形的性质与判定课件(42张PPT)
文档属性
| 名称 | 北师大版九年级 数学上 册1.2 矩形的性质与判定课件(42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 15:37:01 | ||
图片预览







文档简介
(共42张PPT)
北师大版 九年级上册数学
第一章 特殊平行四边形
1.2 矩形的性质与判定
观察下面图形,长方形在生活中无处不在.
情景引入
1.2 .1 矩形的性质
思考 长方形跟我们前面学行四边形有什么关系?
你还能举出其他的例子吗?
合作学习
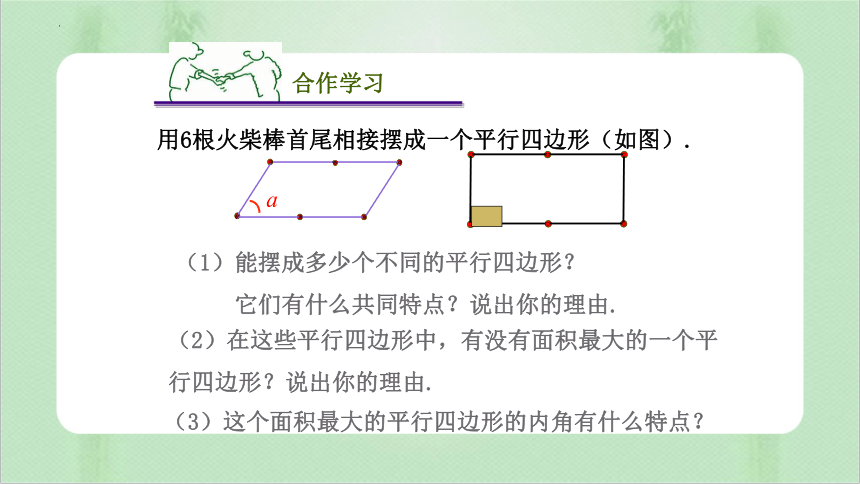
用6根火柴棒首尾相接摆成一个平行四边形(如图).
(1)能摆成多少个不同的平行四边形?
它们有什么共同特点?说出你的理由.
(2)在这些平行四边形中,有没有面积最大的一个平 行四边形?说出你的理由.
(3)这个面积最大的平行四边形的内角有什么特点?
a
α
A D
A D
B C
A D
A D
A
B
C
D
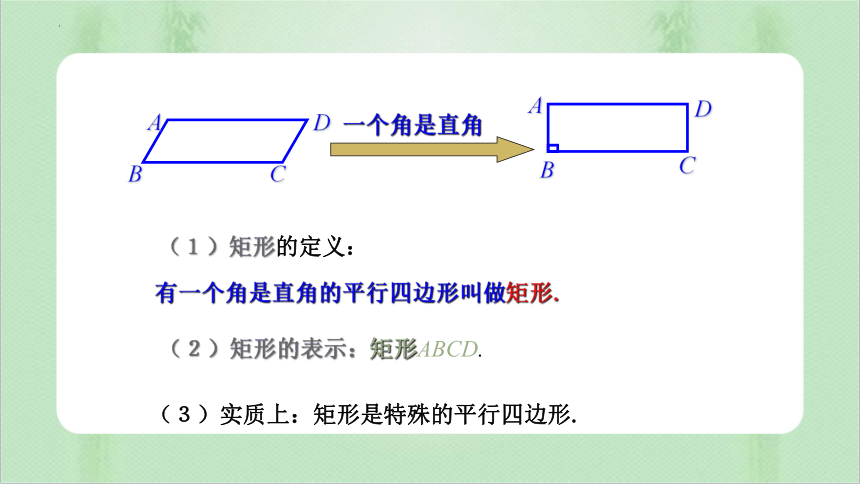
有一个角是直角的平行四边形叫做矩形.
A
B
C
D
(1)矩形的定义:
(3)实质上:矩形是特殊的平行四边形.
(2)矩形的表示:矩形ABCD.
一个角是直角
小学里学过的长方形、正方形都是矩形.
想一想:
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形?
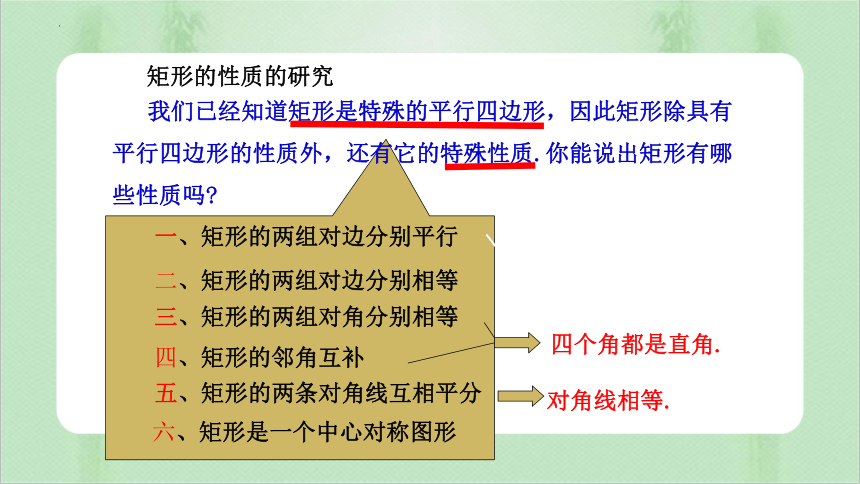
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
五、矩形的两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
六、矩形是一个中心对称图形
四个角都是直角.
对角线相等.
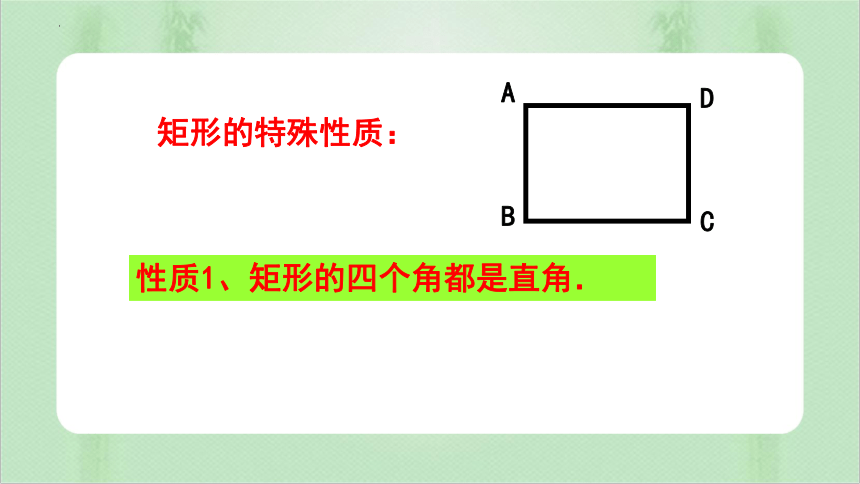
猜想1、矩形的四个角都是直角.
矩形的特殊性质:
性质1、矩形的四个角都是直角.
A
B
C
D
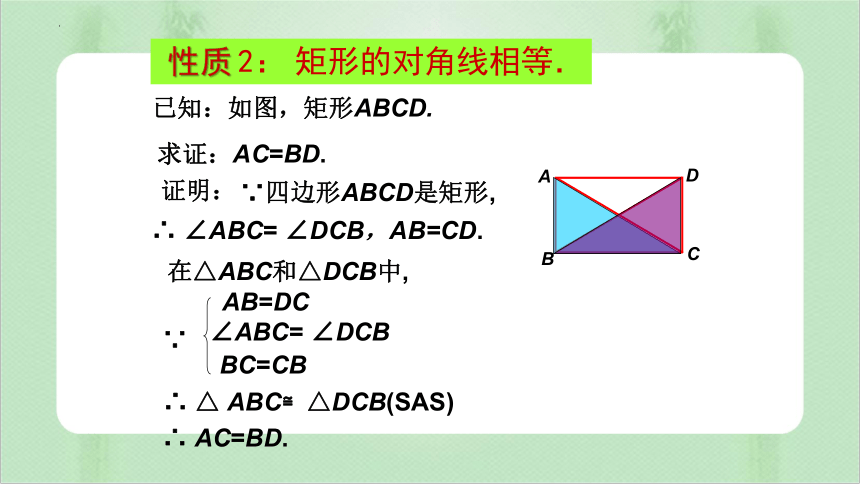
已知:如图,矩形ABCD.
A
D
B
C
∴ AC=BD.
∵四边形ABCD是矩形,
证明:
∴ ∠ABC= ∠DCB,AB=CD.
∴ △ ABC≌△DCB(SAS)
在△ABC和△DCB中,
AB=DC
∠ABC= ∠DCB
BC=CB
∵
求证:AC=BD.
2: 矩形的对角线相等.
性质
矩形的特殊性质
性质1、矩形的四个角都是直角.
性质2、矩形的两条对角线相等.
几何语言:
∵四边形ABCD是矩形
AC = BD
∴∠A=∠B=∠C=∠D=90°
思考:矩形ABCD是轴对称图形吗?
它的对称轴有几条?
矩形是中心对称图形吗?对称中心是?
A
B
C
D
E
F
G
H
.
探索矩形的对称性
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
考考大家:如图,矩形ABCD中,对角线AC、BD相交于点O,则OC=OB=OD成立吗?
△BCD中,∵∠BCD=90°,O是BD上的中点
∴CO = BD
例1:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4
∴矩形的对角线长 AC=BD=2OA=8
D
C
B
A
O
例2:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形的边长.(精确到0.01㎝)
A
B
O
C
D
解:
在矩形ABCD中,
∵ ∠AOD=120°
∴ ∠AOB=60°
∵OA=OB
∴ △AOB为等边三角形
∴AB=OA= AC=4cm
在Rt△ABC中,
≈6.93(cm)
BC=
=
=
方法小结: 如果矩形两对角 线的夹角是60°或120°,
则其中必有等边三角形.
例3、已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
分析:FM为Rt△BFC的斜边上的中线,EM为Rt△BEC的斜边上的中线
边 角 对角线 对称性
平行四 边形
矩形
对边平行
且相等
对角相等,
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相平分且相等
中心对称图
形,轴对称
图形
这是矩形所特有的性质
O
D
C
B
A
相等的线段:
AB=CD,AD=BC,AC=BD, OA=OC=OB=OD= AC= BD.
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠OBA=∠ODC=∠OCD , ∠OAD=∠ODA=∠OBC=∠OCB.
已知四边形ABCD是矩形
O
D
C
B
A
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB △OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两条对
称轴,也是中心对称图形。
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
矩形的性质小结
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
A
D
学以致用
3、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm2
5
2.5
14
12
矩形的两条边和对角线构成一个 三角形, 是斜边.
求矩形的边长和对角线的问题可转化为直角三角形,利用 解决.
直角
对角线
勾股定理
实验:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形。
1.2 .2 矩形的判定
命题1:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
所以 AB=CD(平行四边形对边相等),BC=BC,
所以△ABC≌ △DCB(SSS),
因为四边形ABCD是平行四边形(已知),
在 △ABC和△DCB中,
AB=CD (已证)
BC=CB (已证)
AC=DB (已知)
所以∠ABC=∠DCB(全等三角形对应角相等).
又因为∠ABC+∠DCB=180°(平行四边形邻角互补),
所以∠ABC=90°(等式的性质),
又因为 四边形ABCD是平行四边形(已知),
所以四边形ABCD是矩形(矩形的定义).
A
B
C
D
对角线相等的平行四边形是矩形
矩形的判定方法:
几何语言:
因为AC=BD,四边形ABCD是平行四边形(已知)
所以四边形ABCD是矩形(对角线相等的平行四边形是矩形)
A
B
C
D
O
探究:
命题2:
有三个角是直角的四边形是矩形。
证明:
四边形ABCD中,∠A=∠B=∠C=90°;
已知:
四边形ABCD是矩形.
求证:
∵∠A=∠B=90°
∴∠A+∠B=180°
∴AD∥BC,
同理:AB∥CD,
∴四边形ABCD是平行四边形
又∵∠A=90°
∴四边形ABCD是矩形。
D
A
C
B
矩形的判定方法:
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
矩形有几种判定方法?
有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
方法总结:
1、判断下列命题是否正确,并说明理由。
(1)对角互补的平行四边形是矩形。
(2)一组邻角相等的平行四边形是矩形。
(3)对角线相等的四边形是矩形。
(4)内角都相等的四边形是矩形。
练一练
[问题]一张四边形纸板ABCD的形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
E
F
G
H
⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.
解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.
两条对角线互相垂直,AC⊥BD
例 一张四边形的纸板ABCD的形状如图(1),它的两条对角线互相垂直。如果要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可以怎么剪?
(
2
)
(
1
)
O
O
D
B
C
A
A
C
B
D
G
F
H
E
E
F
G
H
理由如下:
∵GH是△ACD的中位线
∴GH∥AC
1
2
3
∵AC⊥BD
∴∠1=90°
(三角形的中位线平行于第三边
且等于第三边的一半)
∴∠2=∠1=90°
∵EH是△ABD的中位线
∴EH∥BD
∴∠3=∠2=90°.
4
5
(三角形的中位线平行于第三边)
同理可得:∠4=90°, ∠5=90°
∴四边形EFGH是矩形.
(有三个角是直角的四边形是矩形)
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
2.下列四边形中不是矩形的是( )
A.有三个角是直角的四边形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形
C
C
【跟踪训练】
3.已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,则AC=_______ ㎝ OB=_______ ㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
1.如图,要使□ABCD成为矩形,需添
加的条件是( )
(A)AB=BC (B)AC⊥BD
(C)∠ABC=90° (D)∠1=∠2
【解析】选C.因为有一个角是直角的平行四边形是矩形.
2.如图,MN∥PQ,同旁内角的平分线AB,BC和AD,CD分别相
交于点B,D.
(1)猜想线段AC和BD间的关系是______;
(2)试用理由说明你的猜想.
【解析】(1)相等
(2)理由:因为MN∥PQ,AB,CB分别是∠MAC,∠PCA的平分线,
所以∠BAC+∠ACB=90°,
所以∠ABC=90°,
同理∠ADC=90°.
因为CB,CD分别是∠PCA,∠QCA的平分线,
所以∠BCA+∠DCA=90°,
所以∠BCD=90°,
所以四边形ABCD是矩形,
所以AC=BD.
3.如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
证明:∵AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD.
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且相等BD.
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
有一个角是直角的平行四边形是矩形.
定理1:对角线相等的平行四边形是矩形.
定理2:有三个角是直角的四边形是矩形.
运用定理进行计算和证明.
矩形的判定
定义
定理
矩形的判定小结
北师大版 九年级上册数学
第一章 特殊平行四边形
1.2 矩形的性质与判定
观察下面图形,长方形在生活中无处不在.
情景引入
1.2 .1 矩形的性质
思考 长方形跟我们前面学行四边形有什么关系?
你还能举出其他的例子吗?
合作学习
用6根火柴棒首尾相接摆成一个平行四边形(如图).
(1)能摆成多少个不同的平行四边形?
它们有什么共同特点?说出你的理由.
(2)在这些平行四边形中,有没有面积最大的一个平 行四边形?说出你的理由.
(3)这个面积最大的平行四边形的内角有什么特点?
a
α
A D
A D
B C
A D
A D
A
B
C
D
有一个角是直角的平行四边形叫做矩形.
A
B
C
D
(1)矩形的定义:
(3)实质上:矩形是特殊的平行四边形.
(2)矩形的表示:矩形ABCD.
一个角是直角
小学里学过的长方形、正方形都是矩形.
想一想:
你能举出在人们的日常生活和生产实践中,有哪些东西是矩形?
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
五、矩形的两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
四、矩形的邻角互补
六、矩形是一个中心对称图形
四个角都是直角.
对角线相等.
猜想1、矩形的四个角都是直角.
矩形的特殊性质:
性质1、矩形的四个角都是直角.
A
B
C
D
已知:如图,矩形ABCD.
A
D
B
C
∴ AC=BD.
∵四边形ABCD是矩形,
证明:
∴ ∠ABC= ∠DCB,AB=CD.
∴ △ ABC≌△DCB(SAS)
在△ABC和△DCB中,
AB=DC
∠ABC= ∠DCB
BC=CB
∵
求证:AC=BD.
2: 矩形的对角线相等.
性质
矩形的特殊性质
性质1、矩形的四个角都是直角.
性质2、矩形的两条对角线相等.
几何语言:
∵四边形ABCD是矩形
AC = BD
∴∠A=∠B=∠C=∠D=90°
思考:矩形ABCD是轴对称图形吗?
它的对称轴有几条?
矩形是中心对称图形吗?对称中心是?
A
B
C
D
E
F
G
H
.
探索矩形的对称性
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
考考大家:如图,矩形ABCD中,对角线AC、BD相交于点O,则OC=OB=OD成立吗?
△BCD中,∵∠BCD=90°,O是BD上的中点
∴CO = BD
例1:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长?
解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4
∴矩形的对角线长 AC=BD=2OA=8
D
C
B
A
O
例2:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形的边长.(精确到0.01㎝)
A
B
O
C
D
解:
在矩形ABCD中,
∵ ∠AOD=120°
∴ ∠AOB=60°
∵OA=OB
∴ △AOB为等边三角形
∴AB=OA= AC=4cm
在Rt△ABC中,
≈6.93(cm)
BC=
=
=
方法小结: 如果矩形两对角 线的夹角是60°或120°,
则其中必有等边三角形.
例3、已知:如图BE、CF是△ABC的两条高,M为BC的中点,分别连ME、MF
求证: (1)ME= BC (2)ME=MF
C
M
A
B
F
E
分析:FM为Rt△BFC的斜边上的中线,EM为Rt△BEC的斜边上的中线
边 角 对角线 对称性
平行四 边形
矩形
对边平行
且相等
对角相等,
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相平分且相等
中心对称图
形,轴对称
图形
这是矩形所特有的性质
O
D
C
B
A
相等的线段:
AB=CD,AD=BC,AC=BD, OA=OC=OB=OD= AC= BD.
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC,∠AOD=∠BOC,
∠OAB=∠OBA=∠ODC=∠OCD , ∠OAD=∠ODA=∠OBC=∠OCB.
已知四边形ABCD是矩形
O
D
C
B
A
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB △OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两条对
称轴,也是中心对称图形。
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
矩形的性质小结
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角相等
C.是轴对称图形 D.对角线互相垂直
A
D
学以致用
3、如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,BO= cm,
矩形的周长为 cm,
矩形的面积为 cm2
5
2.5
14
12
矩形的两条边和对角线构成一个 三角形, 是斜边.
求矩形的边长和对角线的问题可转化为直角三角形,利用 解决.
直角
对角线
勾股定理
实验:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形。
1.2 .2 矩形的判定
命题1:对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
所以 AB=CD(平行四边形对边相等),BC=BC,
所以△ABC≌ △DCB(SSS),
因为四边形ABCD是平行四边形(已知),
在 △ABC和△DCB中,
AB=CD (已证)
BC=CB (已证)
AC=DB (已知)
所以∠ABC=∠DCB(全等三角形对应角相等).
又因为∠ABC+∠DCB=180°(平行四边形邻角互补),
所以∠ABC=90°(等式的性质),
又因为 四边形ABCD是平行四边形(已知),
所以四边形ABCD是矩形(矩形的定义).
A
B
C
D
对角线相等的平行四边形是矩形
矩形的判定方法:
几何语言:
因为AC=BD,四边形ABCD是平行四边形(已知)
所以四边形ABCD是矩形(对角线相等的平行四边形是矩形)
A
B
C
D
O
探究:
命题2:
有三个角是直角的四边形是矩形。
证明:
四边形ABCD中,∠A=∠B=∠C=90°;
已知:
四边形ABCD是矩形.
求证:
∵∠A=∠B=90°
∴∠A+∠B=180°
∴AD∥BC,
同理:AB∥CD,
∴四边形ABCD是平行四边形
又∵∠A=90°
∴四边形ABCD是矩形。
D
A
C
B
矩形的判定方法:
有三个角是直角的四边形是矩形 .
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
矩形有几种判定方法?
有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
方法总结:
1、判断下列命题是否正确,并说明理由。
(1)对角互补的平行四边形是矩形。
(2)一组邻角相等的平行四边形是矩形。
(3)对角线相等的四边形是矩形。
(4)内角都相等的四边形是矩形。
练一练
[问题]一张四边形纸板ABCD的形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
E
F
G
H
⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.
解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.
两条对角线互相垂直,AC⊥BD
例 一张四边形的纸板ABCD的形状如图(1),它的两条对角线互相垂直。如果要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可以怎么剪?
(
2
)
(
1
)
O
O
D
B
C
A
A
C
B
D
G
F
H
E
E
F
G
H
理由如下:
∵GH是△ACD的中位线
∴GH∥AC
1
2
3
∵AC⊥BD
∴∠1=90°
(三角形的中位线平行于第三边
且等于第三边的一半)
∴∠2=∠1=90°
∵EH是△ABD的中位线
∴EH∥BD
∴∠3=∠2=90°.
4
5
(三角形的中位线平行于第三边)
同理可得:∠4=90°, ∠5=90°
∴四边形EFGH是矩形.
(有三个角是直角的四边形是矩形)
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角相等 B.对边相等
C.对角线相等 D.对角线互相平分
2.下列四边形中不是矩形的是( )
A.有三个角是直角的四边形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形
C
C
【跟踪训练】
3.已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,则AC=_______ ㎝ OB=_______ ㎝
(2)若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm
AB= _____cm
O
D
C
B
A
5
10
4
1.如图,要使□ABCD成为矩形,需添
加的条件是( )
(A)AB=BC (B)AC⊥BD
(C)∠ABC=90° (D)∠1=∠2
【解析】选C.因为有一个角是直角的平行四边形是矩形.
2.如图,MN∥PQ,同旁内角的平分线AB,BC和AD,CD分别相
交于点B,D.
(1)猜想线段AC和BD间的关系是______;
(2)试用理由说明你的猜想.
【解析】(1)相等
(2)理由:因为MN∥PQ,AB,CB分别是∠MAC,∠PCA的平分线,
所以∠BAC+∠ACB=90°,
所以∠ABC=90°,
同理∠ADC=90°.
因为CB,CD分别是∠PCA,∠QCA的平分线,
所以∠BCA+∠DCA=90°,
所以∠BCD=90°,
所以四边形ABCD是矩形,
所以AC=BD.
3.如图,△ABC中,AB=AC,AD是BC边上的高,AE是△BAC的外角平分线,DE∥AB交AE于点E,求证:四边形ADCE是矩形.
证明:∵AB=AC,AD⊥BC,
∴∠B=∠ACB,BD=DC.
∵AE是∠BAC的外角平分线,
∴∠FAE=∠EAC.
∵∠B+∠ACB=∠FAE+∠EAC,
∴∠B=∠ACB=∠FAE=∠EAC,
∴AE∥CD.
又∵DE∥AB,
∴四边形AEDB是平行四边形,
∴AE平行且相等BD.
又∵BD=DC,
∴AE平行且等于DC,
故四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴平行四边形ADCE是矩形.
有一个角是直角的平行四边形是矩形.
定理1:对角线相等的平行四边形是矩形.
定理2:有三个角是直角的四边形是矩形.
运用定理进行计算和证明.
矩形的判定
定义
定理
矩形的判定小结
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
