三角形复习一[下学期]
图片预览






文档简介
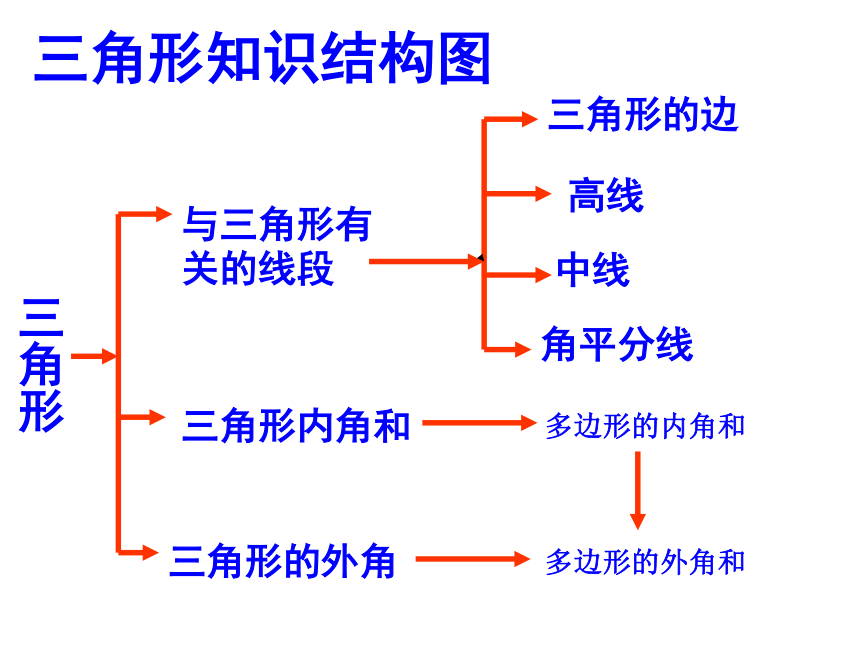
课件18张PPT。三角形复习(一)实验初中初三备课组复习要求 1、 理解三角形、三角形的顶点、边、内角、外角等概念;掌握三角形的角平分线、中线、高等概念,会画任意三角形的角平分线,中线和高。 4、会对三角形按边或按角进行分类。3、掌握三角形的内角和定理,三角形的外角等于与它不相 邻的两内角和、三角形的外角大于任何一个和它不相邻的内角及直角三角形两锐角互余的性质。2、理解三角形任何两边之和大于第三边的性质,会根据三条线段的长度判断它们能否构成三角形。三角形与三角形有关的线段三角形内角和三角形的外角三角形知识结构图三角形的边高线中线角平分线多边形的内角和多边形的外角和1. 三角形的三边关系:(1)三角形的任何两边之和大于第三边:知识要点(2)三角形的任何两边之差小于第三边(3)判断三条已知线段a、b、c能否组成三角形;
当a最长,且有b+c>a时,就可构成三角形。(4)确定三角形第三边的取值范围:两边之差<第三边<两边之和。2. 三角形的三条高线(或高线所在的直线)交于一点,锐角三角形三条高线交于三角形内部一点,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在的直线交于三角形外部一点。3. 三角形的三条中线交于三角形内部一点。4. 三角形的三条角平分线交于三角形内部一点。这是三角形中边的不等关系,是证明边的不等关系的依据,也是用来求三角形一边的范围的依据,
在实际中有广泛的应用。同时也用来判断三条线段能否构成三角形。注意要点: 1.在理解三角形的概念时应注意:
不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三条中线和角平分线都在三角形的内部,高有所不同:
锐角三角形的三条高在三角形内部,
直角三角形斜边上的高在三角形内部,另两条就是两直角边,
钝角三角形夹钝角的两边上的高在三角形外部,作这两条高时要先 延长钝角的边,再从锐角顶点作延长线的垂线段。 三角形有三条角平分线、三条中线、三条高,它们都是线段,而不是直线或射线;三角形有三条边,三个内角、六个外角,
其中外角是指三角形的一边与另一边的延长线所组成的角。
①按边分
三角形 不等边三角形
等腰三角形 等边三角形
底边和腰不相等的等腰三角形
②按角分
三角形 直角三角形
斜三角形 锐角三角形
钝角三角形
对概念进行分类,是明确概念的一种逻辑方法,在数学学习中有重要
作用,注意分类一定要做到“不重复”和“不遗漏”。
三角形的分类有两种方法练习一、选择题
1.下列说法中正确的是:
A.三角形一个角的平分线叫做三角形的角平分线。
B.在三角形中连结三个顶点和它的对边中点的直线叫三角形的中线。
C.从三角形的一个顶点出发向它的对边画的垂线叫三角形的高。
D.三角形的角平分线、中线、高都是线段。
2.一个三角形的三个内角中,至少有:
A.一个钝角 ? B.一个直角 C.三个锐角 D.两个锐角
3.长度为下列各组数值的三条线段,能构成三角形的是: A.7,5,12 ? B.6,8,15 C.4,5,6 D.8,4,3 4.△ABC中,若∠A+∠B=2∠C,则∠C的度数是: A.90° B.60° C.45° D.30° 5.三角形的一个外角小于和它相邻的内角,
则这个三角形为: A.锐角三角形 B.钝角三角形
C.直角三角形 D.不一定
√6.下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O
B、有一个外角是锐角的三角形是钝角三角形;
C、三角形的外角中必有两个角是钝角;
D、锐角三角形中两锐角的和必然小于60O;
7.三角形三个内角的度数分别是(x+y)°, (x-y)°,x°,且x>y>0,则该三角形有一个内角为 ( )
A、30° B、45° C、60° D、90°
8.把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A、只有一种截法 B、只有两种截法
C、有三种截法 D、有四种截法二、判断题 1.以平面上的任意三点为顶点,都可以画出一个三角形。
2.以10cm长为底的一个等腰三角形,
腰长一定要大于5cm。
3.等腰三角形一定是斜三角形。
4.如果三角形的一个内角等于其余两个内角的差,
那么此三角形一 定 是直角三角形。
5.三角形三内角的度数之比为2:3:4,
则这个三角形必为锐角三角形。 三、填空题:
1.一个三角形三个内角的度数比为1:2:1,则这个三角形是________
2.以16cm为腰的等腰三角形,底边长x的取值范围____________
3.等腰三角形两边长为25cm和12cm,那么周长是 ____________ 等腰直角三角形62cm0cm<X<32cm 4.如右图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,∠C= ____∠BED= 。
60°65°5、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形75°钝角6、如图,已知:AD是△ABC
的中线,△ABC的面积为50cm2 ,
则△ABD的面积是_______.25cm28、如图,在△ABC中,CE,BF是两条高,若∠A= 50° ,∠BCE= 30° ,则∠EBF的度数是 ,∠FBC的度数是 .40°20°7.一个三角形的三边长是整数,
周长为5,则最小边为 ;19.木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是 ;
10.小明绕五边形各边走一圈,他共转了 . 度。
11.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;三角形具有稳定性360(1)、(2)、(4)四.例讲例1.如图,∠ACD是△ABC的外角,CE平∠ACD,F是CA延长线上的一点,FG∥EC交AB延长线于G点,若∠ECD=62°,∠ABC=40°,求∠FGA的度数。 解:∵CE平分∠ACD,∠ECD=62° ∴∠ACD=124°
∴∠ACE=∠ECD=62° 又∵∠ABC=40° ∴∠BAC=∠ACD-∠ABC
= 124°-40°=84° (三角形一个外角等于和它不相邻的两内角和) ∵FG∥CE ∴∠F=∠ACE=62° 又∵∠BAC是△AFG的一个外角 ∴∠FGA=∠BAC-∠GFC=84°-62°=22° 例2.如图,BE平分∠ABD交CD于F,CE平分∠ACD交
AB于G,AB、CD交于点O,且∠A=48°,
∠D=46°,求∠BEC的度数。 解:∵∠AGC=∠EGB(对顶角相等) (∠A+∠ACG)=180°-∠AGC ∠BEC+∠EBG=180°-∠EBG
(三角形内角和定理) ∴∠A+∠ACG=∠BEC+∠EBG 同理∠D+∠DBF=∠BEC+∠ECF 又BE平分∠ABD ∴∠EBG=∠DBF 同理∠ECF=∠ACG ∴(∠A+∠ACG)+(∠D+∠DBF)=
(∠BEC+∠EBG)+(∠BEC+∠ECF) ∴∠A+∠D=2∠BEC ∴∠BEC= ???(∠A+∠D)= ???(48°+46°)=47° 练习1、如图∠ABC=56°,∠ACB=44°,AD是高,AE是角平分线。 求∠DAE的度数。
2、如图△ABC中,∠ABC、∠ACB的平分线交于O点,∠A=76°,求∠BOC的度数。 3.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数ABCD4.如图AD是△ABC的中线,AE是△ABD的中线,
BA=BD, 求证:AC=2AE。 ABCDEF
当a最长,且有b+c>a时,就可构成三角形。(4)确定三角形第三边的取值范围:两边之差<第三边<两边之和。2. 三角形的三条高线(或高线所在的直线)交于一点,锐角三角形三条高线交于三角形内部一点,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在的直线交于三角形外部一点。3. 三角形的三条中线交于三角形内部一点。4. 三角形的三条角平分线交于三角形内部一点。这是三角形中边的不等关系,是证明边的不等关系的依据,也是用来求三角形一边的范围的依据,
在实际中有广泛的应用。同时也用来判断三条线段能否构成三角形。注意要点: 1.在理解三角形的概念时应注意:
不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三条中线和角平分线都在三角形的内部,高有所不同:
锐角三角形的三条高在三角形内部,
直角三角形斜边上的高在三角形内部,另两条就是两直角边,
钝角三角形夹钝角的两边上的高在三角形外部,作这两条高时要先 延长钝角的边,再从锐角顶点作延长线的垂线段。 三角形有三条角平分线、三条中线、三条高,它们都是线段,而不是直线或射线;三角形有三条边,三个内角、六个外角,
其中外角是指三角形的一边与另一边的延长线所组成的角。
①按边分
三角形 不等边三角形
等腰三角形 等边三角形
底边和腰不相等的等腰三角形
②按角分
三角形 直角三角形
斜三角形 锐角三角形
钝角三角形
对概念进行分类,是明确概念的一种逻辑方法,在数学学习中有重要
作用,注意分类一定要做到“不重复”和“不遗漏”。
三角形的分类有两种方法练习一、选择题
1.下列说法中正确的是:
A.三角形一个角的平分线叫做三角形的角平分线。
B.在三角形中连结三个顶点和它的对边中点的直线叫三角形的中线。
C.从三角形的一个顶点出发向它的对边画的垂线叫三角形的高。
D.三角形的角平分线、中线、高都是线段。
2.一个三角形的三个内角中,至少有:
A.一个钝角 ? B.一个直角 C.三个锐角 D.两个锐角
3.长度为下列各组数值的三条线段,能构成三角形的是: A.7,5,12 ? B.6,8,15 C.4,5,6 D.8,4,3 4.△ABC中,若∠A+∠B=2∠C,则∠C的度数是: A.90° B.60° C.45° D.30° 5.三角形的一个外角小于和它相邻的内角,
则这个三角形为: A.锐角三角形 B.钝角三角形
C.直角三角形 D.不一定
√6.下列说法中,错误的是( )
A、一个三角形中至少有一个角不大于60O
B、有一个外角是锐角的三角形是钝角三角形;
C、三角形的外角中必有两个角是钝角;
D、锐角三角形中两锐角的和必然小于60O;
7.三角形三个内角的度数分别是(x+y)°, (x-y)°,x°,且x>y>0,则该三角形有一个内角为 ( )
A、30° B、45° C、60° D、90°
8.把14cm长的细铁丝截成三段,围成不等边三角形,并且使三边长均为整数,那么( )
A、只有一种截法 B、只有两种截法
C、有三种截法 D、有四种截法二、判断题 1.以平面上的任意三点为顶点,都可以画出一个三角形。
2.以10cm长为底的一个等腰三角形,
腰长一定要大于5cm。
3.等腰三角形一定是斜三角形。
4.如果三角形的一个内角等于其余两个内角的差,
那么此三角形一 定 是直角三角形。
5.三角形三内角的度数之比为2:3:4,
则这个三角形必为锐角三角形。 三、填空题:
1.一个三角形三个内角的度数比为1:2:1,则这个三角形是________
2.以16cm为腰的等腰三角形,底边长x的取值范围____________
3.等腰三角形两边长为25cm和12cm,那么周长是 ____________ 等腰直角三角形62cm0cm<X<32cm 4.如右图,AD是BC边上的高,BE是 △ ABD的角平分线,∠1=40°,∠2=30°,∠C= ____∠BED= 。
60°65°5、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则∠C的外角为_____度,这个三角形是____三角形75°钝角6、如图,已知:AD是△ABC
的中线,△ABC的面积为50cm2 ,
则△ABD的面积是_______.25cm28、如图,在△ABC中,CE,BF是两条高,若∠A= 50° ,∠BCE= 30° ,则∠EBF的度数是 ,∠FBC的度数是 .40°20°7.一个三角形的三边长是整数,
周长为5,则最小边为 ;19.木工师傅做完门框后,为防止变形,通常在角上钉一斜条,根据是 ;
10.小明绕五边形各边走一圈,他共转了 . 度。
11.下列正多边形(1)正三角形(2)正方形(3)正五边形(4)正六边形,其中用一种正多边形能镶嵌成平面图案的是
;三角形具有稳定性360(1)、(2)、(4)四.例讲例1.如图,∠ACD是△ABC的外角,CE平∠ACD,F是CA延长线上的一点,FG∥EC交AB延长线于G点,若∠ECD=62°,∠ABC=40°,求∠FGA的度数。 解:∵CE平分∠ACD,∠ECD=62° ∴∠ACD=124°
∴∠ACE=∠ECD=62° 又∵∠ABC=40° ∴∠BAC=∠ACD-∠ABC
= 124°-40°=84° (三角形一个外角等于和它不相邻的两内角和) ∵FG∥CE ∴∠F=∠ACE=62° 又∵∠BAC是△AFG的一个外角 ∴∠FGA=∠BAC-∠GFC=84°-62°=22° 例2.如图,BE平分∠ABD交CD于F,CE平分∠ACD交
AB于G,AB、CD交于点O,且∠A=48°,
∠D=46°,求∠BEC的度数。 解:∵∠AGC=∠EGB(对顶角相等) (∠A+∠ACG)=180°-∠AGC ∠BEC+∠EBG=180°-∠EBG
(三角形内角和定理) ∴∠A+∠ACG=∠BEC+∠EBG 同理∠D+∠DBF=∠BEC+∠ECF 又BE平分∠ABD ∴∠EBG=∠DBF 同理∠ECF=∠ACG ∴(∠A+∠ACG)+(∠D+∠DBF)=
(∠BEC+∠EBG)+(∠BEC+∠ECF) ∴∠A+∠D=2∠BEC ∴∠BEC= ???(∠A+∠D)= ???(48°+46°)=47° 练习1、如图∠ABC=56°,∠ACB=44°,AD是高,AE是角平分线。 求∠DAE的度数。
2、如图△ABC中,∠ABC、∠ACB的平分线交于O点,∠A=76°,求∠BOC的度数。 3.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数ABCD4.如图AD是△ABC的中线,AE是△ABD的中线,
BA=BD, 求证:AC=2AE。 ABCDEF
同课章节目录
