一元一次不等式[上学期]
图片预览



文档简介
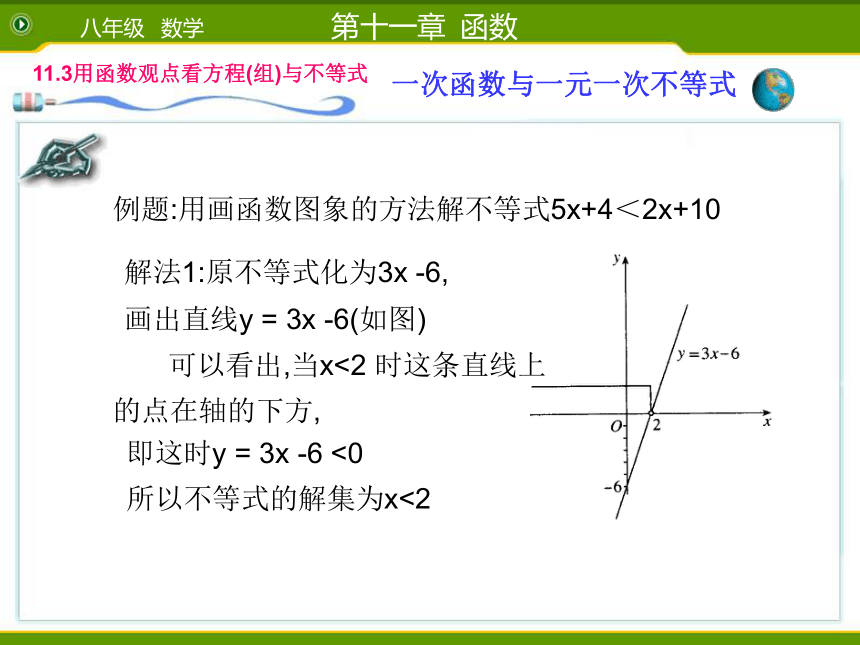
课件11张PPT。八年级数学一次函数与一元一次不等式人教实验版解(1)移项得:5x - 3x > 10 - 6合并,得 2x > 4∴原不等式的解是: x>2化系数为1,得x >2(2)作出函数 y = 2x -4 的图象(如图)从图知观察知,当x>2时 y 的值在x轴上方,即 y > 0因此当 x > 2 时函数的值大于0。例题:用画函数图象的方法解不等式5x+4<2x+10解法1:原不等式化为3x -6,画出直线y = 3x -6(如图) 可以看出,当x<2 时这条直线上
的点在轴的下方,即这时y = 3x -6 <0
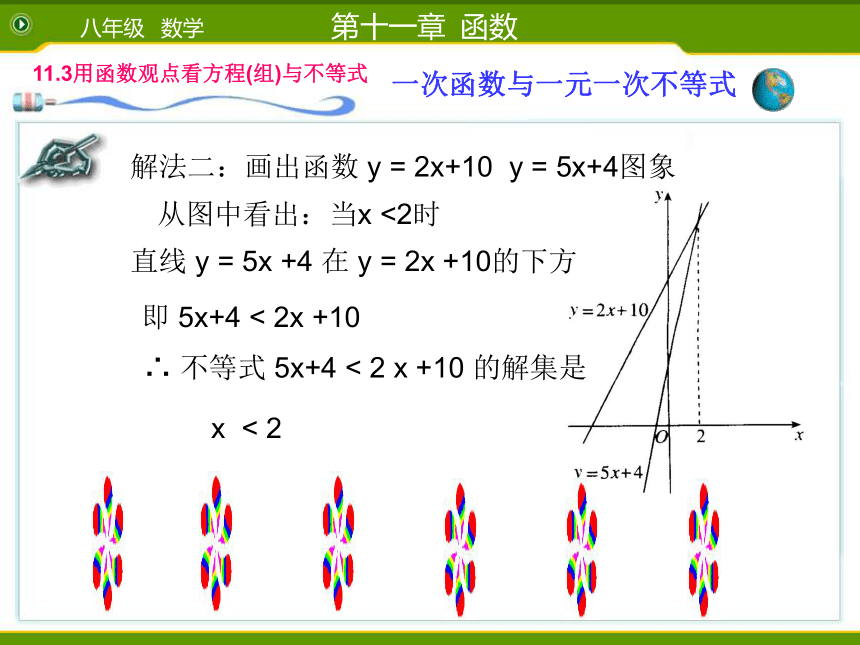
所以不等式的解集为x<2解法二:画出函数 y = 2x+10 y = 5x+4图象 从图中看出:当x <2时直线 y = 5x +4 在 y = 2x +10的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2已知一次函数 y = 2x+1,根据它的图象回答下列问题.
(1) x 取什么值时,函数值 y 为1?
(2) x 取什么值是,函数值 y 大于3?
(3) x 取什么值时,函数值 y 小于3?解:作出函数 y = 2x+1的图象及直线y = 3 (如图)y = 2x +1y= 3从图中可知:(1)当 x = 1 时,函数值 y 为1。(2)当x > 1 时,函数值 y 大于3。(3)当x <1 时,函数值 y 小于3。 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算. 2、当自变量 x 的取值满足什么条件时,
函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
3、用图象法解方程
(1)5x -1 = 2x + 5小结: 求一元一次不等式的解,可以看成某一个一次函数当
自变量取何值时,函数的值大于零或等于零。初步理解数形结合的内涵。作业: P45页第3、4题,P46页第7题。再见!
的点在轴的下方,即这时y = 3x -6 <0
所以不等式的解集为x<2解法二:画出函数 y = 2x+10 y = 5x+4图象 从图中看出:当x <2时直线 y = 5x +4 在 y = 2x +10的下方 即 5x+4 < 2x +10∴ 不等式 5x+4 < 2 x +10 的解集是x < 2已知一次函数 y = 2x+1,根据它的图象回答下列问题.
(1) x 取什么值时,函数值 y 为1?
(2) x 取什么值是,函数值 y 大于3?
(3) x 取什么值时,函数值 y 小于3?解:作出函数 y = 2x+1的图象及直线y = 3 (如图)y = 2x +1y= 3从图中可知:(1)当 x = 1 时,函数值 y 为1。(2)当x > 1 时,函数值 y 大于3。(3)当x <1 时,函数值 y 小于3。 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算. 2、当自变量 x 的取值满足什么条件时,
函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
3、用图象法解方程
(1)5x -1 = 2x + 5小结: 求一元一次不等式的解,可以看成某一个一次函数当
自变量取何值时,函数的值大于零或等于零。初步理解数形结合的内涵。作业: P45页第3、4题,P46页第7题。再见!
