菱形的性质与判定（三）

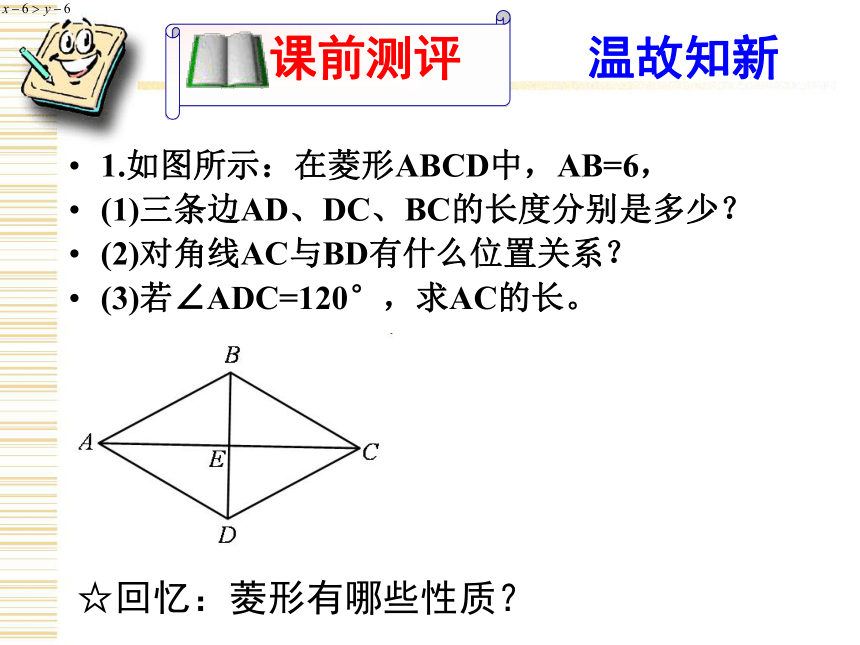
课件14张PPT。 甘肃省临泽县第四中学数学教研组第一章 特殊平行四边形 菱形的性质与判定（三）北师大版九年级数学上册温故知新1.如图所示：在菱形ABCD中，AB=6，
(1)三条边AD、DC、BC的长度分别是多少？
(2)对角线AC与BD有什么位置关系？
(3)若∠ADC=120°，求AC的长。
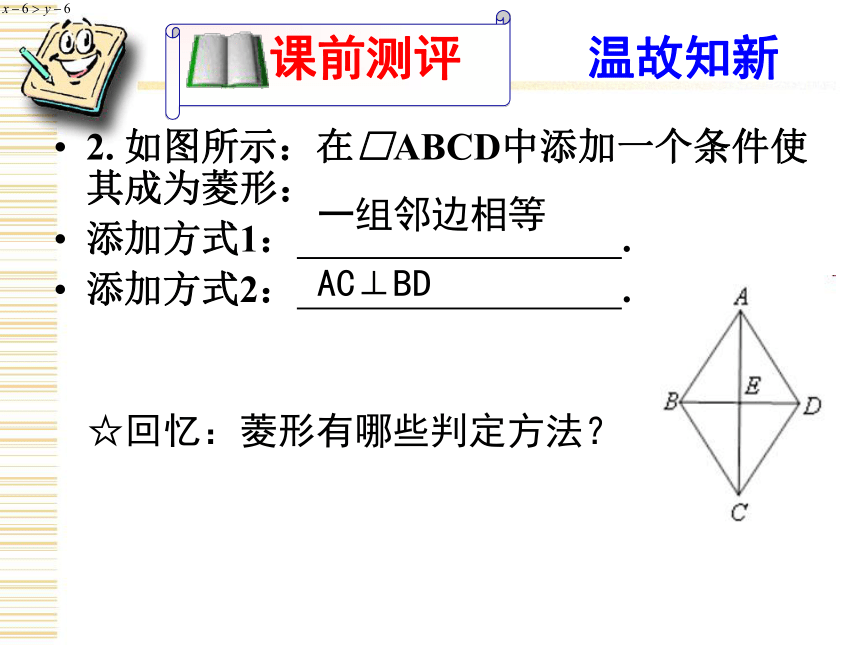
☆回忆：菱形有哪些性质？温故知新2. 如图所示：在□ABCD中添加一个条件使其成为菱形：
添加方式1： .
添加方式2： .☆回忆：菱形有哪些判定方法？一组邻边相等
AC⊥BD1.能灵活运用菱形的性质定理及判定定理解决一些相关问题，并掌握菱形面积的求法。
2.经历菱形性质定理及判定定理的应用过程，体会数形结合、转化等思想方法。
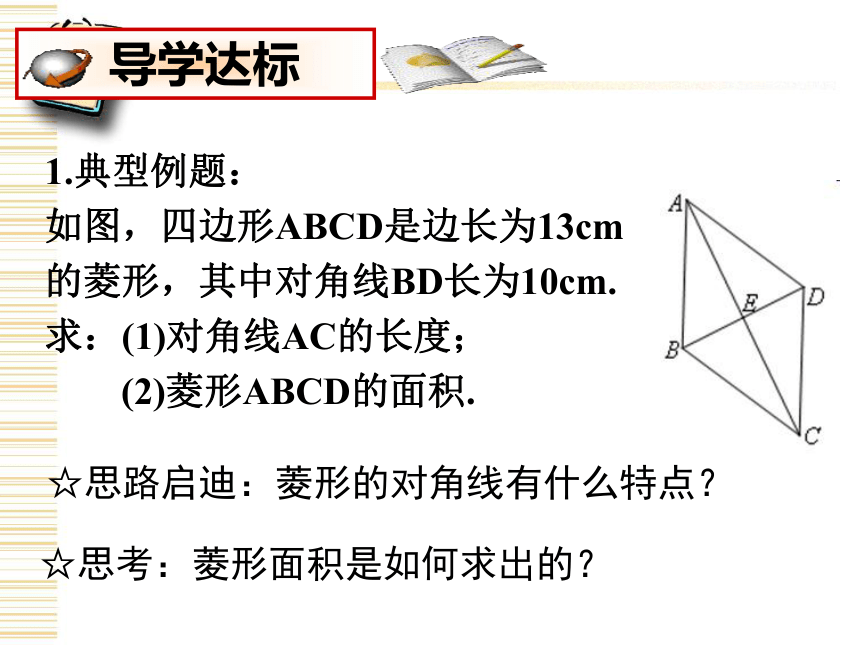
3.在学习过程中感受数学与生活的联系，增强学生的数学应用意识；在学习过程中通过小组合作交流，培养学生的合作交流能力与数学表达能力。1.典型例题：
如图，四边形ABCD是边长为13cm
的菱形，其中对角线BD长为10cm.
求：(1)对角线AC的长度；
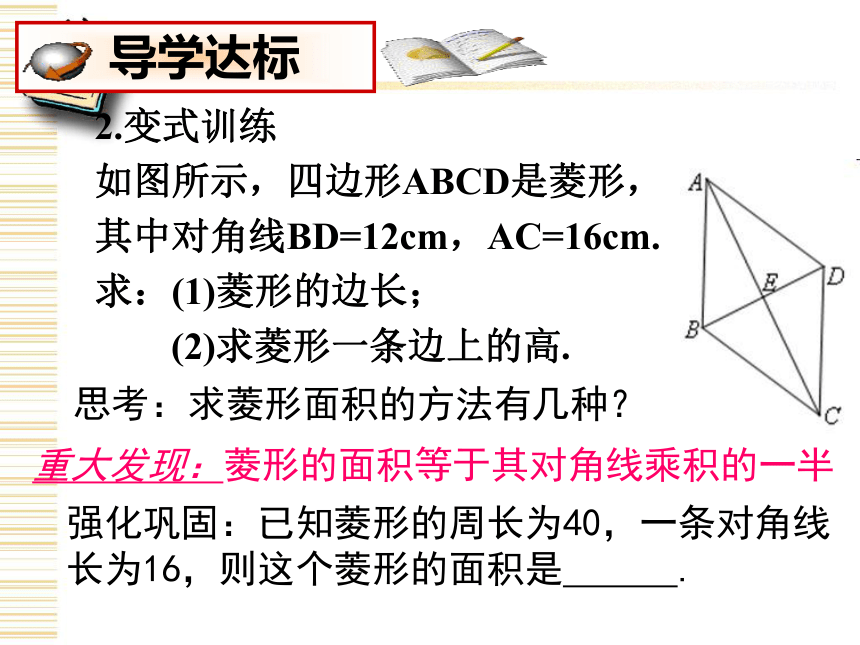
(2)菱形ABCD的面积.☆思路启迪：菱形的对角线有什么特点？☆思考：菱形面积是如何求出的？2.变式训练
如图所示，四边形ABCD是菱形，
其中对角线BD=12cm，AC=16cm.
求：(1)菱形的边长；
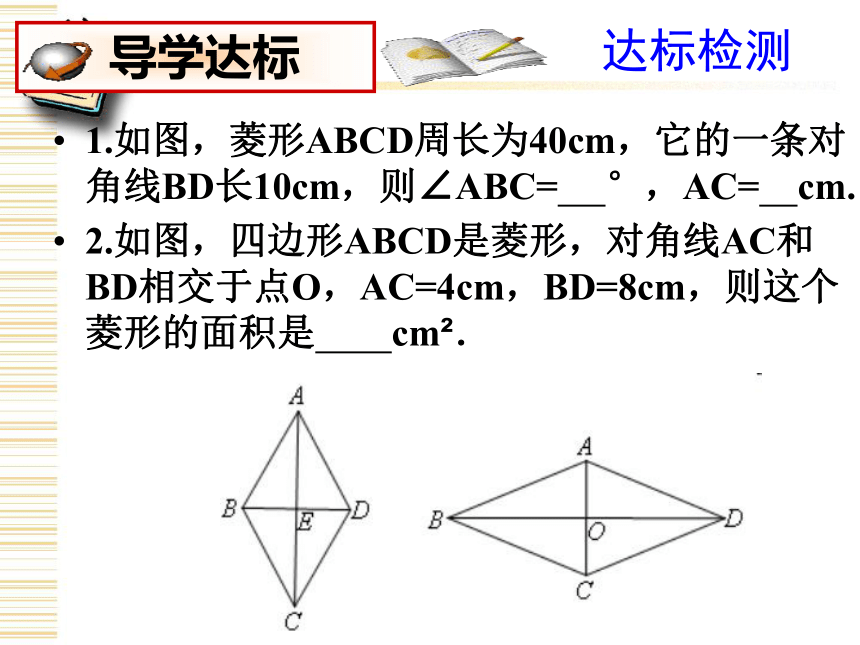
(2)求菱形一条边上的高.思考：求菱形面积的方法有几种？强化巩固：已知菱形的周长为40，一条对角线长为16，则这个菱形的面积是 .重大发现：菱形的面积等于其对角线乘积的一半达标检测 1.如图，菱形ABCD周长为40cm，它的一条对角线BD长10cm，则∠ABC= °，AC= cm.
2.如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC=4cm，BD=8cm，则这个菱形的面积是????????cm2．
达标检测3.已知，如图，在四边形ABCD中，AD=BC，点E、F、G、H分别是AB、CD、AC、BD的中点，四边形EGFH是（ ）
A.矩形 B.菱形 C.等腰梯形 D.正方形
4. 已知：如图，在菱形ABCD中，E、F分别是AB和BC上的点，且BE=BF，
求证：(1)△ADE≌CDF；(2) ∠DEF=∠DFE.拓展提高1.如图，两张等宽的纸条交叉重叠在一起，重叠部分ABCD是菱形吗？为什么？拓展提高2.如图你能用一张锐角三角形纸片ABC折出一个菱形，使∠A成为菱形一个内角吗？
3.如图，在Rt△ABC=90°，∠BAC=60°，BC的垂直平分线分别交BC和AB于点D、E，点F在DE延长线上，且AF=CE,求证：四边形ACEF是菱形.
拓展提高
4.如图，在四边形ABCD中，AD∥BC ，E为BC的中点，BC＝2AD，EA＝ED＝2，AC与ED相交于点F．当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．1.我学会了哪些知识？
2.我获得了哪些感受？我的收获我来说达标小结
习题1.3 知识技能　2、3、4
巩固强化