平行四边形判定1[下学期]
文档属性
| 名称 | 平行四边形判定1[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 720.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-08 00:00:00 | ||
图片预览





文档简介
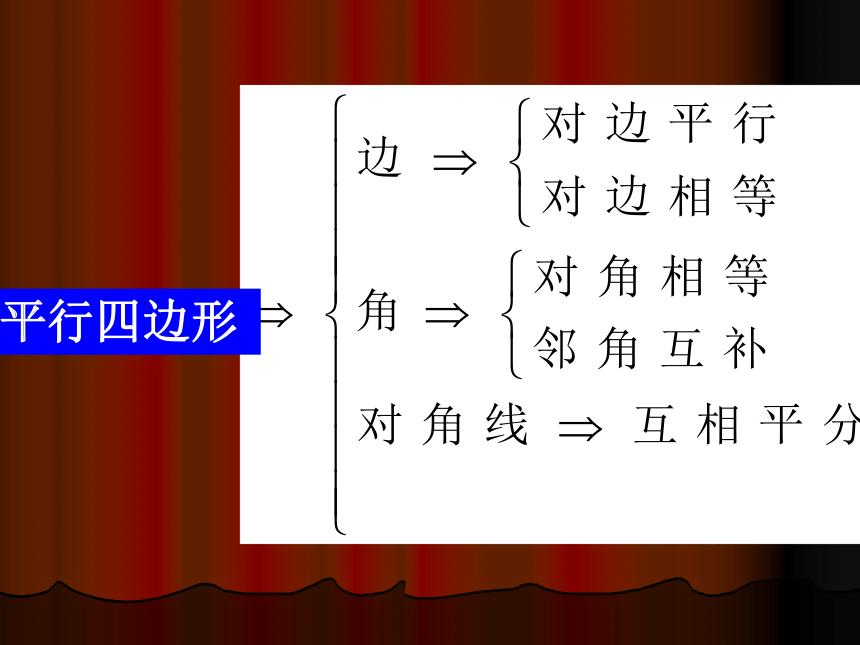
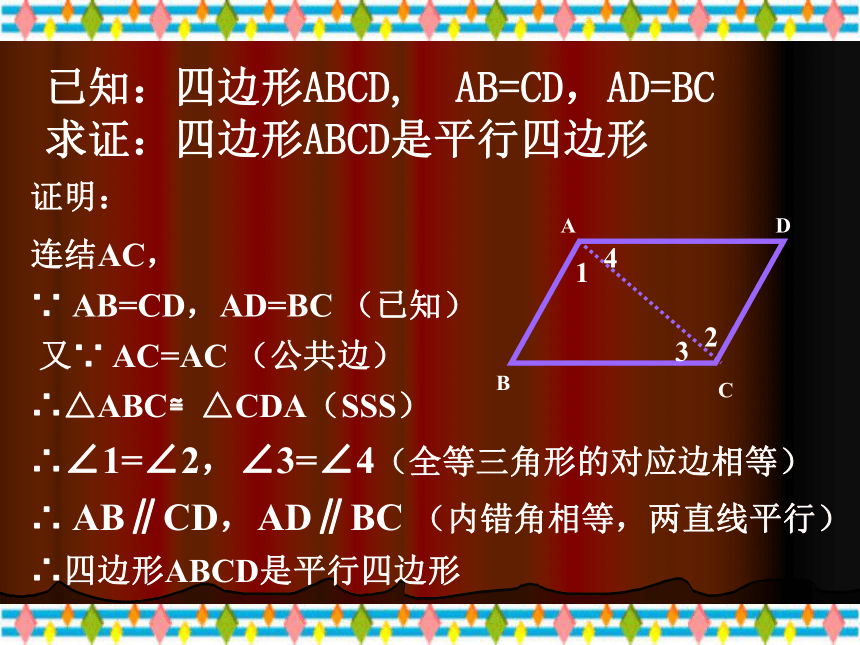
课件19张PPT。19.1.2 平行四边形的判定一.想一想有两组对边平行的四边形是平行四边形.1.平行四边形的对边相等;平行四边形的性质:2.平行四边形的对角相等;3.平行四边形的对角线互相平分.平行四边形的定义:定义:平行四边形的两组对边分别平行. 平行四边形二.试一试1.两组对边分别相等的四边形是平行四边形猜想:BDAC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形2134连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)证明:∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形两组对边分别相等的四边形
是平行四边形平行四边形判定定理1:三.比一比 平行四边形的两组对边相等;平行四边形性质定理1:平行四边形判定定理1: 两组对边分别相等的四边形
是平行四边形平行四边形的判定:定义:有两组对边平行的四边形是平行四边形.平行四边形的性质:定义:平行四边形的两组对边分别平行.三.比一比三.比一比性质:判定:1.平行四边形的对边
平行;
2.平行四边形的对边
相等;
3.平行四边形的对角
相等;
4.平行四边形的对角线互相平分.1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角相等的四边形是平行四边形4.对角线互相平分的四边形是平行四边形猜测:二.试一试2. 两条对角线互相平分的四边形是平行四边形猜想数学命题:BDACO已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形三.试一试四.探一探1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两条对角线互相平分的四边形是平行四边形;
平行四边形的判定方法:判定一个四边形是平行四边形需要几个条件?
你能从四边形的边、角、对角线的位置关系和数量关系出发,还找出其它的平行四边形的判定方法吗?4.一组对边平行且相等的四边形是平行四边形.一组对边平行且相等的四边形是平行四边形.猜想:1、请你识别下列四边形哪些是平行四边形?五.说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手练习2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战六.想一想:说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是:(2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”大胆猜想”-----”验证猜想(证明)”-----”得出结论”动动脑ABCDMNPQO2.已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点
求证 四边形MNPQ是平行四边形 如图,在 ?ABCD中,已知两条对角线相交于
点O, E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO
求证:四边形ABCD是平行四边形2134连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)证明:∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形两组对边分别相等的四边形
是平行四边形平行四边形判定定理1:三.比一比 平行四边形的两组对边相等;平行四边形性质定理1:平行四边形判定定理1: 两组对边分别相等的四边形
是平行四边形平行四边形的判定:定义:有两组对边平行的四边形是平行四边形.平行四边形的性质:定义:平行四边形的两组对边分别平行.三.比一比三.比一比性质:判定:1.平行四边形的对边
平行;
2.平行四边形的对边
相等;
3.平行四边形的对角
相等;
4.平行四边形的对角线互相平分.1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两组对角相等的四边形是平行四边形4.对角线互相平分的四边形是平行四边形猜测:二.试一试2. 两条对角线互相平分的四边形是平行四边形猜想数学命题:BDACO已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形三.试一试四.探一探1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.两条对角线互相平分的四边形是平行四边形;
平行四边形的判定方法:判定一个四边形是平行四边形需要几个条件?
你能从四边形的边、角、对角线的位置关系和数量关系出发,还找出其它的平行四边形的判定方法吗?4.一组对边平行且相等的四边形是平行四边形.一组对边平行且相等的四边形是平行四边形.猜想:1、请你识别下列四边形哪些是平行四边形?五.说一说⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝大显身手练习2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
3. 生物实验室有一块平行四边形的玻璃片,在做实验时,小明一不小心碰碎了一部分(如图所示),同学们!有没有办法把原来的平行四边形重新画出来?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战六.想一想:说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是:(2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”大胆猜想”-----”验证猜想(证明)”-----”得出结论”动动脑ABCDMNPQO2.已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD的中点
求证 四边形MNPQ是平行四边形 如图,在 ?ABCD中,已知两条对角线相交于
点O, E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。画一画ADCBEFGHO
