第二十三章 旋转全章教案
文档属性
| 名称 | 第二十三章 旋转全章教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-17 00:00:00 | ||
图片预览



文档简介
安国中学 九年级 数学导学案(初稿) ( http: / / www.21cnjy.com )
备课组长审阅
教研组长审签
学校审查
第8周初稿执笔:王惠
参与教师 李浩 王宁
授课教师
授课时间
授课班级
23.1图形的旋转(1)
学习目标
1、了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念
2、通过复习平移、轴对称的有关概念及性质,从生活中的数学开始,
经历观察,产生概念,应用概念解决一些实际问题.
教学重点: 旋转及对应点的有关概念及其应用
教学难点: 从活生生的数学中抽出概念
一、忆一忆
请同学们完成下面各题.
将如图所示的四边形ABCD平移,使点A的对应点为点C,作出平移后的
图形.
2、如图,已知△ABC和直线L,请你画出△ABC关于L的对
称图形△A′B′C′.
( http: / / www.21cnjy.com )
3.圆是轴对称图形吗?等腰三角形呢?你还能指出其它的吗?
4、总结:
(1)平移的有关概念及性质.
(2)如何画一个图形关于一条直线(对称轴)的对称图形,并口述它的一些
性质.
(3)什么叫轴对称图形?
二、探索新知 预习P56并思考
像这样,把一个图形绕着某 转动一个 的图形变换叫做旋转,
点O叫做 ,转动的角叫做 .
试一试 :
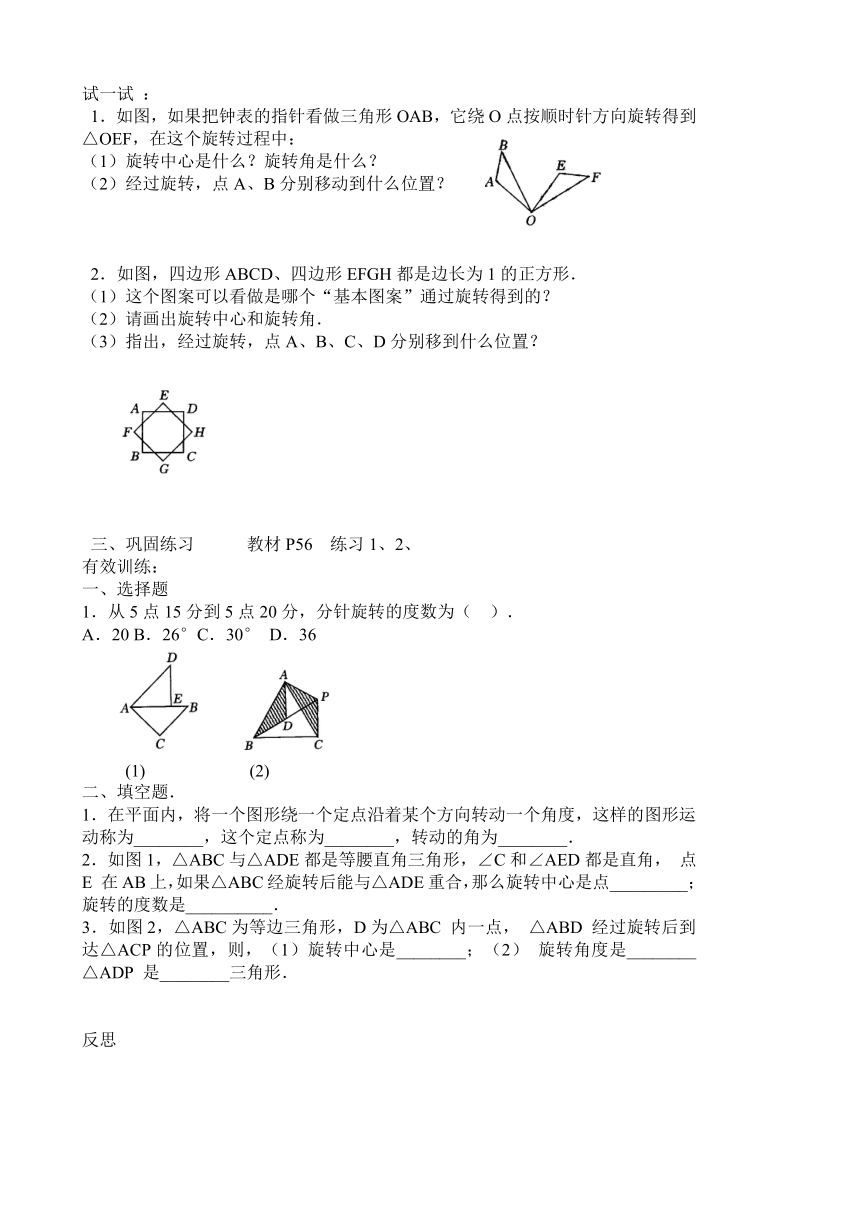
1.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
2.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角.
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
三、巩固练习 教材P56 练习1、2、
有效训练:
一、选择题
1.从5点15分到5点20分,分针旋转的度数为( ).
A.20 B.26°C.30° D.36
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
二、填空题.
1.在平面内,将一个图形绕一个定点沿着某个 ( http: / / www.21cnjy.com )方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.
2.如图1,△ABC与△ADE都是等腰直角 ( http: / / www.21cnjy.com )三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
3.如图2,△ABC为等边 ( http: / / www.21cnjy.com )三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________△ADP是________三角形.
反思
23.1 图形的旋转(2)
备课人 授课人 授课时间 授课班级
学习目标
理解对应点到旋转中心的距离相等;理解对 ( http: / / www.21cnjy.com )应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
先复习旋转及其旋转中心、旋转角和旋转的对应点概念,接着用操作几何、实验探究图形的旋转的基本性质.
教学重点: 图形的旋转的基本性质及其应用.
教学难点:运用操作实验几何得出图形的旋转的三条基本性质.
一、忆一忆:
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?
2.请独立完成下面的题目.
如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形?
上面的解题过程中,能否得出什么结论,请回答下面的问题:
(1).A、B、C、D、E、F到O点的距离是否相等?
(2).对应点与旋转中心所连线段的夹角∠BOC、∠COD、∠DOE、∠EOF、∠FOA是否相等?
(3).旋转前、后的图形这里指三角形△OAB、△OBC、△OCD、△ODE、△OEF、△OFA全等吗?
二、探索新知:
预习P57---58,并思考
1、(1)对应点到旋转中心的距离 ;
(2)对应点与旋转中心所连线段的夹角等于 ;
(3)旋转前、后的图形 .
2、例题的关键是: 。
三、试一试 :1.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.
2题图
2.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
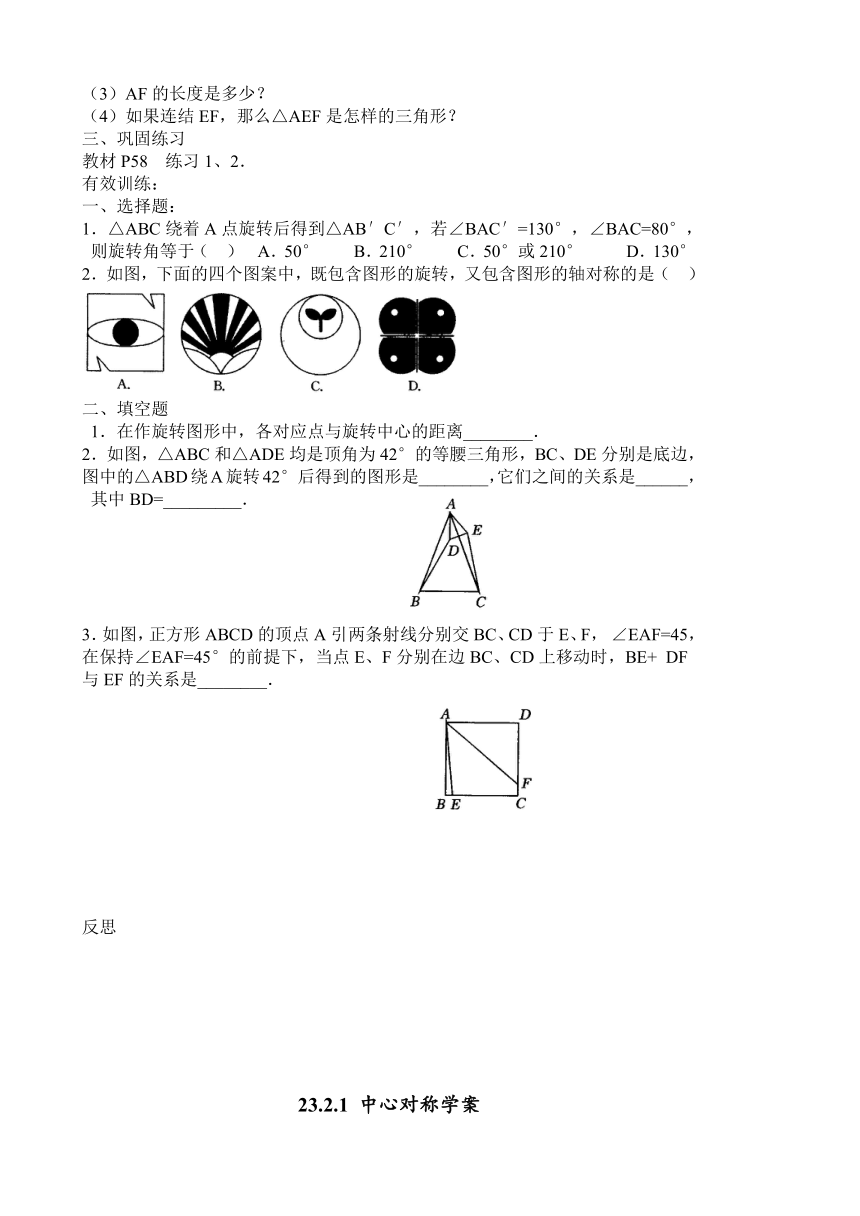
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
三、巩固练习
教材P58 练习1、2.
有效训练:
一、选择题:
1.△ABC绕着A点旋转后得到△A ( http: / / www.21cnjy.com )B′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( ) A.50° B.210° C.50°或210° D.130°
2.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
( http: / / www.21cnjy.com )
二、填空题
1.在作旋转图形中,各对应点与旋转中心的距离________.
2.如图,△ABC和△ADE均是顶 ( http: / / www.21cnjy.com )角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.
3.如图,正方形ABCD的顶点A引两条射线分 ( http: / / www.21cnjy.com )别交BC、CD于E、F,∠EAF=45,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是________.
反思
23.2.1 中心对称学案
备课人 授课人 授课时间 授课班级
【学习目标】
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质
学习重点:中心对称的概念和性质 学习难点:理解中心对称的性质
【学习过程】
活动一:复习回顾轴对称和旋转的有关知识
1、回忆什么是轴对称?成轴对称的两个图形有什么性质?
如果一个图形沿着_________对折后能与__________重合,则称这两个图形关于这条直线对称或轴对称。
成轴对称的图形,它们的对应点的连线被对称轴_________。
2、旋转有哪些性质?
对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________。
活动二:感知定义,探索性质
1、⑴把图①中一个图案绕点O旋转180°,你有什么发现?
⑵如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图① 图②
归纳:
中心对称的定义 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ):一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
活动三、 中心对称性质探索
动动手:(按下列步骤完成) 拿出三角板
⑴画出三角板内部的△ABC;
⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;
⑶移开三角板;
得出:△ABC与△A'B'C'关于O点对称。
思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?
⑵ △ABC与△A'B'C'有什么关系?
归纳:
中心对称的性质:
中心对称的两个图形,对称点所连线段经过_________,而且被对称中心__________;
中心对称的两个图形是 ;
当堂练习: 中心对称画法探索
1、⑴如图1,选择点O为对称中心,画出A点关于点O对称的点A'。
⑵如图2,选择点O为对称中心,画出与△ABC对称的△A'B'C'。
A
O
图1 图2
2、已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.
( http: / / www.21cnjy.com )
3、如图,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在C′处,求CC′的长度。
反思
23.2.2 中心对称图形
备课人 授课人 授课时间 授课班级
【学习目标】
了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
复习两个图形关于中心对称的有关概念,利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用.
学习重点:中心对称图形的有关概念及其它们的运用。
学习难点:区别关于中心对称的两个图形和中心对称图形。
【学习过程】
一、复习引入
关于中心对称的两个图形具有什么性质?
二、探索新知
1、将线段AB绕着点中点旋转180°,你有什么发现?
2、将ABCD绕它的两条对角线的交点O旋转180°,
你有什么发现?
归纳:
中心对称图形定义:一个图形 ( http: / / www.21cnjy.com )绕着某一个点___________,如果旋转后的图形能____________重合,那么这个图形叫做 ,这个点叫做___________。
三、巩固练习新课标第一网 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
1.下列图形中,是轴对称图形而不是中心对称图形的是( ).
( http: / / www.21cnjy.com )
2.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A B C D
3.下面各图中,哪些绕一点旋转180°后能与原来的图形重合 ( ).
( http: / / www.21cnjy.com )
A.①、④、⑤ B.①、③、⑤
C.②、③、⑤ D.②、④、⑤
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
5、下列四张扑克牌中,属于中心对称图案的是( )
( http: / / www.21cnjy.com )
6、下图是4个汽车的标志图案,其中是中心对称图形的是( )
( http: / / www.21cnjy.com )
A. B. C. D.
7、如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长。
反思
23.2.3关于原点对称的点的坐标
备课人 授课人 授课时间 授课班级
一、学习目标:
1、掌握在直角坐标系中关于原点对称的点的坐标的关系。
2、经历---猜想---验证的实践过程,积累数学活动的经验。
二、学习重点:探究关于原点对称的点的坐标的规律。
三、学习难点:关于原点对称的点的坐标的规律及运用.
四、学习过程:
(一)预习检测
1、学习准备:
(1)复习中心对称和中心对称图形的定义和性质;
(2)点P(x,y)关于Y轴对称的点的坐标P’( , );
(3)点P(x,y)关于X轴对称的点的坐标P’( , );
2、阅读课本P66——6 ( http: / / www.21cnjy.com )7,把你认为重要的、感兴趣的知识以及不理解的语句标记出来。(重要的勾画并标△号,感兴趣的只作勾画,不理解的勾画并标?号)
3、自学后完成问题:
(1)在直角坐标系中,两个关于原点对称 ( http: / / www.21cnjy.com )时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标P’( , )。
(2)点A(2,-3)关于原点对称的点的坐标A’( , );
点B(5,7)关于原点对称的点的坐标B’( , );
点C(-8,-1)关于原点对称的点的坐标C’( , )。
(二)合作探究
活动一:预习成果展示、交流.
活动二:如图,在直角坐标系中系中,已知A(-3,1)
B(-4,0)、C(0,3)、D(2,2)
E(3,-3)、F(-2,-2),作出A、B、C、
D、E、F点关于原点对称的点,并写出A’、B’
C’、D’、E’,F’的坐标。
回答:1、 这些坐标与已知点的坐标有什么关系?
2、谁能用三角形全等证明你们的结论。
[归纳] 在直角坐标系中,两个点关于 ( http: / / www.21cnjy.com )原点对称时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标为P’ 。
[引申] 若点P和点P’的坐标互为相反数,即P(x,y)和P’(-x,-y),则点P和点P’ 。
活动三:应用迁移 巩固提高
1、如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
2、已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC和它关于原点对称的图形。
3、下列各点中哪两个点关于原点对称?
A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)、G(-2,-1)。
4、已知点A(a,1) 和点A’(5,b)是关于原点O的对称点,求a+b 。
5、分别写出A(-5,0)、B(0 ( http: / / www.21cnjy.com ),2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)、G(-2,-1)关于X轴、Y轴和原点对称点的坐标。
(三)巩固练习
课本P68 第3、4题;
如图,在△ABC中,A(-5,4)、B(-6,2)、C(-2, 1),
① 画出△ABC X轴关于对称的△A1B1C1;;
② 将△ABC向右平移8个单位,画出平移后的△A2B2C2;
③ 将△ABC绕原点O旋转1800,画出旋转后的△A3B3C3;
④ 在△A1B1C1、△A2B2C2、△A3B3C3中, 和
成轴对称,对称轴是 。
⑤ △A1B1C1和△A2B2C2 (填“是”或“不是”)中心对称图形。
反思
第二十三章 旋转复习测试题
授课教师 授课时间 授课班级
一、精心选一选(每小题4分,共20分)
1.下列图形中,不是旋转图形的是 ( )
( http: / / www.21cnjy.com )
2.观察下列图案,其中旋转角最大的是 ( )
( http: / / www.21cnjy.com )
3.如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
4.下列命题中的真命题是 ( )
(A)全等的两个图形是中心对称图形. (B)关于中心对称的两个图形全等.
(C)中心对称图形都是轴对称图形. (D)轴对称图形都是中心对称图形.
5.有以下图形:平行四边形、矩形、等腰三 ( http: / / www.21cnjy.com )角形、线段、菱形,其中既是轴对称图形又是中心对称图形的有 ( )(A)5个. (B)4个. (C)3个. (D)2个.
二、耐心填一填(每小题4分,共40分)
6.关于某一点成中心对称的两个图形,对称点的连线都经过__________,并且被__________平分.
7.点(2,-3)关于原点对称的点的坐标是______.
8.请列出三个不同的牌面是中心对称图形的扑克牌:______、______、______.
9.如图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数是____.
10.一个正方形要绕它的中心至少旋转______度,才能与原来的图形重合.
11.如图,△ABC,△ACD,△A ( http: / / www.21cnjy.com )DE 是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转______度,才能与△ADE完全重合.
12.直线y=x+3上有一点P(m-5,2m),则P点关于原点的对称点P′为______.
13.如图是“靠右侧通道行驶”的交通标 ( http: / / www.21cnjy.com )志,若将图案绕其中心顺时针旋转90°,则得到的图案是“________________”交通标志(不画图案,只填含义).
14.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到的正方形EFCG,EF交AD于点H,那么DH的长为______.
15.已知平面直角坐标系上的三 ( http: / / www.21cnjy.com )个点O(0,0),A(-1,1),B(-1,0),将△ABO绕点O按顺时针旋转135°则点A,B的对应点A1,B1的坐标分别是A1(____,____),B1(____,____).
三、用心想一想(每题10分,共40分)
16.小金鱼在坐标系中的位置如图所示, ( http: / / www.21cnjy.com )将小金鱼身上的A、B、C、D、E、F的横坐标都乘以-1,纵坐标也都乘以-1,小金鱼跑到哪里去了 请在图上画出来.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17.如图,A点坐标为(3,3)将△ABC ( http: / / www.21cnjy.com )先向下移动4个单位得△A′B′C′,再将△A′B′C′绕点O逆时针旋转180°得△A′′B′′C′′,请你画出△A′B′C′和△A′′B′′C′′,并写出点A′′的坐标.
18.如图,网格中有一个四边 ( http: / / www.21cnjy.com )形和两个三角形.(1)请你画出三个图形关于点O的中心对称图形;(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.试问这个整体图形至少旋转多少度才能与自身重合
19.如图,在直角坐标系中,点P的坐标 ( http: / / www.21cnjy.com )为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′,(1)在图中画出线段OP′;(2)求P′的坐标和PP′的长度.
二次备课记录
B
A
C
O
A
B
_
B F
_
A E
_
C
_
D
_
O
备课组长审阅
教研组长审签
学校审查
第8周初稿执笔:王惠
参与教师 李浩 王宁
授课教师
授课时间
授课班级
23.1图形的旋转(1)
学习目标
1、了解旋转及其旋转中心和旋转角的概念,了解旋转对应点的概念
2、通过复习平移、轴对称的有关概念及性质,从生活中的数学开始,
经历观察,产生概念,应用概念解决一些实际问题.
教学重点: 旋转及对应点的有关概念及其应用
教学难点: 从活生生的数学中抽出概念
一、忆一忆
请同学们完成下面各题.
将如图所示的四边形ABCD平移,使点A的对应点为点C,作出平移后的
图形.
2、如图,已知△ABC和直线L,请你画出△ABC关于L的对
称图形△A′B′C′.
( http: / / www.21cnjy.com )
3.圆是轴对称图形吗?等腰三角形呢?你还能指出其它的吗?
4、总结:
(1)平移的有关概念及性质.
(2)如何画一个图形关于一条直线(对称轴)的对称图形,并口述它的一些
性质.
(3)什么叫轴对称图形?
二、探索新知 预习P56并思考
像这样,把一个图形绕着某 转动一个 的图形变换叫做旋转,
点O叫做 ,转动的角叫做 .
试一试 :
1.如图,如果把钟表的指针看做三角形OAB,它绕O点按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
2.如图,四边形ABCD、四边形EFGH都是边长为1的正方形.
(1)这个图案可以看做是哪个“基本图案”通过旋转得到的?
(2)请画出旋转中心和旋转角.
(3)指出,经过旋转,点A、B、C、D分别移到什么位置?
三、巩固练习 教材P56 练习1、2、
有效训练:
一、选择题
1.从5点15分到5点20分,分针旋转的度数为( ).
A.20 B.26°C.30° D.36
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2)
二、填空题.
1.在平面内,将一个图形绕一个定点沿着某个 ( http: / / www.21cnjy.com )方向转动一个角度,这样的图形运动称为________,这个定点称为________,转动的角为________.
2.如图1,△ABC与△ADE都是等腰直角 ( http: / / www.21cnjy.com )三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_________;旋转的度数是__________.
3.如图2,△ABC为等边 ( http: / / www.21cnjy.com )三角形,D为△ABC内一点,△ABD经过旋转后到达△ACP的位置,则,(1)旋转中心是________;(2)旋转角度是________△ADP是________三角形.
反思
23.1 图形的旋转(2)
备课人 授课人 授课时间 授课班级
学习目标
理解对应点到旋转中心的距离相等;理解对 ( http: / / www.21cnjy.com )应点与旋转中心所连线段的夹角等于旋转角;理解旋转前、后的图形全等.掌握以上三个图形的旋转的基本性质的运用.
先复习旋转及其旋转中心、旋转角和旋转的对应点概念,接着用操作几何、实验探究图形的旋转的基本性质.
教学重点: 图形的旋转的基本性质及其应用.
教学难点:运用操作实验几何得出图形的旋转的三条基本性质.
一、忆一忆:
1.什么叫旋转?什么叫旋转中心?什么叫旋转角?
2.请独立完成下面的题目.
如图,O是六个正三角形的公共顶点,正六边形ABCDEF能否看做是某条线段绕O点旋转若干次所形成的图形?
上面的解题过程中,能否得出什么结论,请回答下面的问题:
(1).A、B、C、D、E、F到O点的距离是否相等?
(2).对应点与旋转中心所连线段的夹角∠BOC、∠COD、∠DOE、∠EOF、∠FOA是否相等?
(3).旋转前、后的图形这里指三角形△OAB、△OBC、△OCD、△ODE、△OEF、△OFA全等吗?
二、探索新知:
预习P57---58,并思考
1、(1)对应点到旋转中心的距离 ;
(2)对应点与旋转中心所连线段的夹角等于 ;
(3)旋转前、后的图形 .
2、例题的关键是: 。
三、试一试 :1.如图,△ABC绕C点旋转后,顶点A的对应点为点D,试确定顶点B对应点的位置,以及旋转后的三角形.
2题图
2.如图,四边形ABCD是边长为1的正方形,且DE=,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连结EF,那么△AEF是怎样的三角形?
三、巩固练习
教材P58 练习1、2.
有效训练:
一、选择题:
1.△ABC绕着A点旋转后得到△A ( http: / / www.21cnjy.com )B′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( ) A.50° B.210° C.50°或210° D.130°
2.如图,下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是( )
( http: / / www.21cnjy.com )
二、填空题
1.在作旋转图形中,各对应点与旋转中心的距离________.
2.如图,△ABC和△ADE均是顶 ( http: / / www.21cnjy.com )角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是________,它们之间的关系是______,其中BD=_________.
3.如图,正方形ABCD的顶点A引两条射线分 ( http: / / www.21cnjy.com )别交BC、CD于E、F,∠EAF=45,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是________.
反思
23.2.1 中心对称学案
备课人 授课人 授课时间 授课班级
【学习目标】
1、通过具体实例认识中心对称,了解中心对称的概念
2、掌握中心对称的性质,理解对应点所连线段被对称中心平分的性质
学习重点:中心对称的概念和性质 学习难点:理解中心对称的性质
【学习过程】
活动一:复习回顾轴对称和旋转的有关知识
1、回忆什么是轴对称?成轴对称的两个图形有什么性质?
如果一个图形沿着_________对折后能与__________重合,则称这两个图形关于这条直线对称或轴对称。
成轴对称的图形,它们的对应点的连线被对称轴_________。
2、旋转有哪些性质?
对应点到旋转中心的距离___________对应点与旋转中心所连线段的夹角___________旋转前、后的图形___________。
活动二:感知定义,探索性质
1、⑴把图①中一个图案绕点O旋转180°,你有什么发现?
⑵如图②,线段AC、BD相交于点O,OA=OC,OB=OD。把△OCD绕点O旋转180°,你有什么发现?
图① 图②
归纳:
中心对称的定义 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ):一个图形绕着某一个点___________,如果它能与____________重合,就说这两个图形关于这个点对称或中心对称,这个点叫做___________,两个图形中的对应点叫做关于中心的_________。
活动三、 中心对称性质探索
动动手:(按下列步骤完成) 拿出三角板
⑴画出三角板内部的△ABC;
⑵以三角板的一个顶点O为中心,把三角板旋转180°,画出△AˊBˊCˊ;
⑶移开三角板;
得出:△ABC与△A'B'C'关于O点对称。
思考:⑴分别连接对称点AA'、BB'、CC'。点O在线段AA'上吗?如果在,在什么位置?
⑵ △ABC与△A'B'C'有什么关系?
归纳:
中心对称的性质:
中心对称的两个图形,对称点所连线段经过_________,而且被对称中心__________;
中心对称的两个图形是 ;
当堂练习: 中心对称画法探索
1、⑴如图1,选择点O为对称中心,画出A点关于点O对称的点A'。
⑵如图2,选择点O为对称中心,画出与△ABC对称的△A'B'C'。
A
O
图1 图2
2、已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心,并简要说明理由.
( http: / / www.21cnjy.com )
3、如图,在△ABC中,∠B=90°,∠C=30°,AB=1,将△ABC绕顶点A旋转180°,点C落在C′处,求CC′的长度。
反思
23.2.2 中心对称图形
备课人 授课人 授课时间 授课班级
【学习目标】
了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
复习两个图形关于中心对称的有关概念,利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用.
学习重点:中心对称图形的有关概念及其它们的运用。
学习难点:区别关于中心对称的两个图形和中心对称图形。
【学习过程】
一、复习引入
关于中心对称的两个图形具有什么性质?
二、探索新知
1、将线段AB绕着点中点旋转180°,你有什么发现?
2、将ABCD绕它的两条对角线的交点O旋转180°,
你有什么发现?
归纳:
中心对称图形定义:一个图形 ( http: / / www.21cnjy.com )绕着某一个点___________,如果旋转后的图形能____________重合,那么这个图形叫做 ,这个点叫做___________。
三、巩固练习新课标第一网 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
1.下列图形中,是轴对称图形而不是中心对称图形的是( ).
( http: / / www.21cnjy.com )
2.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A B C D
3.下面各图中,哪些绕一点旋转180°后能与原来的图形重合 ( ).
( http: / / www.21cnjy.com )
A.①、④、⑤ B.①、③、⑤
C.②、③、⑤ D.②、④、⑤
4.如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
5、下列四张扑克牌中,属于中心对称图案的是( )
( http: / / www.21cnjy.com )
6、下图是4个汽车的标志图案,其中是中心对称图形的是( )
( http: / / www.21cnjy.com )
A. B. C. D.
7、如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长。
反思
23.2.3关于原点对称的点的坐标
备课人 授课人 授课时间 授课班级
一、学习目标:
1、掌握在直角坐标系中关于原点对称的点的坐标的关系。
2、经历---猜想---验证的实践过程,积累数学活动的经验。
二、学习重点:探究关于原点对称的点的坐标的规律。
三、学习难点:关于原点对称的点的坐标的规律及运用.
四、学习过程:
(一)预习检测
1、学习准备:
(1)复习中心对称和中心对称图形的定义和性质;
(2)点P(x,y)关于Y轴对称的点的坐标P’( , );
(3)点P(x,y)关于X轴对称的点的坐标P’( , );
2、阅读课本P66——6 ( http: / / www.21cnjy.com )7,把你认为重要的、感兴趣的知识以及不理解的语句标记出来。(重要的勾画并标△号,感兴趣的只作勾画,不理解的勾画并标?号)
3、自学后完成问题:
(1)在直角坐标系中,两个关于原点对称 ( http: / / www.21cnjy.com )时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标P’( , )。
(2)点A(2,-3)关于原点对称的点的坐标A’( , );
点B(5,7)关于原点对称的点的坐标B’( , );
点C(-8,-1)关于原点对称的点的坐标C’( , )。
(二)合作探究
活动一:预习成果展示、交流.
活动二:如图,在直角坐标系中系中,已知A(-3,1)
B(-4,0)、C(0,3)、D(2,2)
E(3,-3)、F(-2,-2),作出A、B、C、
D、E、F点关于原点对称的点,并写出A’、B’
C’、D’、E’,F’的坐标。
回答:1、 这些坐标与已知点的坐标有什么关系?
2、谁能用三角形全等证明你们的结论。
[归纳] 在直角坐标系中,两个点关于 ( http: / / www.21cnjy.com )原点对称时,它们的坐标 ,即点P(x,y)关于原点对称的点的坐标为P’ 。
[引申] 若点P和点P’的坐标互为相反数,即P(x,y)和P’(-x,-y),则点P和点P’ 。
活动三:应用迁移 巩固提高
1、如图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
2、已知△ABC,A(1,2),B(-1,3),C(-2,4)利用关于原点对称的点的坐标的特点,作出△ABC和它关于原点对称的图形。
3、下列各点中哪两个点关于原点对称?
A(-5,0)、B(0,2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)、G(-2,-1)。
4、已知点A(a,1) 和点A’(5,b)是关于原点O的对称点,求a+b 。
5、分别写出A(-5,0)、B(0 ( http: / / www.21cnjy.com ),2)、C(2,-1)、D(2,0)、E(0,5)、F(-2,1)、G(-2,-1)关于X轴、Y轴和原点对称点的坐标。
(三)巩固练习
课本P68 第3、4题;
如图,在△ABC中,A(-5,4)、B(-6,2)、C(-2, 1),
① 画出△ABC X轴关于对称的△A1B1C1;;
② 将△ABC向右平移8个单位,画出平移后的△A2B2C2;
③ 将△ABC绕原点O旋转1800,画出旋转后的△A3B3C3;
④ 在△A1B1C1、△A2B2C2、△A3B3C3中, 和
成轴对称,对称轴是 。
⑤ △A1B1C1和△A2B2C2 (填“是”或“不是”)中心对称图形。
反思
第二十三章 旋转复习测试题
授课教师 授课时间 授课班级
一、精心选一选(每小题4分,共20分)
1.下列图形中,不是旋转图形的是 ( )
( http: / / www.21cnjy.com )
2.观察下列图案,其中旋转角最大的是 ( )
( http: / / www.21cnjy.com )
3.如图,将正方形图案绕中心O旋转180°后,得到的图案是 ( )
4.下列命题中的真命题是 ( )
(A)全等的两个图形是中心对称图形. (B)关于中心对称的两个图形全等.
(C)中心对称图形都是轴对称图形. (D)轴对称图形都是中心对称图形.
5.有以下图形:平行四边形、矩形、等腰三 ( http: / / www.21cnjy.com )角形、线段、菱形,其中既是轴对称图形又是中心对称图形的有 ( )(A)5个. (B)4个. (C)3个. (D)2个.
二、耐心填一填(每小题4分,共40分)
6.关于某一点成中心对称的两个图形,对称点的连线都经过__________,并且被__________平分.
7.点(2,-3)关于原点对称的点的坐标是______.
8.请列出三个不同的牌面是中心对称图形的扑克牌:______、______、______.
9.如图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数是____.
10.一个正方形要绕它的中心至少旋转______度,才能与原来的图形重合.
11.如图,△ABC,△ACD,△A ( http: / / www.21cnjy.com )DE 是三个全等的正三角形,那么△ABC绕着顶点A沿逆时针方向至少旋转______度,才能与△ADE完全重合.
12.直线y=x+3上有一点P(m-5,2m),则P点关于原点的对称点P′为______.
13.如图是“靠右侧通道行驶”的交通标 ( http: / / www.21cnjy.com )志,若将图案绕其中心顺时针旋转90°,则得到的图案是“________________”交通标志(不画图案,只填含义).
14.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到的正方形EFCG,EF交AD于点H,那么DH的长为______.
15.已知平面直角坐标系上的三 ( http: / / www.21cnjy.com )个点O(0,0),A(-1,1),B(-1,0),将△ABO绕点O按顺时针旋转135°则点A,B的对应点A1,B1的坐标分别是A1(____,____),B1(____,____).
三、用心想一想(每题10分,共40分)
16.小金鱼在坐标系中的位置如图所示, ( http: / / www.21cnjy.com )将小金鱼身上的A、B、C、D、E、F的横坐标都乘以-1,纵坐标也都乘以-1,小金鱼跑到哪里去了 请在图上画出来.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
17.如图,A点坐标为(3,3)将△ABC ( http: / / www.21cnjy.com )先向下移动4个单位得△A′B′C′,再将△A′B′C′绕点O逆时针旋转180°得△A′′B′′C′′,请你画出△A′B′C′和△A′′B′′C′′,并写出点A′′的坐标.
18.如图,网格中有一个四边 ( http: / / www.21cnjy.com )形和两个三角形.(1)请你画出三个图形关于点O的中心对称图形;(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.试问这个整体图形至少旋转多少度才能与自身重合
19.如图,在直角坐标系中,点P的坐标 ( http: / / www.21cnjy.com )为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′,(1)在图中画出线段OP′;(2)求P′的坐标和PP′的长度.
二次备课记录
B
A
C
O
A
B
_
B F
_
A E
_
C
_
D
_
O
同课章节目录
