14.2.2完全平方公式 课件(共15张PPT)2022-2023学年人教版八年级数学上册
文档属性
| 名称 | 14.2.2完全平方公式 课件(共15张PPT)2022-2023学年人教版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 693.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 15:59:40 | ||
图片预览




文档简介
(共15张PPT)
完全平方公式
义务教育教科书八年级上册14.2.2
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事非。
———华罗庚
小苏
小菲
1
谁买蛋糕更划算
通过这个图形,你能利用面积关系计算(a+b) 吗?
b
b
a
a
2
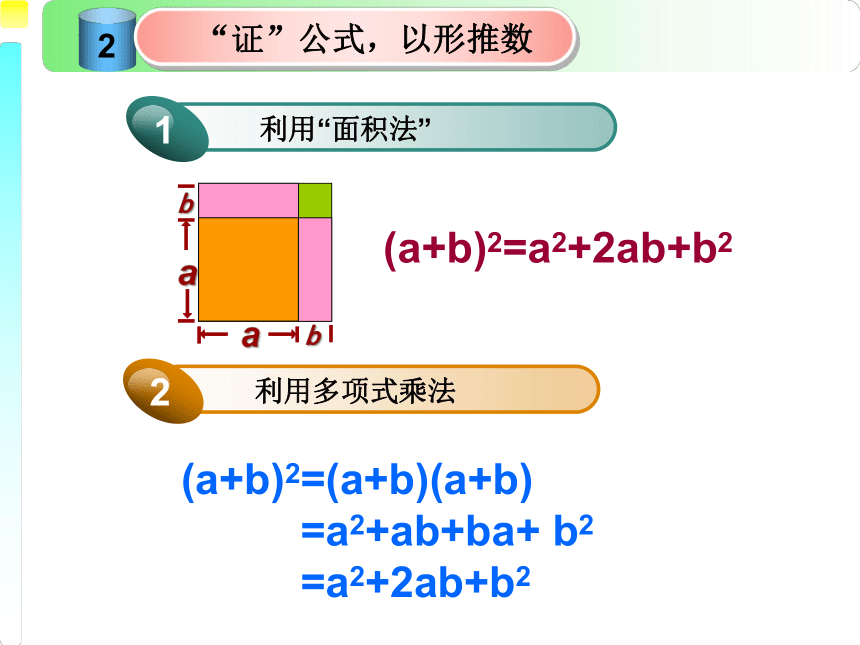
“证”公式,以形推数
(a+b)2=a2+2ab+b2
(a+b)2
ab
b2
ab
1
利用“面积法”
2
利用多项式乘法
(a+b)2=(a+b)(a+b)
=a2+ab+ba+ b2
=a2+2ab+b2
(a+b)2=a2+2ab+b2
a
b
b
a
2
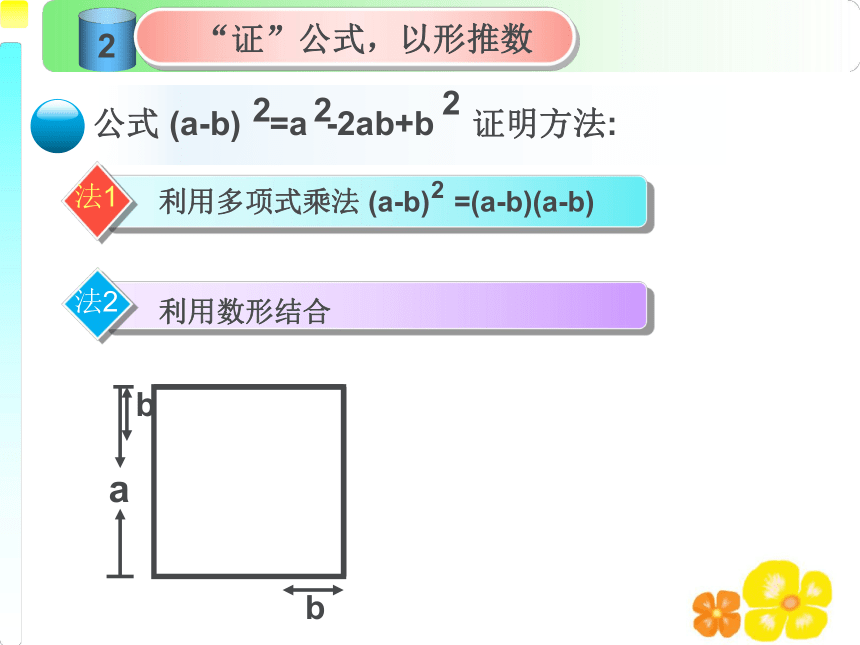
“证”公式,以形推数
2
2
2
合作交流,探求新知
公式 (a-b) =a -2ab+b 证明方法:
利用数形结合
法2
利用多项式乘法 (a-b) =(a-b)(a-b)
法1
2
http://cweihua.blog.
2
“证”公式,以形推数
a
b
b
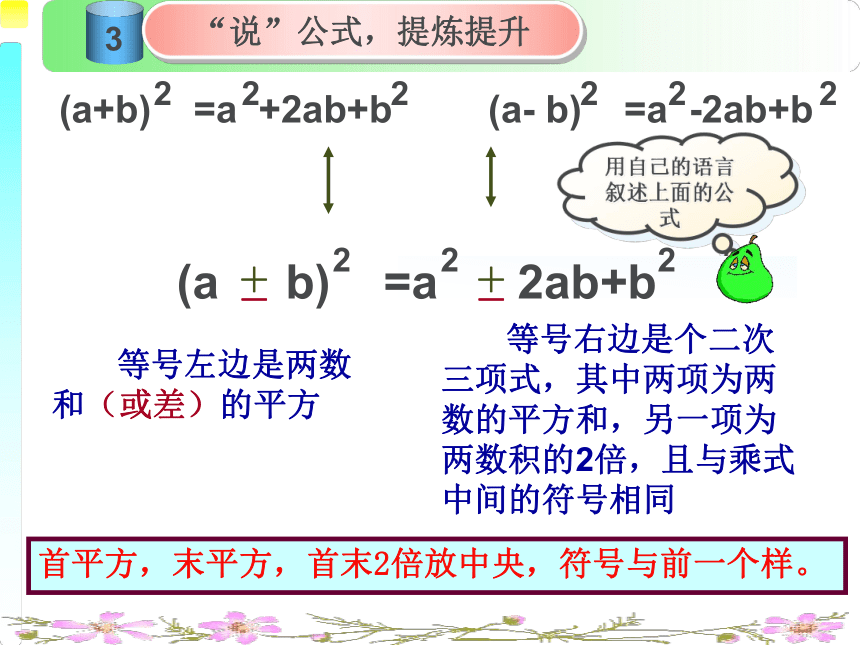
用自己的语言叙述上面的公式
(a+b) =a +2ab+b (a- b) =a -2ab+b
2
2
2
2
2
2
(a b) =a 2ab+b
-
+
-
+
2
2
2
http://cweihua.blog.
3
“说”公式,提炼提升
等号左边是两数和(或差)的平方
等号右边是个二次三项式,其中两项为两数的平方和,另一项为两数积的2倍,且与乘式中间的符号相同
首平方,末平方,首末2倍放中央,符号与前一个样。
解: (1) (5m+n)2=
例1 (1) (5m+n)2 (2) (3x-0.5)2
(a + b)2 = a2 + 2 ab + b2
(5m)2
+2 (5m) n
+n2
4
“练”公式,学以致用
让我们来做游戏
下面的计算中有些地方用纸牌盖上了,我们来比一比谁能最快地说出纸牌下盖的是什么式子。
(1)(3x+2y)2=9x2+12xy+4y2
(2)(5m-4n)2=25m2-40mn+16n2
(3)(4a+3b) 2=16a2+24ab+9b2
(4)(2x-8y)2=4x2-32xy+64y2
9x2
+16n2
+24ab
-32xy
随堂练习3分钟
运用完全平方公式计算:
判断等式是否成立 说明理由.
(1) ( a+1)2=(1 a)2
(2) ( a 1)2=(a+1)2
(3) (a 1)(1 a)=(a 1)2
(4) (a 1)( 1 a)=(a 1)(a+1)
成立
成立
不成立
不成立
深入探究
你来当老师
小明学习了完全平方公式以后,做了三道题,可他不知道自己做对了没有,请你帮小明检查一下。如果有错误,请你帮他改正。
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
例2:
(1) 1032 (2)982
解:(1) 原式 = ( 100 + 3)2
= 1002 + 2 ×100×3 + 32
= 10000 + 600 + 9
= 10609
(2)原式 = ( 100- 2)2
= 1002 - 2 × 100×2 + 22
= 10000 - 400 + 4
=9604
4
“练”公式,学以致用
速算比赛
(速算)个位数是5的两位数的平方
5
“拓”公式,挑战自我
(1)问: 等于多少?
(2)如果用10a+5表示个位数是5的这两位数,你能用所学的知识解释这个规律吗?
5
“拓”公式,挑战自我
本节课你学到了什么
完全平方公式
义务教育教科书八年级上册14.2.2
数缺形时少直观,
形少数时难入微。
数形结合百般好,
隔离分家万事非。
———华罗庚
小苏
小菲
1
谁买蛋糕更划算
通过这个图形,你能利用面积关系计算(a+b) 吗?
b
b
a
a
2
“证”公式,以形推数
(a+b)2=a2+2ab+b2
(a+b)2
ab
b2
ab
1
利用“面积法”
2
利用多项式乘法
(a+b)2=(a+b)(a+b)
=a2+ab+ba+ b2
=a2+2ab+b2
(a+b)2=a2+2ab+b2
a
b
b
a
2
“证”公式,以形推数
2
2
2
合作交流,探求新知
公式 (a-b) =a -2ab+b 证明方法:
利用数形结合
法2
利用多项式乘法 (a-b) =(a-b)(a-b)
法1
2
http://cweihua.blog.
2
“证”公式,以形推数
a
b
b
用自己的语言叙述上面的公式
(a+b) =a +2ab+b (a- b) =a -2ab+b
2
2
2
2
2
2
(a b) =a 2ab+b
-
+
-
+
2
2
2
http://cweihua.blog.
3
“说”公式,提炼提升
等号左边是两数和(或差)的平方
等号右边是个二次三项式,其中两项为两数的平方和,另一项为两数积的2倍,且与乘式中间的符号相同
首平方,末平方,首末2倍放中央,符号与前一个样。
解: (1) (5m+n)2=
例1 (1) (5m+n)2 (2) (3x-0.5)2
(a + b)2 = a2 + 2 ab + b2
(5m)2
+2 (5m) n
+n2
4
“练”公式,学以致用
让我们来做游戏
下面的计算中有些地方用纸牌盖上了,我们来比一比谁能最快地说出纸牌下盖的是什么式子。
(1)(3x+2y)2=9x2+12xy+4y2
(2)(5m-4n)2=25m2-40mn+16n2
(3)(4a+3b) 2=16a2+24ab+9b2
(4)(2x-8y)2=4x2-32xy+64y2
9x2
+16n2
+24ab
-32xy
随堂练习3分钟
运用完全平方公式计算:
判断等式是否成立 说明理由.
(1) ( a+1)2=(1 a)2
(2) ( a 1)2=(a+1)2
(3) (a 1)(1 a)=(a 1)2
(4) (a 1)( 1 a)=(a 1)(a+1)
成立
成立
不成立
不成立
深入探究
你来当老师
小明学习了完全平方公式以后,做了三道题,可他不知道自己做对了没有,请你帮小明检查一下。如果有错误,请你帮他改正。
(1) (2a 1)2=2a2 2a+1;
(2) (2a+1)2=4a2 +1;
(3) ( a 1)2= a2 2a 1.
例2:
(1) 1032 (2)982
解:(1) 原式 = ( 100 + 3)2
= 1002 + 2 ×100×3 + 32
= 10000 + 600 + 9
= 10609
(2)原式 = ( 100- 2)2
= 1002 - 2 × 100×2 + 22
= 10000 - 400 + 4
=9604
4
“练”公式,学以致用
速算比赛
(速算)个位数是5的两位数的平方
5
“拓”公式,挑战自我
(1)问: 等于多少?
(2)如果用10a+5表示个位数是5的这两位数,你能用所学的知识解释这个规律吗?
5
“拓”公式,挑战自我
本节课你学到了什么
