3.6指数函数、幂函数、对数函数增长的比较课件 北师大必修1
文档属性
| 名称 | 3.6指数函数、幂函数、对数函数增长的比较课件 北师大必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 90.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-18 15:29:44 | ||
图片预览

文档简介
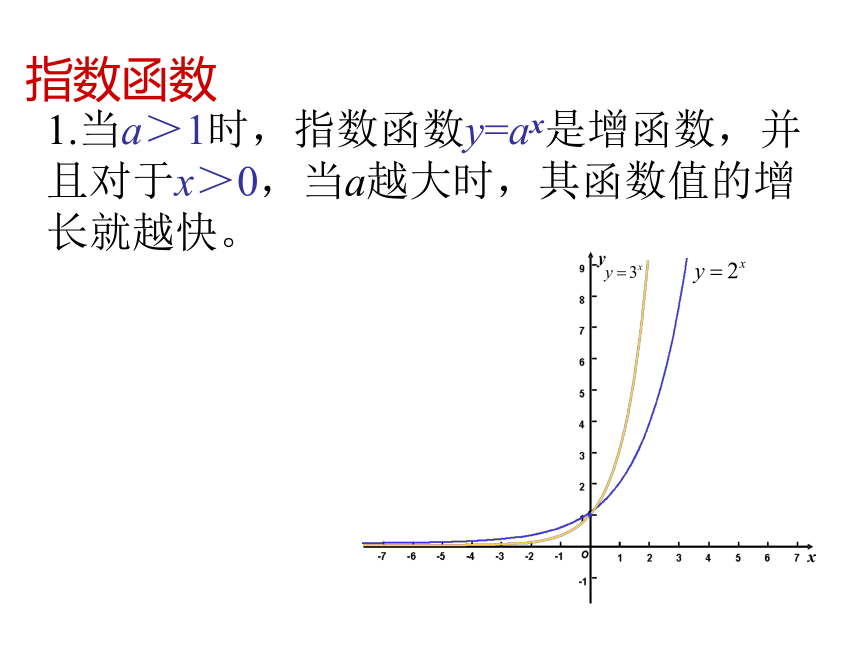
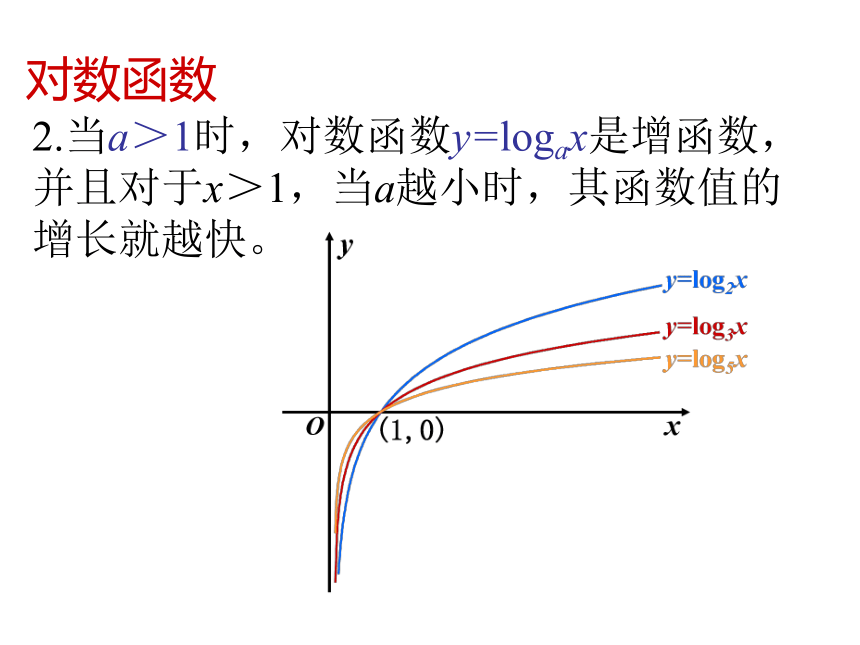
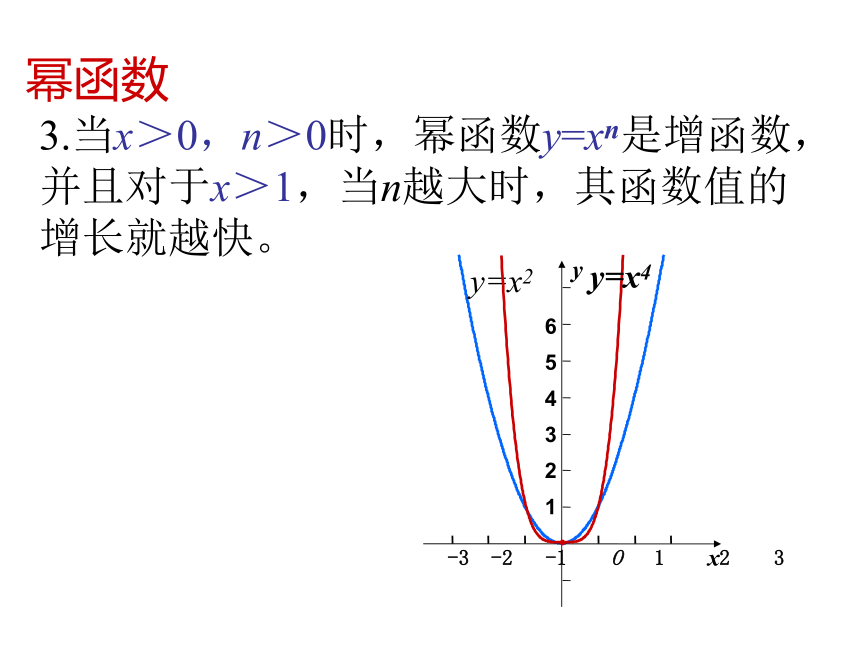
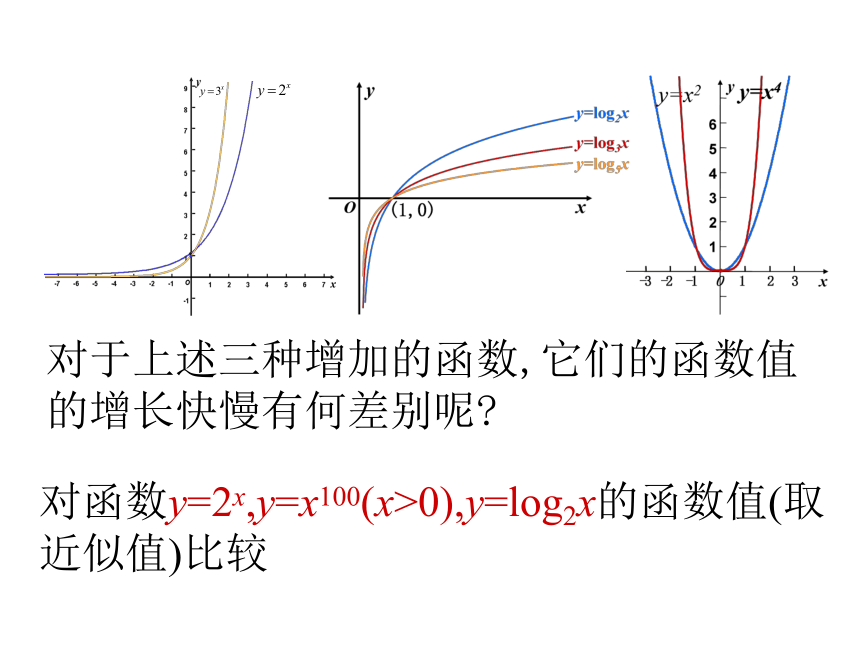
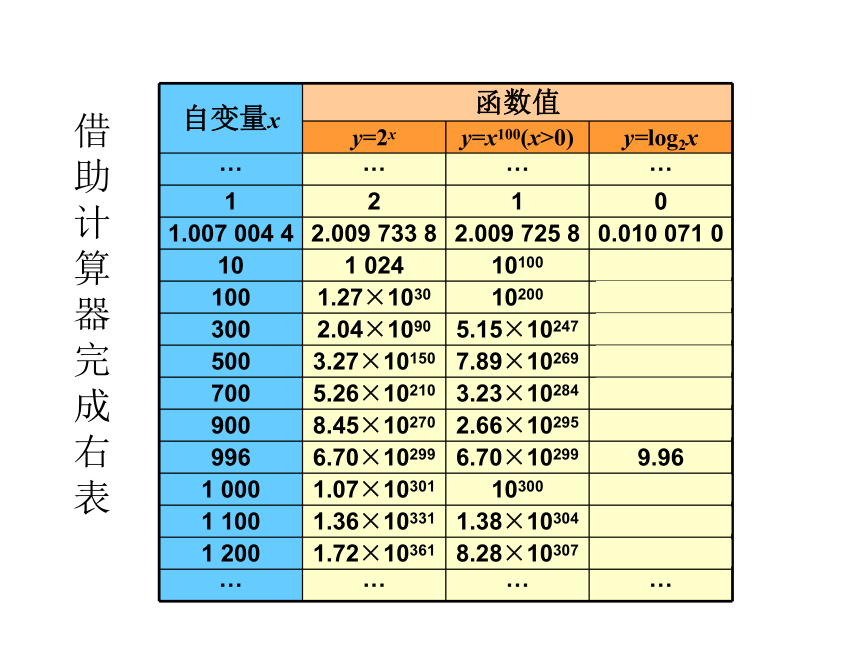
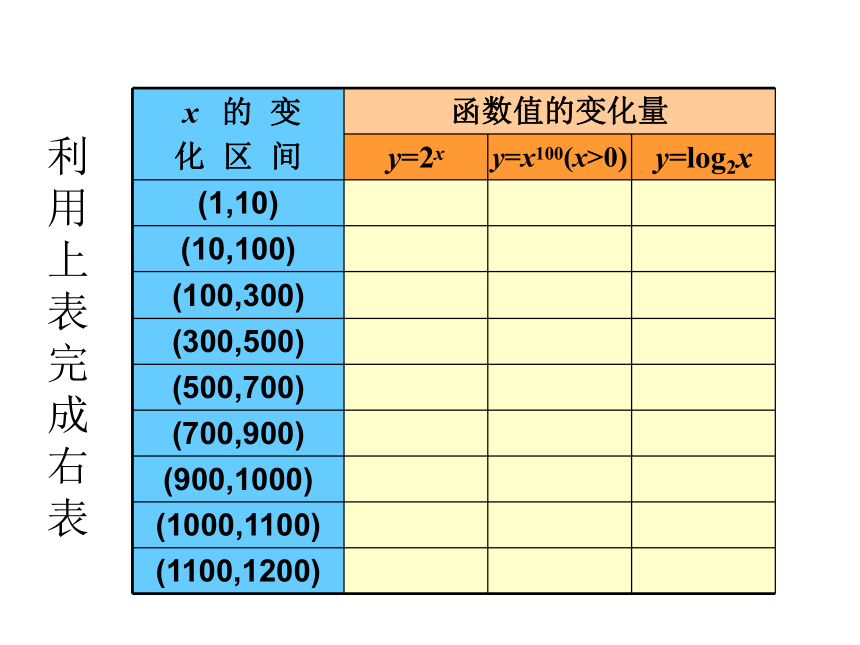
课件19张PPT。指数函数、幂函数、对数函数增长的比较1.当a>1时,指数函数y=ax是增函数,并且对于x>0,当a越大时,其函数值的增长就越快。指数函数2.当a>1时,对数函数y=logax是增函数,并且对于x>1,当a越小时,其函数值的增长就越快。对数函数3.当x>0,n>0时,幂函数y=xn是增函数,并且对于x>1,当n越大时,其函数值的增长就越快。幂函数对于上述三种增加的函数,它们的函数值的增长快慢有何差别呢?对函数y=2x,y=x100(x>0),y=log2x的函数值(取近似值)比较借助计算器完成右表利用上表完成右表4、谈函数y=2x,y=x100(x>0),y=log2x的函数值增长快慢的体会。
随着x的值越大
y=log2x的函数值增长的越来越慢,
y=2x和y=x100的函数值增长的 越来越快,
y=log2x增长比y=2x和y=x100要慢的多。
对函数y=2x和y=x100而言,
在x比较小时,会存在y=x100比y=2x的增长快的情况,
当x比较大时,y=2x比y=x100增长得更快。5、在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
因此,总会存在一个x0,
使得当x>x0时,一定有ax>xn>logax.指数函数值长非常快,因而常称这种现象为”指数爆炸”假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前 一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?令第x天,回报为y元
方案一: y=40
方案二: y=10x(x∈N+)
方案三: y=2x·0.4(x∈N+)分析投资5天以下选方案一
投资5-8天以下选方案二
投资8天以上选方案三某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加但奖金不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x
问:其中哪个模型能符合公司的要求?下面请大家作出这三个函数的图像,看图分析 对于模型y=0.25x,它在区间[10,1000]上是递增
当x?(20,1000)时,y>5,因此该模型不符合要求;对于模型由y=1.002x函数图像并利用计算器,可以知道在区间(805,806)内有一个点x0满足1.002x0=5,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,因此该模型也不符合要求;对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,
y=log71000+1≈4.55<5,所以它符合1、0.32,log20.3,20.3这三个数之间大小关系是( ) A. 0.32<20.3<log20.3;
B. 0.32<log20.3<20.3;
C. log20.3<20.3<0.32;
D. log20.3<0.32<20.3;D练习2、作图像,试比较函数y=4x,y=x4, y=log4x的增长情况.练习小结比较了指数函数、幂函数、对数函数的增长在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
随着x的值越大
y=log2x的函数值增长的越来越慢,
y=2x和y=x100的函数值增长的 越来越快,
y=log2x增长比y=2x和y=x100要慢的多。
对函数y=2x和y=x100而言,
在x比较小时,会存在y=x100比y=2x的增长快的情况,
当x比较大时,y=2x比y=x100增长得更快。5、在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
因此,总会存在一个x0,
使得当x>x0时,一定有ax>xn>logax.指数函数值长非常快,因而常称这种现象为”指数爆炸”假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前 一天多回报10元;
方案三:第一天回报0 .4元,以后每天的回报比前一天翻一番.
请问,你会选择哪种投资方案?令第x天,回报为y元
方案一: y=40
方案二: y=10x(x∈N+)
方案三: y=2x·0.4(x∈N+)分析投资5天以下选方案一
投资5-8天以下选方案二
投资8天以上选方案三某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加但奖金不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x
问:其中哪个模型能符合公司的要求?下面请大家作出这三个函数的图像,看图分析 对于模型y=0.25x,它在区间[10,1000]上是递增
当x?(20,1000)时,y>5,因此该模型不符合要求;对于模型由y=1.002x函数图像并利用计算器,可以知道在区间(805,806)内有一个点x0满足1.002x0=5,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,因此该模型也不符合要求;对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,
y=log71000+1≈4.55<5,所以它符合1、0.32,log20.3,20.3这三个数之间大小关系是( ) A. 0.32<20.3<log20.3;
B. 0.32<log20.3<20.3;
C. log20.3<20.3<0.32;
D. log20.3<0.32<20.3;D练习2、作图像,试比较函数y=4x,y=x4, y=log4x的增长情况.练习小结比较了指数函数、幂函数、对数函数的增长在区间(0,+∞)上,当a>1,n>0时,当x足够大时,随着x的增大,y=ax的增长速度越来越快,会超过并远远大于y=xn的增长速度,而y=logax的增长速度则越来越慢.
