湖北省随州市曾都区四校联考2023届九年级下学期5月月考数学试卷(pdf版含答案)
文档属性
| 名称 | 湖北省随州市曾都区四校联考2023届九年级下学期5月月考数学试卷(pdf版含答案) |  | |
| 格式 | |||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 13:01:35 | ||
图片预览




文档简介
2022-2023 学年度九年级五月考试试题
初中数学
考试时间:120分钟;分数:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题 (每小题 3 分,共 30分)
1.下列实数中,比 2小的是( )
5 3
A. B.0 C. D.1
2 2
2.如图,小明在做英语作业时,无意中把直角三角板放在了英文本上,他
用量角器测量出 1 38 ,则 2的度数是( )
第 2 题图
第 3 题图
A.128 B.138 C.142 D.152
3.为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来
自不同年级的 26 名参赛同学的得分情况如图所示,这些成绩的众数和中位
数分别是( )
A.98,98 B.98,97 C.96,98 D.96,96
4.如果一个几何体恰好可以无缝隙地以 3 个不同形状的“姿势”穿过如图所示
的“墙”上的 3 个空洞,则该几何体为( )
A. B. C. D
5.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一
牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马
价各几何. ”其大意为:现有两匹马加一头牛价钱超过一万,超过的部分正
好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是
半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为 x 元,一头牛
试卷第 1 页,共 6 页
价钱为 y 元,则符合题意的方程组是( )
x x
2x+y 10000 2x y 10000 2 2
A. B.
y y10000 (x 2y) x 2y 10000
2 2
x x
2x y 10000 2x y 10000 2 2
C. D.
y yx 2y 10000 1000 (x 2y)
2 2
6.2023 年 2 月 15 日,春运落下帷幕,在人流不息的画卷里,“流动的中国”
活力无限,交通运输部相关负责人表示,2023 年春运全社会人员流动量约
47.33 亿人次,比 2022 年同期增长 50.5%,将数据 47.33 亿用科学记数法表
示为( )
A.4.733 10 B.0.4733 102 C.4.733 108 D.4.733 109
7.如图,衣架可以近似看成一个等腰三角形 ABC,其中 AB AC, BAC 126 ,
BC 44cm,则高 AD约为( ).(参考数据:sin 27 0.45,cos27 0.89,
tan 27 0.51)
第 8 题图
第 7 题图
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
8.A、B 两地相距 4000 米,甲货车从 A 地匀速开往 B 地,乙货车在甲货车
出发 10 分钟后,从 B 地沿同一公路出发匀速开往 A 地,到达 A 地后停止,
而甲继续开往 B 地,到达 B 地后才停止.两车之间的距离 y(米)与甲货车
出发的时间 x(分钟)之间的函数关系如图中的折线CD—DE—EF —FG所
示:①甲的速度为 100 米/分钟;②乙的速度为 140 米/分钟;③乙货车从 B
80 1000
地到 A 地用的时间为 分钟;④当乙到达 A 地时,甲离 B 地的距离为
3 3
米.上述说法正确的是( )
A.①②③ B.①③④ C.①③ D.②④
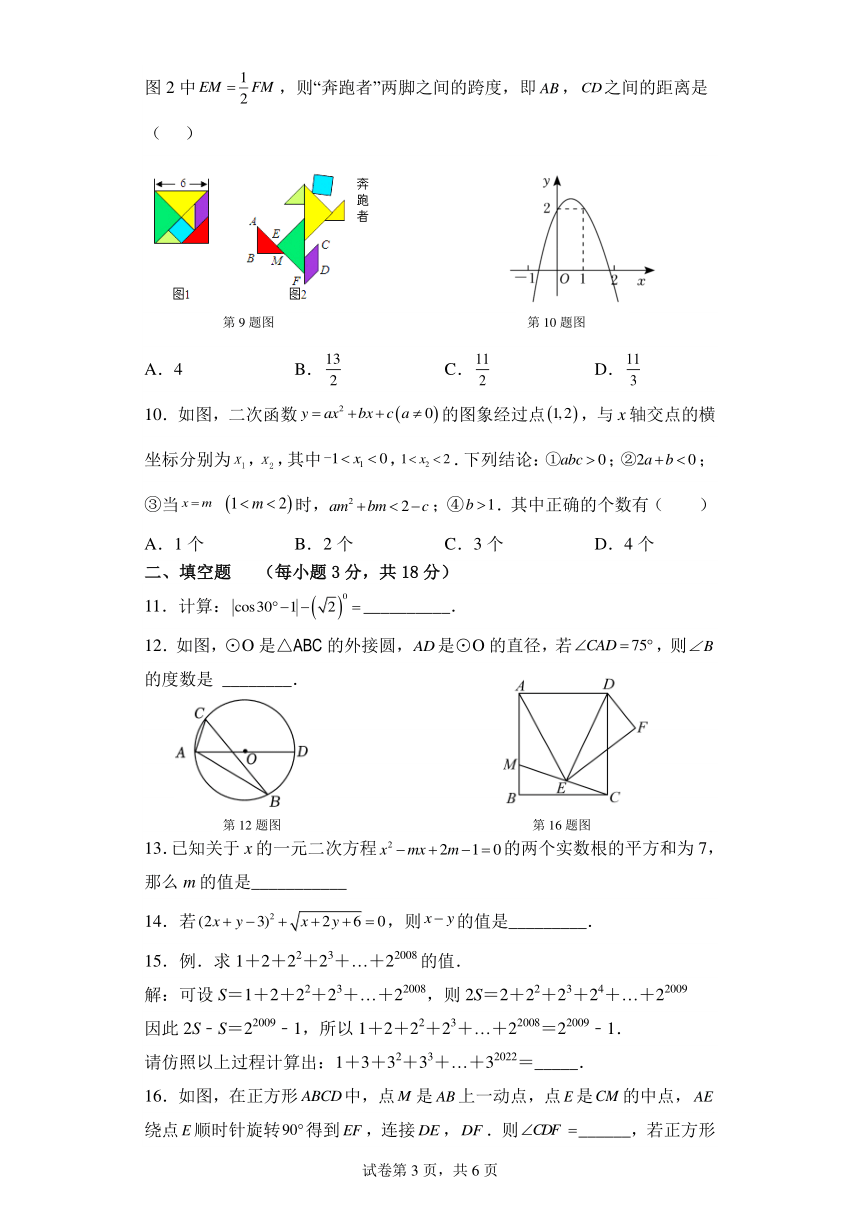
9.在数学“综合与实践”活动课上,小红同学用正方形纸片制作成图 1 所示的
七巧板,并拼成图 2 的“奔跑者”形象.已知图 1 中正方形纸片的边长为 6,
试卷第 2 页,共 6 页
1
图 2 中 EM FM ,则“奔跑者”两脚之间的跨度,即 AB,CD之间的距离是
2
( )
第 9 题图 第 10 题图
13 11 11
A.4 B. C. D.
2 2 3
2
10.如图,二次函数 y ax bx c a 0 的图象经过点 1,2 ,与 x 轴交点的横
坐标分别为x ,x ,其中-1 x1 0,1 x2 21 2 .下列结论:①abc 0;②2a b 0;
③当 x m 1 m 2 时,am2 bm 2 c;④b 1.其中正确的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题 (每小题 3分,共 18 分)
0
11.计算: cos30 1 2 __________.
12.如图,⊙O 是△ABC 的外接圆,AD是⊙O 的直径,若 CAD 75 ,则 B
的度数是 ________.
第 12 题图 第 16 题图
13.已知关于 x 的一元二次方程 x2 mx 2m 1 0的两个实数根的平方和为 7,
那么 m 的值是___________
14.若 (2x y 3)2 x 2y 6 0,则 x y的值是_________.
15.例.求 1+2+22+23+…+22008 的值.
解:可设 S=1+2+22+23+…+22008,则 2S=2+22+23+24+…+22009
因此 2S﹣S=22009﹣1,所以 1+2+22+23+…+22008=22009﹣1.
请仿照以上过程计算出:1+3+32+33+…+32022=_____.
16.如图,在正方形 ABCD中,点M 是 AB上一动点,点E是CM 的中点,AE
绕点 E顺时针旋转90 得到EF ,连接DE ,DF .则 CDF ______,若正方形
试卷第 3 页,共 6 页
ABCD的边长为 2,则点M 在射线 AB上运动时,CF 的最小值是______.
三、解答题
3x x x
17.(6 分)已知:A ,先化简 A,再从 1 x 2中取一个
x 1 x 1 x
2
1
合适的值代入,求 A 的值.
2
18.(7 分)如图,一次函数 y kx b(k 0)与反比例函数 y 的图象相交于
x
点 A 2,1 、B n, 2 两点.
(1)求一次函数的解析式;
(2)连接OA、OB,求△AOB 的面积:
2
(3)当 kx b 时,直接写出 x 的取值范围.
x
19.(8 分)已知:如图△ABC 中, B 90 , AB 3, BC 4,点D是BC边上一
点.
(1)尺规作图:以 AC 为对角线作平行四边形CDAE(要求:保留作图痕迹,不
写作法);
(2)填空:当 BD 时,平行四边形CDAE是菱形.
20.(10 分)随着移动互联网的迅猛发展,人们购物的支付方式更加多样、
便捷.某商场想了解顾客支付方式的选择情况,设计了一份问卷进行调查,
要求被调查者选择且只选择一种最喜欢的支付方式.现将调查结果绘制成如
图所示的两幅不完整的统计图.
试卷第 4 页,共 6 页
请结合图中所给出的信息,解答下列问题:
(1)扇形统计图中m ____________,“其他”支付方式所对应的圆心角为
______________度;
(2)补全条形统计图;
(3)若该商场一天内有 3000 次支付记录,请你估计选择现金支付的次数;
(4)甲乙两人到商场购物,如果四种支付方式选择的可能性一样,请用列表或
画树状图的方法,求出两人选择同一支付方式的概率.
21.(9 分)如图, AB为⊙O 的直径,点C 在⊙O 上,点 P 是直径 AB上的一
点(不与A , B 重合),过点 P 作 AB的垂线交BC的延长线于点Q.
(1)在线段 PQ 上取一点D,使 DQ=DC,连接DC ,求证:DC 是⊙O 的切线;
3
(2) cos B ,BP 6, AP 1,求 QC 的长.
5
22.(10 分)“美丽乡村”建设全面改善了农村环境面貌,吸引大量返乡人员
在家兴创业,某村结合本村优势成立了合作社,计划投资开展水产养殖和草
莓种植,根据市场调查与预测,水产养殖的利润 y1与投资量 x( x 0)成正
比例关系,如图 2 所示;草莓种植的利润 y2 与投资量 x成二次函数关系,如
图 1 所示(注:利润与投资量的单位都是万元).
(1)直 y y x.接.写.出.利润 1与 2 关于投资量 的函数关系式;
(2)如果该村合作社以 8 万元资金投入水产养殖和草莓种植,至少获得多少利
润?能获取的最大利润是多少?
(3)在(2)的基础上要保证获利不低于 22 万元,该村合作社至多应投资水产
试卷第 5 页,共 6 页
养殖多少万元?
23.(10 分)综合与探究
(1)如图 1,在正方形 ABCD中,点 E,F 分别在边BC,CD上,且 AE BF ,则
线段 AE与 BF 的之间的数量关系为______;
(2)【类比探究】如图 2,在矩形 ABCD中, AB 3, AD 5,点 E,F 分别在边
BC,CD上,且 AE BF ,请写出线段 AE与 BF 的数量关系,并证明你的结论.
(3)【拓展延伸】如图 3,在Rt△ABC 中, ABC 90 , AB 4,BC 6,D 为
BC上一点,且 BD 2,连接 AD,过点 B 作BE AD于点 F,交 AC 于点 E,
求 BE 的长.
24.(12 分)如图,抛物线 y ax2 bx 2 2(a 0)与 y 轴相交于点 C,且经过
A(1,0),B(4,0)两点,连接 AC .
(1)求抛物线的解析式;
(2)点 P 为抛物线在 x 轴下方图形上的一动点,是否存在点 P,使
1
PBO CAO ,若存在,求出点 P 坐标;若不存在,说明理由;
2
(3)若抛物线顶点为 M,对称轴与 x 轴的交点为 N,点 Q 为 x 轴上一动点,以
Q、M、N 为顶点的三角形与△AOC 相似.请直接写出点 Q 坐标.
试卷第 6 页,共 6 页
参考答案:
1.A 2.A 3.B 4.A 5.A
6.D 7.B 8.B 9.B 10.C
3 1
11. 或 3 12.15 /15 度 13. 1
2 2
32023 - 1
14.9 15.
2
16. 45度 2
【详解】解:如图 1 所示,延长 AE交DC 的延长线于点H ,
点 E是CM 的中点,
ME EC,
四边形 ABCD是正方形,
AB∥CD,
MAE H , AME HCE,
△AME≌△HCE(AAS),
AE EH ,
又 ADH 90 ,
DE AE EH,
AE 绕点 E顺时针旋转90 得到EF ,
AE EF , AEF 90 ,
AE DE EF ,
DAE ADE, EDF EFD,
AEF DAE ADE EDF EFD 360 ,
2 ADE 2 EDF 270 ,
答案第 1 页,共 11 页
ADF 135 ,
CDF ADF ADC 135 90 45 ;
如图 2 所示,连接 FC,过点C 作CF DF 于F ,
Q CDF 45 ,
点 F 在直线DF 上运动,
当CF ^ DF 时,CF 有最小值,最小值为CF 的长度,
CD 2, CDF 45 ,
2
CF 2 ,即CF 有最小值为 2 ,
2
故答案为: 45 , 2 .
17. 2x 4, A 8
3x x x
【详解】解: A
x 1 x 1 x
2 1
3x(x 1) x(x 1) (x 1)(x 1)
(x 1)(x 1) x
2x 4 -------4 分
1 x 2 ∵由题意得 x 1或 0 -----5 分
∴可取 x 2代入 2x 4,则 A 8.----6 分
18
2 2
【详解】(1)解:把 B n, 2 代入 y 得: 2 ,
x n
解得 n 1,
∴B 1, 2 ,
2k b 1
把 A 2,1 ,B 1, 2 分别代入 y kx b得 ,
k b 2
k 1
解得 ,
b 1
答案第 2 页,共 11 页
∴一次函数解析式为 y= x 1; -----3 分
(2)解:令 x 0,则 y 1,
∴直线 AB与 y 轴的交点C 0, 1 ,即OC 1,
1 1 3
∴ S△AOB OC xB xA 1 1 2 ; ----5 分
2 2 2
2
(3)解:由图象可知不等式 kx b 的解集为: x< 2或0 x 1. ---7 分
x
19
【详解】(1)解:以点A ,点C 为圆心,适当长为半径画弧交于两点,连接两点
交 AC 于点O,连接DO并延长,在延长线上截取OD OE,连接 AD, AE,CE,
如图所示,即为所求,
证明:由以点A ,点C 为圆心,适当长为半径,画弧交于两点,连接连点交 AC 于
点O,
可知,该直线为线段 AC 的垂直平分线,即:OC OA,
又∵OD OE,
∴四边形CDAE是平行四边形; -----4 分
(2)设 BD x,
∵BC 4,
答案第 3 页,共 11 页
∴CD 4 x,
∵平行四边形CDAE是菱形,
∴ AD CD 4 x,
∵ B 90 , AB 3,
2
则由勾股定理可得:BD2 AB2 AD2,即: x2 32 4 x ,
7
解得: x ,
8
7
故答案为: . -----8 分
8
20
60
【详解】(1) 200(人)
30%
50
m% 100% 25%
200
∴m 25,
30
“其他”支付方式所对应的圆心角为 360 54 ----2 分
200
故答案为: 25,54.
(2)补全条形统计图如图,
60 30% 200人,200 50 60 30 60人
补全条形统计图如图所示:
----4 分
(3)3000 30% 900,
答:估计选择现金支付的次数约为 900 次;----6 分
(4)解:画出树状图如图所示,
答案第 4 页,共 11 页
由树状图可知,共有 16 种结果,并且每一种结果出现的可能性相同,其中两人
恰好都选择同一支付方式的结果有 4 种,
所以两人恰好都选择微信支付的概率为1 ∕ 4。——(10 分)
21
【详解】(1)解:证明:连接OC ,如图,
QOC OB,
2 B,
DQ DC,
1 Q,
QP PB,
BPQ 90 ,
Q B 90 ,
1 2 90 ,
DCO 180 1 2 90 ,
OC CD,
而OC 为 O的半径,
CD为 O的切线; ----4 分
(2)连接 AC ,如图,
AB为 O的直径,
答案第 5 页,共 11 页
ACB 90 ,
BC BC 3
在Rt△ABC 中, cos B ,
AB AP PB 5
而BP 6, AP 1,
21
BC ,
5
PB 3
在Rt BPQ中, cos B ,
BQ 5
6
BQ 10
3 ,
5
21 29
QC BQ BC 10 .----9 分
5 5
22. 【详解】(1)解:设 y kx,y ax21 2 ,
把P 1,2 代入 y1 kx中得: k 2; -----1 分
1
把Q 2,2 代入 y ax22 中得:2 4a,解得 a ; ----2 分
2
1
∴ y1 2x x 0 ,y2 x
2 x 0 ------3 分
2
(2)解:设投入水产养殖的资金为 m 万元,则投入草莓种植的资金为 8 m 万
元,总利润为 W万元,
1 2
由题意得,W 2m 8 m
2
1
m2 16m 64 2m
2
1
m2 12m 64
2
1 2
m 6 14,
2
1
∵ 0,0 m 8,
2
∴当m 6时,W最小,最小值为 14,
∴至少获得 14 万元的利润;
1 2 1 2
当m 0时,W 0 6 14 32,当m 8时,W 8 6 14 16,
2 2
∵32 16,
∴当m 0时,W最大,最大为 32,
答案第 6 页,共 11 页
∴能获取的最大利润是 32 万元; ---------7 分
1 2
(3)解:当W 22时,则 m 6 14 22,
2
解得m 2或m 10(舍去),
∴要保证获利不低于 22 万元,则m 2,
∴投入水产养殖的资金至多为 2 万元.----10 分
23
【详解】(1)解:设 AE与 BF 相交于点 P ,如图,
∵正方形 ABCD,
∴ ABC C 90 , AB BC,
∵ AE BF ,
∴ APB BAP ABP 90 ,
∵ ABP CBF 90 ,
∴ BAP CBF ,
在 ABE和△BCF 中,
BAE CBF
AB CB ,
ABE BCF
∴△ABE≌△BCF ASA ,
∴ AE BF;
故答案为: AE BF;-------3 分
AE 3
(2)解: .
BF 5
证明:∵ AE BF ,
∴ BAE ABF 90 .
答案第 7 页,共 11 页
在矩形 ABCD 中, ABC 90 ,
∴ CBF ABF 90 ,
∴ BAE CBF,
∴Rt ABE∽Rt BCF ,
AB AE
∴ ,
BC BF
AE 3
∴ .-----------6 分
BF 5
(3)解:如图,过点A 作 AB的垂线,过点C 作BC的垂线,两垂线交于点G ,延
长 BE 交CG 于点H .
∴四边形 ABCG是矩形.
∵ AB CD 4, AG BC 6,
∴CD 6 BD 4.
∴ AD AB2 BD2 2 5.
AD AB 2
由(2)知 ,
BH BC 3
∴BH 3 5 .
在Rt△BCH 中,CH BH 2 BC2 3,
∵ AB∥CH
∴ ABE∽ CHE,
AB BE
∴ ,
CH EH
4 BE
即 ,
3 3 5 BE
12 5
解得 BE . --------10 分
7
24
答案第 8 页,共 11 页
0 a b 2 2
【详解】(1)解:将 A(1,0),B(4,0)代入 y ax2 bx 2 2得, ,
0 16a 4b 2 2
2
a
2
解得 ,
5 2
b
2
2 2 5 2∴ y x x 2 2 ,
2 2
2
∴抛物线的解析式为 y x2
5 2
x 2 2 ; ------3 分
2 2
(2)解:如图 1,作 BE 交 y 轴于E,使 OBE 2 PBO CAO,延长BP交 y 轴
于 F ,过 F 作FG BE 于G ,
当 x 0, y 2 2 ,
∴C 0,2 2 ,OC 2 2
∵ COA EOB 90 , CAO OBE,
∴△AOC∽△BOE,
OC AO 2 2 1
∴ ,即 ,
OE BO OE 4
解得OE 8 2 ,
在Rt BOE中,由勾股定理得BE OB2 OE2 12,
∵ OBE 2 PBO,
∴ BP为 OBE的平分线,
∴FG OF,
设FG OF x,
答案第 9 页,共 11 页
1 1 1
∴ S BOE S OBF S BEF ,即 OB OE OB OF BE FG ,
2 2 2
1 1 1
∴ 4 8 2 4 x 12 x,
2 2 2
解得 x 2 2,
∴F 0, 2 2 ,
0 4m n
设直线 BF 的解析式为 y mx n,将B,F 代入得 ,
2 2 n
2
m
解得 2 ,
n 2 2
2
∴直线 BF 的解析式为 y x 2 2 ,
2
2
y x 2 2
2
联立 ,
2 2 5 2y x x 2 2
2 2
x1 2 x2 4
解得 , ,
y 2 y2 01
∴P 2, 2 ; ---------7 分
5
(3)解:由题意知,抛物线的对称轴为直线 x ,
2
5 9
当 x , y 2 ,
2 8
5 9 5 9
∴M , 2 ,N ,0 ,MN 2,
2 8 2 8
∵以 Q、M、N 为顶点的三角形与 AOC相似,且 AOC QNM 90 ,
∴分 AOC∽ QNM , AOC∽ MNQ两种情况求解;
5
设Q c,0 ,则QN c ,
2
AO OC 1 2 2
①当 AOC∽ QNM 时, ,即 9 ,
QN MN QN 2
8
9
解得QN ,
16
5 9
∴ c ,
2 16
答案第 10 页,共 11 页
49 31
解得 c1 , c2 ,
16 16
49 31
∴此时的Q点坐标为 ,0 或 ,0 ;
16 16
AO OC 1 2 2
②当 AOC∽ MNQ时, ,即 9 QN , MN QN 2
8
9
解得QN ,
2
5 9
∴ c ,
2 2
解得 c3 7, c4 2,
∴此时的Q点坐标为 7,0 或 2,0 ;
49 31
综上所述,Q点坐标为 ,0 或 ,0 或 7,0 或 2,0 .--------12 分
16 16
答案第 11 页,共 11 页
初中数学
考试时间:120分钟;分数:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题 (每小题 3 分,共 30分)
1.下列实数中,比 2小的是( )
5 3
A. B.0 C. D.1
2 2
2.如图,小明在做英语作业时,无意中把直角三角板放在了英文本上,他
用量角器测量出 1 38 ,则 2的度数是( )
第 2 题图
第 3 题图
A.128 B.138 C.142 D.152
3.为了增强学生预防新冠肺炎的安全意识,某校开展疫情防控知识竞赛.来
自不同年级的 26 名参赛同学的得分情况如图所示,这些成绩的众数和中位
数分别是( )
A.98,98 B.98,97 C.96,98 D.96,96
4.如果一个几何体恰好可以无缝隙地以 3 个不同形状的“姿势”穿过如图所示
的“墙”上的 3 个空洞,则该几何体为( )
A. B. C. D
5.我国古代数学著作《九章算术》记载了一道“牛马问题”:“今有二马、一
牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.问牛、马
价各几何. ”其大意为:现有两匹马加一头牛价钱超过一万,超过的部分正
好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是
半头牛的价钱,求一匹马、一头牛各多少钱?设一匹马价钱为 x 元,一头牛
试卷第 1 页,共 6 页
价钱为 y 元,则符合题意的方程组是( )
x x
2x+y 10000 2x y 10000 2 2
A. B.
y y10000 (x 2y) x 2y 10000
2 2
x x
2x y 10000 2x y 10000 2 2
C. D.
y yx 2y 10000 1000 (x 2y)
2 2
6.2023 年 2 月 15 日,春运落下帷幕,在人流不息的画卷里,“流动的中国”
活力无限,交通运输部相关负责人表示,2023 年春运全社会人员流动量约
47.33 亿人次,比 2022 年同期增长 50.5%,将数据 47.33 亿用科学记数法表
示为( )
A.4.733 10 B.0.4733 102 C.4.733 108 D.4.733 109
7.如图,衣架可以近似看成一个等腰三角形 ABC,其中 AB AC, BAC 126 ,
BC 44cm,则高 AD约为( ).(参考数据:sin 27 0.45,cos27 0.89,
tan 27 0.51)
第 8 题图
第 7 题图
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
8.A、B 两地相距 4000 米,甲货车从 A 地匀速开往 B 地,乙货车在甲货车
出发 10 分钟后,从 B 地沿同一公路出发匀速开往 A 地,到达 A 地后停止,
而甲继续开往 B 地,到达 B 地后才停止.两车之间的距离 y(米)与甲货车
出发的时间 x(分钟)之间的函数关系如图中的折线CD—DE—EF —FG所
示:①甲的速度为 100 米/分钟;②乙的速度为 140 米/分钟;③乙货车从 B
80 1000
地到 A 地用的时间为 分钟;④当乙到达 A 地时,甲离 B 地的距离为
3 3
米.上述说法正确的是( )
A.①②③ B.①③④ C.①③ D.②④
9.在数学“综合与实践”活动课上,小红同学用正方形纸片制作成图 1 所示的
七巧板,并拼成图 2 的“奔跑者”形象.已知图 1 中正方形纸片的边长为 6,
试卷第 2 页,共 6 页
1
图 2 中 EM FM ,则“奔跑者”两脚之间的跨度,即 AB,CD之间的距离是
2
( )
第 9 题图 第 10 题图
13 11 11
A.4 B. C. D.
2 2 3
2
10.如图,二次函数 y ax bx c a 0 的图象经过点 1,2 ,与 x 轴交点的横
坐标分别为x ,x ,其中-1 x1 0,1 x2 21 2 .下列结论:①abc 0;②2a b 0;
③当 x m 1 m 2 时,am2 bm 2 c;④b 1.其中正确的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题 (每小题 3分,共 18 分)
0
11.计算: cos30 1 2 __________.
12.如图,⊙O 是△ABC 的外接圆,AD是⊙O 的直径,若 CAD 75 ,则 B
的度数是 ________.
第 12 题图 第 16 题图
13.已知关于 x 的一元二次方程 x2 mx 2m 1 0的两个实数根的平方和为 7,
那么 m 的值是___________
14.若 (2x y 3)2 x 2y 6 0,则 x y的值是_________.
15.例.求 1+2+22+23+…+22008 的值.
解:可设 S=1+2+22+23+…+22008,则 2S=2+22+23+24+…+22009
因此 2S﹣S=22009﹣1,所以 1+2+22+23+…+22008=22009﹣1.
请仿照以上过程计算出:1+3+32+33+…+32022=_____.
16.如图,在正方形 ABCD中,点M 是 AB上一动点,点E是CM 的中点,AE
绕点 E顺时针旋转90 得到EF ,连接DE ,DF .则 CDF ______,若正方形
试卷第 3 页,共 6 页
ABCD的边长为 2,则点M 在射线 AB上运动时,CF 的最小值是______.
三、解答题
3x x x
17.(6 分)已知:A ,先化简 A,再从 1 x 2中取一个
x 1 x 1 x
2
1
合适的值代入,求 A 的值.
2
18.(7 分)如图,一次函数 y kx b(k 0)与反比例函数 y 的图象相交于
x
点 A 2,1 、B n, 2 两点.
(1)求一次函数的解析式;
(2)连接OA、OB,求△AOB 的面积:
2
(3)当 kx b 时,直接写出 x 的取值范围.
x
19.(8 分)已知:如图△ABC 中, B 90 , AB 3, BC 4,点D是BC边上一
点.
(1)尺规作图:以 AC 为对角线作平行四边形CDAE(要求:保留作图痕迹,不
写作法);
(2)填空:当 BD 时,平行四边形CDAE是菱形.
20.(10 分)随着移动互联网的迅猛发展,人们购物的支付方式更加多样、
便捷.某商场想了解顾客支付方式的选择情况,设计了一份问卷进行调查,
要求被调查者选择且只选择一种最喜欢的支付方式.现将调查结果绘制成如
图所示的两幅不完整的统计图.
试卷第 4 页,共 6 页
请结合图中所给出的信息,解答下列问题:
(1)扇形统计图中m ____________,“其他”支付方式所对应的圆心角为
______________度;
(2)补全条形统计图;
(3)若该商场一天内有 3000 次支付记录,请你估计选择现金支付的次数;
(4)甲乙两人到商场购物,如果四种支付方式选择的可能性一样,请用列表或
画树状图的方法,求出两人选择同一支付方式的概率.
21.(9 分)如图, AB为⊙O 的直径,点C 在⊙O 上,点 P 是直径 AB上的一
点(不与A , B 重合),过点 P 作 AB的垂线交BC的延长线于点Q.
(1)在线段 PQ 上取一点D,使 DQ=DC,连接DC ,求证:DC 是⊙O 的切线;
3
(2) cos B ,BP 6, AP 1,求 QC 的长.
5
22.(10 分)“美丽乡村”建设全面改善了农村环境面貌,吸引大量返乡人员
在家兴创业,某村结合本村优势成立了合作社,计划投资开展水产养殖和草
莓种植,根据市场调查与预测,水产养殖的利润 y1与投资量 x( x 0)成正
比例关系,如图 2 所示;草莓种植的利润 y2 与投资量 x成二次函数关系,如
图 1 所示(注:利润与投资量的单位都是万元).
(1)直 y y x.接.写.出.利润 1与 2 关于投资量 的函数关系式;
(2)如果该村合作社以 8 万元资金投入水产养殖和草莓种植,至少获得多少利
润?能获取的最大利润是多少?
(3)在(2)的基础上要保证获利不低于 22 万元,该村合作社至多应投资水产
试卷第 5 页,共 6 页
养殖多少万元?
23.(10 分)综合与探究
(1)如图 1,在正方形 ABCD中,点 E,F 分别在边BC,CD上,且 AE BF ,则
线段 AE与 BF 的之间的数量关系为______;
(2)【类比探究】如图 2,在矩形 ABCD中, AB 3, AD 5,点 E,F 分别在边
BC,CD上,且 AE BF ,请写出线段 AE与 BF 的数量关系,并证明你的结论.
(3)【拓展延伸】如图 3,在Rt△ABC 中, ABC 90 , AB 4,BC 6,D 为
BC上一点,且 BD 2,连接 AD,过点 B 作BE AD于点 F,交 AC 于点 E,
求 BE 的长.
24.(12 分)如图,抛物线 y ax2 bx 2 2(a 0)与 y 轴相交于点 C,且经过
A(1,0),B(4,0)两点,连接 AC .
(1)求抛物线的解析式;
(2)点 P 为抛物线在 x 轴下方图形上的一动点,是否存在点 P,使
1
PBO CAO ,若存在,求出点 P 坐标;若不存在,说明理由;
2
(3)若抛物线顶点为 M,对称轴与 x 轴的交点为 N,点 Q 为 x 轴上一动点,以
Q、M、N 为顶点的三角形与△AOC 相似.请直接写出点 Q 坐标.
试卷第 6 页,共 6 页
参考答案:
1.A 2.A 3.B 4.A 5.A
6.D 7.B 8.B 9.B 10.C
3 1
11. 或 3 12.15 /15 度 13. 1
2 2
32023 - 1
14.9 15.
2
16. 45度 2
【详解】解:如图 1 所示,延长 AE交DC 的延长线于点H ,
点 E是CM 的中点,
ME EC,
四边形 ABCD是正方形,
AB∥CD,
MAE H , AME HCE,
△AME≌△HCE(AAS),
AE EH ,
又 ADH 90 ,
DE AE EH,
AE 绕点 E顺时针旋转90 得到EF ,
AE EF , AEF 90 ,
AE DE EF ,
DAE ADE, EDF EFD,
AEF DAE ADE EDF EFD 360 ,
2 ADE 2 EDF 270 ,
答案第 1 页,共 11 页
ADF 135 ,
CDF ADF ADC 135 90 45 ;
如图 2 所示,连接 FC,过点C 作CF DF 于F ,
Q CDF 45 ,
点 F 在直线DF 上运动,
当CF ^ DF 时,CF 有最小值,最小值为CF 的长度,
CD 2, CDF 45 ,
2
CF 2 ,即CF 有最小值为 2 ,
2
故答案为: 45 , 2 .
17. 2x 4, A 8
3x x x
【详解】解: A
x 1 x 1 x
2 1
3x(x 1) x(x 1) (x 1)(x 1)
(x 1)(x 1) x
2x 4 -------4 分
1 x 2 ∵由题意得 x 1或 0 -----5 分
∴可取 x 2代入 2x 4,则 A 8.----6 分
18
2 2
【详解】(1)解:把 B n, 2 代入 y 得: 2 ,
x n
解得 n 1,
∴B 1, 2 ,
2k b 1
把 A 2,1 ,B 1, 2 分别代入 y kx b得 ,
k b 2
k 1
解得 ,
b 1
答案第 2 页,共 11 页
∴一次函数解析式为 y= x 1; -----3 分
(2)解:令 x 0,则 y 1,
∴直线 AB与 y 轴的交点C 0, 1 ,即OC 1,
1 1 3
∴ S△AOB OC xB xA 1 1 2 ; ----5 分
2 2 2
2
(3)解:由图象可知不等式 kx b 的解集为: x< 2或0 x 1. ---7 分
x
19
【详解】(1)解:以点A ,点C 为圆心,适当长为半径画弧交于两点,连接两点
交 AC 于点O,连接DO并延长,在延长线上截取OD OE,连接 AD, AE,CE,
如图所示,即为所求,
证明:由以点A ,点C 为圆心,适当长为半径,画弧交于两点,连接连点交 AC 于
点O,
可知,该直线为线段 AC 的垂直平分线,即:OC OA,
又∵OD OE,
∴四边形CDAE是平行四边形; -----4 分
(2)设 BD x,
∵BC 4,
答案第 3 页,共 11 页
∴CD 4 x,
∵平行四边形CDAE是菱形,
∴ AD CD 4 x,
∵ B 90 , AB 3,
2
则由勾股定理可得:BD2 AB2 AD2,即: x2 32 4 x ,
7
解得: x ,
8
7
故答案为: . -----8 分
8
20
60
【详解】(1) 200(人)
30%
50
m% 100% 25%
200
∴m 25,
30
“其他”支付方式所对应的圆心角为 360 54 ----2 分
200
故答案为: 25,54.
(2)补全条形统计图如图,
60 30% 200人,200 50 60 30 60人
补全条形统计图如图所示:
----4 分
(3)3000 30% 900,
答:估计选择现金支付的次数约为 900 次;----6 分
(4)解:画出树状图如图所示,
答案第 4 页,共 11 页
由树状图可知,共有 16 种结果,并且每一种结果出现的可能性相同,其中两人
恰好都选择同一支付方式的结果有 4 种,
所以两人恰好都选择微信支付的概率为1 ∕ 4。——(10 分)
21
【详解】(1)解:证明:连接OC ,如图,
QOC OB,
2 B,
DQ DC,
1 Q,
QP PB,
BPQ 90 ,
Q B 90 ,
1 2 90 ,
DCO 180 1 2 90 ,
OC CD,
而OC 为 O的半径,
CD为 O的切线; ----4 分
(2)连接 AC ,如图,
AB为 O的直径,
答案第 5 页,共 11 页
ACB 90 ,
BC BC 3
在Rt△ABC 中, cos B ,
AB AP PB 5
而BP 6, AP 1,
21
BC ,
5
PB 3
在Rt BPQ中, cos B ,
BQ 5
6
BQ 10
3 ,
5
21 29
QC BQ BC 10 .----9 分
5 5
22. 【详解】(1)解:设 y kx,y ax21 2 ,
把P 1,2 代入 y1 kx中得: k 2; -----1 分
1
把Q 2,2 代入 y ax22 中得:2 4a,解得 a ; ----2 分
2
1
∴ y1 2x x 0 ,y2 x
2 x 0 ------3 分
2
(2)解:设投入水产养殖的资金为 m 万元,则投入草莓种植的资金为 8 m 万
元,总利润为 W万元,
1 2
由题意得,W 2m 8 m
2
1
m2 16m 64 2m
2
1
m2 12m 64
2
1 2
m 6 14,
2
1
∵ 0,0 m 8,
2
∴当m 6时,W最小,最小值为 14,
∴至少获得 14 万元的利润;
1 2 1 2
当m 0时,W 0 6 14 32,当m 8时,W 8 6 14 16,
2 2
∵32 16,
∴当m 0时,W最大,最大为 32,
答案第 6 页,共 11 页
∴能获取的最大利润是 32 万元; ---------7 分
1 2
(3)解:当W 22时,则 m 6 14 22,
2
解得m 2或m 10(舍去),
∴要保证获利不低于 22 万元,则m 2,
∴投入水产养殖的资金至多为 2 万元.----10 分
23
【详解】(1)解:设 AE与 BF 相交于点 P ,如图,
∵正方形 ABCD,
∴ ABC C 90 , AB BC,
∵ AE BF ,
∴ APB BAP ABP 90 ,
∵ ABP CBF 90 ,
∴ BAP CBF ,
在 ABE和△BCF 中,
BAE CBF
AB CB ,
ABE BCF
∴△ABE≌△BCF ASA ,
∴ AE BF;
故答案为: AE BF;-------3 分
AE 3
(2)解: .
BF 5
证明:∵ AE BF ,
∴ BAE ABF 90 .
答案第 7 页,共 11 页
在矩形 ABCD 中, ABC 90 ,
∴ CBF ABF 90 ,
∴ BAE CBF,
∴Rt ABE∽Rt BCF ,
AB AE
∴ ,
BC BF
AE 3
∴ .-----------6 分
BF 5
(3)解:如图,过点A 作 AB的垂线,过点C 作BC的垂线,两垂线交于点G ,延
长 BE 交CG 于点H .
∴四边形 ABCG是矩形.
∵ AB CD 4, AG BC 6,
∴CD 6 BD 4.
∴ AD AB2 BD2 2 5.
AD AB 2
由(2)知 ,
BH BC 3
∴BH 3 5 .
在Rt△BCH 中,CH BH 2 BC2 3,
∵ AB∥CH
∴ ABE∽ CHE,
AB BE
∴ ,
CH EH
4 BE
即 ,
3 3 5 BE
12 5
解得 BE . --------10 分
7
24
答案第 8 页,共 11 页
0 a b 2 2
【详解】(1)解:将 A(1,0),B(4,0)代入 y ax2 bx 2 2得, ,
0 16a 4b 2 2
2
a
2
解得 ,
5 2
b
2
2 2 5 2∴ y x x 2 2 ,
2 2
2
∴抛物线的解析式为 y x2
5 2
x 2 2 ; ------3 分
2 2
(2)解:如图 1,作 BE 交 y 轴于E,使 OBE 2 PBO CAO,延长BP交 y 轴
于 F ,过 F 作FG BE 于G ,
当 x 0, y 2 2 ,
∴C 0,2 2 ,OC 2 2
∵ COA EOB 90 , CAO OBE,
∴△AOC∽△BOE,
OC AO 2 2 1
∴ ,即 ,
OE BO OE 4
解得OE 8 2 ,
在Rt BOE中,由勾股定理得BE OB2 OE2 12,
∵ OBE 2 PBO,
∴ BP为 OBE的平分线,
∴FG OF,
设FG OF x,
答案第 9 页,共 11 页
1 1 1
∴ S BOE S OBF S BEF ,即 OB OE OB OF BE FG ,
2 2 2
1 1 1
∴ 4 8 2 4 x 12 x,
2 2 2
解得 x 2 2,
∴F 0, 2 2 ,
0 4m n
设直线 BF 的解析式为 y mx n,将B,F 代入得 ,
2 2 n
2
m
解得 2 ,
n 2 2
2
∴直线 BF 的解析式为 y x 2 2 ,
2
2
y x 2 2
2
联立 ,
2 2 5 2y x x 2 2
2 2
x1 2 x2 4
解得 , ,
y 2 y2 01
∴P 2, 2 ; ---------7 分
5
(3)解:由题意知,抛物线的对称轴为直线 x ,
2
5 9
当 x , y 2 ,
2 8
5 9 5 9
∴M , 2 ,N ,0 ,MN 2,
2 8 2 8
∵以 Q、M、N 为顶点的三角形与 AOC相似,且 AOC QNM 90 ,
∴分 AOC∽ QNM , AOC∽ MNQ两种情况求解;
5
设Q c,0 ,则QN c ,
2
AO OC 1 2 2
①当 AOC∽ QNM 时, ,即 9 ,
QN MN QN 2
8
9
解得QN ,
16
5 9
∴ c ,
2 16
答案第 10 页,共 11 页
49 31
解得 c1 , c2 ,
16 16
49 31
∴此时的Q点坐标为 ,0 或 ,0 ;
16 16
AO OC 1 2 2
②当 AOC∽ MNQ时, ,即 9 QN , MN QN 2
8
9
解得QN ,
2
5 9
∴ c ,
2 2
解得 c3 7, c4 2,
∴此时的Q点坐标为 7,0 或 2,0 ;
49 31
综上所述,Q点坐标为 ,0 或 ,0 或 7,0 或 2,0 .--------12 分
16 16
答案第 11 页,共 11 页
同课章节目录
