3.5对数函数课件 北师大必修1

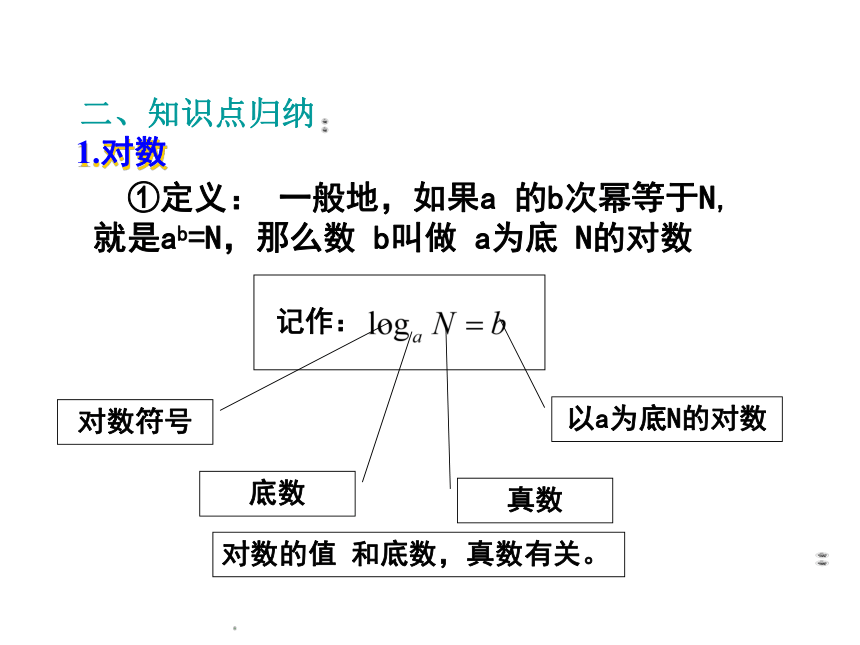
课件19张PPT。对数函数1.理解对数的概念，掌握对数的运算性质；2.掌握对数函数的概念、图像和性质. 能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题. 一、高考要求 ①定义： 一般地，如果a 的b次幂等于N,
就是ab=N，那么数 b叫做 a为底 N的对数 对数符号底数真数以a为底N的对数对数的值 和底数，真数有关。1.对数⑴ 负数与零没有对数 ③对数运算性质 ②对数性质 关系式 :logaN=b ab=N;④对数的换底公式 ⑤常用对数lgN,自然对数lnN 在(0,+∞)上是减函数在(0,+∞)上是增函数单调性（1，0）（1，0）过定点00
x>1时，y<00 x>1时，y>0函数值变化情况R R值 域 (0,+∞) (0,+∞)定义域
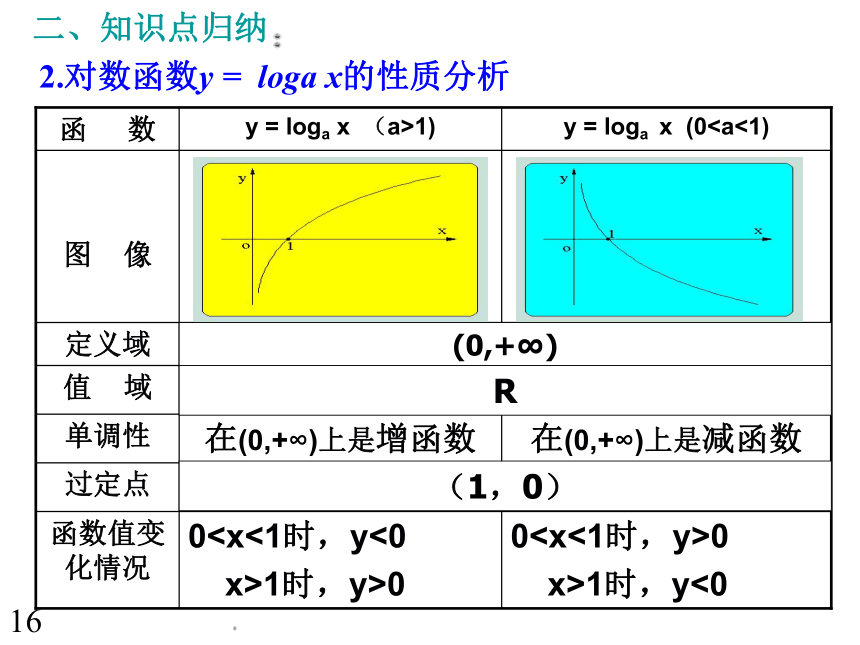
图 像y = loga x (01)函 数(0,+∞)R（1，0）162.对数函数y = loga x的性质分析例1 计算（1） （2） 讲解范例 解 :=5+14=19解 :讲解范例 （3） 解 :=33. y = a x与 y = loga x互为反函数的图像交点 1.求下列函数的定义域：（1）（2）（3）（4）课前热身 P28,练习:3,例1：比较下列各组数中两个值的大小：（1） log 2 7 与 log 3 7解：∵ log 7 3 ＞ log 7 2 ＞0∴ log 2 7 ＞ log 3 7（2） log 0 . 2 0 . 8 与 log 0 . 3 0 . 8解：∵ log 0 . 8 0 . 2 ＞ log 0 . 8 0 . 3且 log 0 . 8 0 . 2 、 log 0 . 8 0 . 3 ＞0∴ log 0 . 2 0 . 8 ＜ log 0 . 3 0 . 80 11xya>1,底数越大，图象越靠近 x 轴0(A)0＜a＜b＜1 (B)0＜b＜a＜1
(C)1＜b＜a (D)0＜b＜1＜a
5.方程loga(x+1)+x2＝2(0＜a＜1)的解的个数是( )
(A)0 (B)1 (C)2 (D)无法确定 返回BC例3 解下列不等式两边取以2为底的对数得(2) 依题意得,所以 x+2 > 27 > 0即 x > 25例2、求函数 y = log 2 ( 1－x 2 ) 的值域和单调区间。解：∵ 1－x 2 ＞0 且 1－x 2 ≤1即 0＜ 1－x 2 ≤1∴ y ≤ 0故 函数的值域为 (－∞，0 )由于此函数的定义域为 (－1 , 1 ) 且 y = log 2 t 在 ( 0 , 1 ) 上是增函数又 t = 1－x 2 (－1 （1）求 f ( x ) 的定义域；解：由题 a x －b x ＞0 得 a x ＞ b x∵ a＞1＞b＞0∴ x ＞0故 f ( x ) 的定义域为 ( 0 , + ∞ )∴ 例3、已知 f ( x ) = lg ( a x －b x ) ( a＞1＞b＞0 )(2)判断 f ( x ) 的单调性。解：设 0＜x 1＜x 2 ＜ + ∞,则 f ( x 1 ) －f ( x 2 ) =∵ a＞1＞b＞0即 f ( x 1 ) －f ( x 2 ) ＜0∴ f ( x 1 ) ＜ f ( x 2 ) 故 f ( x ) 在( 0 , + ∞ ) 上是增函数例3、已知 f ( x ) = lg ( a x －b x ) ( a＞1＞b＞0 )（3）当 a、b 满足什么条件时，f ( x ) 在区间 [ 1 , + ∞) 上恒
为正。解：∵ f ( x ) 在( 0 , + ∞ ) 上是增函数∴ f ( x ) min = f ( 1 ) = lg ( a －b )只要使 lg ( a －b ) ＞ 0就可以了,故满足 a －b ＞1 要使f ( x ) 在区间 [ 1 , + ∞) 上恒为正。1.比较下列各题中两个值的大小：＞＜？ 当a＞1时,函数y=log ax在(0,+∞)上是增函数,
于是 log a5.1＜log a5.9
当0＜a＜1时,函数y=log ax在(0,+∞)上是减函数,
于是 log a5.1＞log a5.9小结1.对数性质
2.对数函数图像和性质