3.3指数函数课件 北师大必修1
图片预览









文档简介
课件43张PPT。§3 指数函数学习导航
学习目标
重点难点
重点:指数函数的图像与性质.
难点:指数函数中底数a的变化对函数值变化的影响.
1.指数函数的概念
函数y=ax(a>0且a≠1,x∈R)叫作指数函
数,在这个函数中,自变量x出现在指数的位置上,底数a是一个大于0且不等于1的常量,函数的定义域是实数集R.
做一做
1.下列函数是指数函数的是( )
A.y=(-3)x B.y=-3x
C.y=32x D.y=2x+1
解析:选C.32x=(32)x=9x是指数函数.
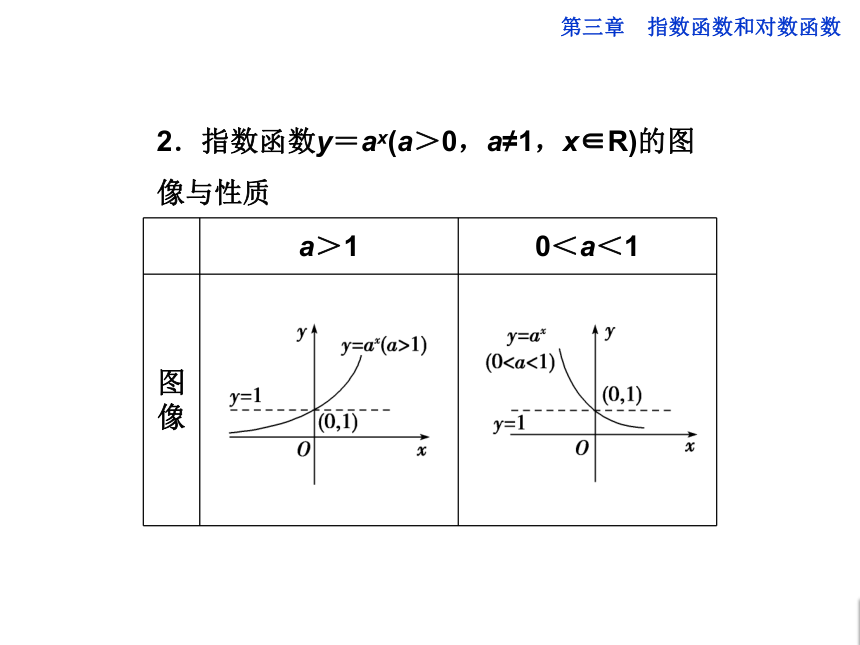
2.指数函数y=ax(a>0,a≠1,x∈R)的图像与性质
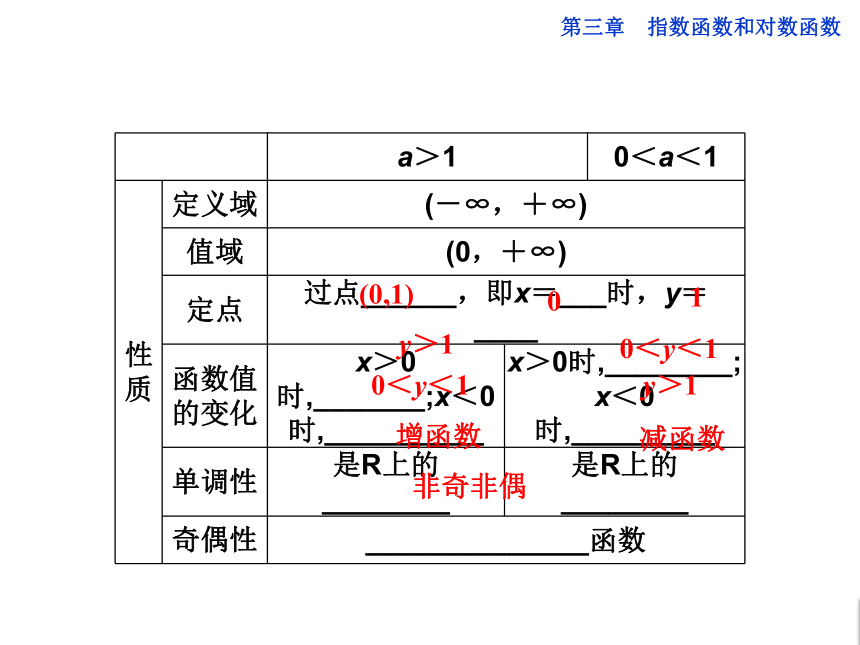
(0,1)01y>10<y<10<y<1y>1增函数减函数非奇非偶做一做
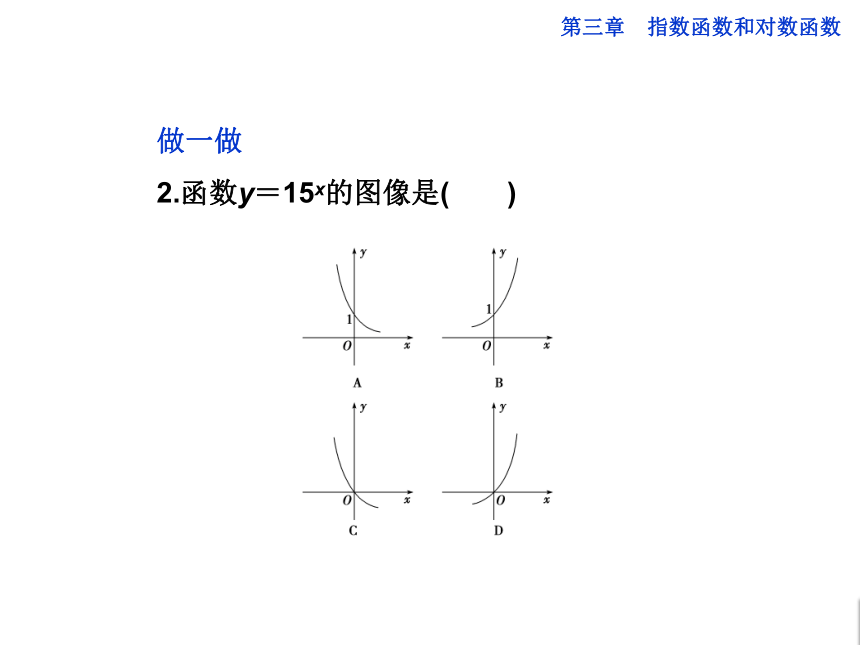
2.函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D想一想题型一 与指数函数相关的定义域、值域问题
求下列函数的定义域和值域:
对于值域问题,一方面要考虑函数的定义域和单调性,另一方面还必须兼顾指数函数的值域是(0,+∞).一般地,对于y=af(x)型函数,建议先求出f(x)的值域A,再画出y=ax(x∈A)的草图和利用函数的单调性,就能很容易求出整个函数的值域.
变式训练题型二 有关指数不等式的求解
画出函数y=|3x-1|的图像,并利用图像回答:k为何值时,方程|3x-1|=k无解?有一解?有两解?
【解】 函数y=|3x-1|的图像如下(图中实线部分).
由图可知,当k<0时,直线y=k与函数y=|3x-1|的图像无交点,即方程|3x-1|=k无解;
当k=0或k≥1时,直线y=k与函数y=|3x-1|的图像有唯一的交点,即方程|3x-1|=k有一解;
当0<k<1时,直线y=k与函数y=|3x-1|的图像有两个不同交点,即方程|3x-1|=k有两解.
【思维总结】 方程根(x)的个数,就是两个函数图像交点的个数.
变式训练题型三 指数函数性质及应用
名师微博
【思维总结】 法一用单调性定义,法二是复合函数法,“同增异减”求值域时易丢掉“y>0”.
题型四 有关指数不等式的求解
【名师点睛】 利用指数函数的单调性解不等式时,需将不等式两边的数凑成底数相同的指数式,并判断底数与1的大小关系.
变式训练
3.比较下列各题中两个数的大小:
(1)1.72.5 ,1.73;(2)2.3-0.28 ,0.67-3.1;(3)a1.3,a2.5(a>0且a≠1).
解:(1)由于1.72.5与1.73的底数都是1.7,故可以构造函数y=1.7x,则函数y=1.7x是R上的增函数,又2.5<3,所以1.72.5<1.73.
(2)由指数函数的性质知:2.3-0.28<2.30=1,0.67-3.1>0.670=1,所以2.3-0.28<0.67-3.1.
(3)当0<a<1时,函数y=ax是R上的减函数,此时a1.3>a2.5;当a>1时,函数y=ax是R上的增函数,此时a1.3<a2.5.
综上所述,当0<a<1时,a1.3>a2.5;当a>1时,a1.3<a2.5.
1.函数y=a2x+2ax-1(a>0,a≠1)在区间
[-1,1]上有最大值14,求a的值.
解:y=(ax)2+2ax-1=(ax+1)2-2,
令ax=t,则y=(t+1)2-2,对称轴为t=-1.
①当a>1时,已知-1≤x≤1,
方法技巧
1.指数幂ax和1的比较:
当x<0,0<a<1或x>0,a>1时,ax>1,即指数x和0比较,底数a和1比较,当不等号的方向相同时,ax大于1,简称为“同大”.
当x<0,a>1或x>0,0<a<1时,0<ax<1,即指数x和0比较,底数a和1比较,当不等号的方向相反(异)时,ax小于1,简称为“异小”.
因此简称为“同大异小”.
2.设a>b>1>c>d>0,则y=ax,y=bx,y=cx,y=dx的图像如图所示,从图中可以看出:在y轴右侧,图像从上到下相应的底数由大变小,在y轴左侧,图像从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.
3.比较指数幂的大小时,通常有以下几种方法:当幂式的底数相同时,则利用指数函数的单调性进行比较,当底数中含有字母时要注意分类;若幂式的底数不同而指数相同时,可以根据指数函数的图像随底数的变化规律,利用图像进行比较;若底数不同且幂指数也不同时,则需要引入中间量进行比较,
中间量可以是幂式,使它与其中一个底数相同而与另外一个指数相同,或用0、1作为中间量.失误防范
1.指数函数y=ax(a>0,a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1.
指数函数解析式的结构的三个特征是判断函数是否为指数函数的三个标准,缺一不可.
学习目标
重点难点
重点:指数函数的图像与性质.
难点:指数函数中底数a的变化对函数值变化的影响.
1.指数函数的概念
函数y=ax(a>0且a≠1,x∈R)叫作指数函
数,在这个函数中,自变量x出现在指数的位置上,底数a是一个大于0且不等于1的常量,函数的定义域是实数集R.
做一做
1.下列函数是指数函数的是( )
A.y=(-3)x B.y=-3x
C.y=32x D.y=2x+1
解析:选C.32x=(32)x=9x是指数函数.
2.指数函数y=ax(a>0,a≠1,x∈R)的图像与性质
(0,1)01y>10<y<10<y<1y>1增函数减函数非奇非偶做一做
2.函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D想一想题型一 与指数函数相关的定义域、值域问题
求下列函数的定义域和值域:
对于值域问题,一方面要考虑函数的定义域和单调性,另一方面还必须兼顾指数函数的值域是(0,+∞).一般地,对于y=af(x)型函数,建议先求出f(x)的值域A,再画出y=ax(x∈A)的草图和利用函数的单调性,就能很容易求出整个函数的值域.
变式训练题型二 有关指数不等式的求解
画出函数y=|3x-1|的图像,并利用图像回答:k为何值时,方程|3x-1|=k无解?有一解?有两解?
【解】 函数y=|3x-1|的图像如下(图中实线部分).
由图可知,当k<0时,直线y=k与函数y=|3x-1|的图像无交点,即方程|3x-1|=k无解;
当k=0或k≥1时,直线y=k与函数y=|3x-1|的图像有唯一的交点,即方程|3x-1|=k有一解;
当0<k<1时,直线y=k与函数y=|3x-1|的图像有两个不同交点,即方程|3x-1|=k有两解.
【思维总结】 方程根(x)的个数,就是两个函数图像交点的个数.
变式训练题型三 指数函数性质及应用
名师微博
【思维总结】 法一用单调性定义,法二是复合函数法,“同增异减”求值域时易丢掉“y>0”.
题型四 有关指数不等式的求解
【名师点睛】 利用指数函数的单调性解不等式时,需将不等式两边的数凑成底数相同的指数式,并判断底数与1的大小关系.
变式训练
3.比较下列各题中两个数的大小:
(1)1.72.5 ,1.73;(2)2.3-0.28 ,0.67-3.1;(3)a1.3,a2.5(a>0且a≠1).
解:(1)由于1.72.5与1.73的底数都是1.7,故可以构造函数y=1.7x,则函数y=1.7x是R上的增函数,又2.5<3,所以1.72.5<1.73.
(2)由指数函数的性质知:2.3-0.28<2.30=1,0.67-3.1>0.670=1,所以2.3-0.28<0.67-3.1.
(3)当0<a<1时,函数y=ax是R上的减函数,此时a1.3>a2.5;当a>1时,函数y=ax是R上的增函数,此时a1.3<a2.5.
综上所述,当0<a<1时,a1.3>a2.5;当a>1时,a1.3<a2.5.
1.函数y=a2x+2ax-1(a>0,a≠1)在区间
[-1,1]上有最大值14,求a的值.
解:y=(ax)2+2ax-1=(ax+1)2-2,
令ax=t,则y=(t+1)2-2,对称轴为t=-1.
①当a>1时,已知-1≤x≤1,
方法技巧
1.指数幂ax和1的比较:
当x<0,0<a<1或x>0,a>1时,ax>1,即指数x和0比较,底数a和1比较,当不等号的方向相同时,ax大于1,简称为“同大”.
当x<0,a>1或x>0,0<a<1时,0<ax<1,即指数x和0比较,底数a和1比较,当不等号的方向相反(异)时,ax小于1,简称为“异小”.
因此简称为“同大异小”.
2.设a>b>1>c>d>0,则y=ax,y=bx,y=cx,y=dx的图像如图所示,从图中可以看出:在y轴右侧,图像从上到下相应的底数由大变小,在y轴左侧,图像从下到上相应的底数由大变小,即无论在y轴的左侧还是右侧,底数按逆时针方向变大.
3.比较指数幂的大小时,通常有以下几种方法:当幂式的底数相同时,则利用指数函数的单调性进行比较,当底数中含有字母时要注意分类;若幂式的底数不同而指数相同时,可以根据指数函数的图像随底数的变化规律,利用图像进行比较;若底数不同且幂指数也不同时,则需要引入中间量进行比较,
中间量可以是幂式,使它与其中一个底数相同而与另外一个指数相同,或用0、1作为中间量.失误防范
1.指数函数y=ax(a>0,a≠1)解析式的结构特征:
①底数:大于零且不等于1的常数;
②指数:自变量x;
③系数:1.
指数函数解析式的结构的三个特征是判断函数是否为指数函数的三个标准,缺一不可.
