3.2指数的扩充及其运算性质课件 北师大必修1
文档属性
| 名称 | 3.2指数的扩充及其运算性质课件 北师大必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-18 15:35:18 | ||
图片预览











文档简介
课件36张PPT。§2 指数扩充及其运算性质
学习导航
学习目标
重点难点
重点:幂的运算性质.
难点:无理数指数幂、分数指数幂的含义.
1.分数指数幂
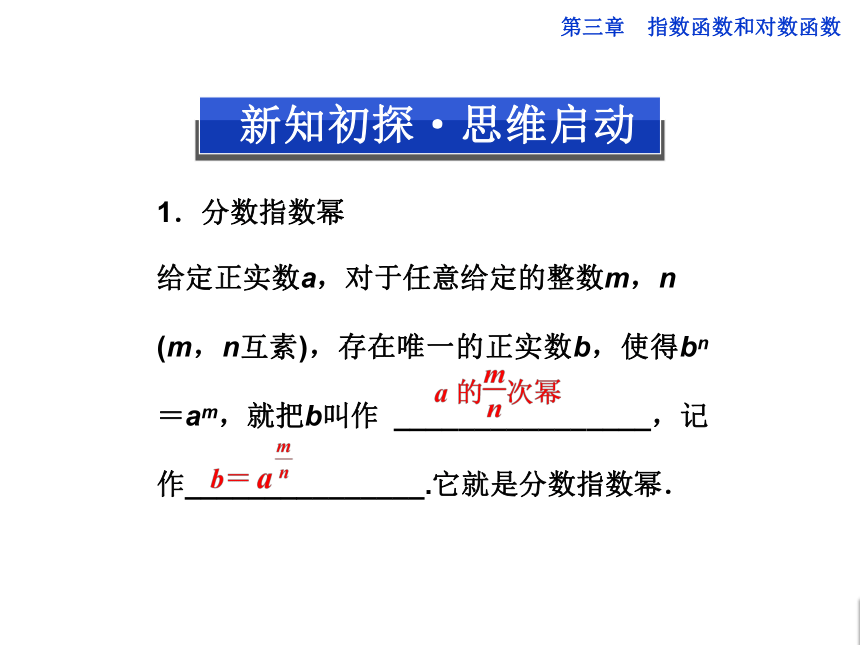
给定正实数a,对于任意给定的整数m,n
(m,n互素),存在唯一的正实数b,使得bn=am,就把b叫作 ________________,记作_______________.它就是分数指数幂.
没有意义0由于有理数分为整数和分数,则引入分数指数幂的概念后,指数概念就实现了由整数指数幂向有理数指数幂的扩充.
想一想做一做 答案:A其中m,n∈N+.
当a>0,b>0时,对任意实数m,n都满足上述性质,上述五条运算性质也可以归纳为三条:
(1)aman=__________;(2)(am)n=_______;(3)(ab)n=__________.
am+namnanbn3.无理数指数幂
对于无理数指数幂,我们可以从有理数指数幂来理解,由于无理数是无限不循环小数,因此可以取无理数的不足近似值和过剩近似值来无限逼近它.
一般来说,无理数指数幂ap(a>0,p是一个无理数)是一个确定的实数.
由于实数分为有理数和无理数,则规定了无理数指数幂后,我们就把指数扩大为全体实数了.
做一做
题型一 分数指数幂与根式的转化
计算下列各式的值:
【思维总结】 解决本题的关键是理解分数指数幂的意义,根式是分数指数幂的另一种形式,将根式化为分数指数幂的形式是计算的前提.
变式训练题型二 指数幂的综合运算
计算下列各式.
【名师点睛】 进行指数运算时,要化负指数为正指数,化根式为分数指数幂,化小数为分数运算,同时还要注意运算顺序问题.
变式训练题型三 有关指数幂的条件求值
【思维总结】 巧妙地换元、整体代换、完全平方公式、立方和公式等是解这类题常用的方法和知识.
方法技巧
1.指数幂的一般运算步骤是:有括号先算括号里的;无括号先做指数运算;负指数幂化为正指数幂的倒数;底数是负数,先确定符号;底数是小数,先要化成分数;底数是带分数,先要化成假分数,然后要尽可能用幂的形式表示,便于用指数运算性质.2.在分数指数幂运算中,既含有分数指数幂,又含有根式,应该把根式统一化为分数指数幂的形式,便于运算,如果根式中根指数不同,也应化为分数指数幂的形式.
失误防范
学习导航
学习目标
重点难点
重点:幂的运算性质.
难点:无理数指数幂、分数指数幂的含义.
1.分数指数幂
给定正实数a,对于任意给定的整数m,n
(m,n互素),存在唯一的正实数b,使得bn=am,就把b叫作 ________________,记作_______________.它就是分数指数幂.
没有意义0由于有理数分为整数和分数,则引入分数指数幂的概念后,指数概念就实现了由整数指数幂向有理数指数幂的扩充.
想一想做一做 答案:A其中m,n∈N+.
当a>0,b>0时,对任意实数m,n都满足上述性质,上述五条运算性质也可以归纳为三条:
(1)aman=__________;(2)(am)n=_______;(3)(ab)n=__________.
am+namnanbn3.无理数指数幂
对于无理数指数幂,我们可以从有理数指数幂来理解,由于无理数是无限不循环小数,因此可以取无理数的不足近似值和过剩近似值来无限逼近它.
一般来说,无理数指数幂ap(a>0,p是一个无理数)是一个确定的实数.
由于实数分为有理数和无理数,则规定了无理数指数幂后,我们就把指数扩大为全体实数了.
做一做
题型一 分数指数幂与根式的转化
计算下列各式的值:
【思维总结】 解决本题的关键是理解分数指数幂的意义,根式是分数指数幂的另一种形式,将根式化为分数指数幂的形式是计算的前提.
变式训练题型二 指数幂的综合运算
计算下列各式.
【名师点睛】 进行指数运算时,要化负指数为正指数,化根式为分数指数幂,化小数为分数运算,同时还要注意运算顺序问题.
变式训练题型三 有关指数幂的条件求值
【思维总结】 巧妙地换元、整体代换、完全平方公式、立方和公式等是解这类题常用的方法和知识.
方法技巧
1.指数幂的一般运算步骤是:有括号先算括号里的;无括号先做指数运算;负指数幂化为正指数幂的倒数;底数是负数,先确定符号;底数是小数,先要化成分数;底数是带分数,先要化成假分数,然后要尽可能用幂的形式表示,便于用指数运算性质.2.在分数指数幂运算中,既含有分数指数幂,又含有根式,应该把根式统一化为分数指数幂的形式,便于运算,如果根式中根指数不同,也应化为分数指数幂的形式.
失误防范
